Towards a dynamical network view of brain ischemia and reperfusion. Part III: therapeutic implications

*Corresponding Author:

Donald J. DeGracia, Ph.D.
Department of Physiology, Wayne State University,4116 Scott Hall
540 East Canfield Ave., Detroit, MI 48201, U.S.A
Phone 313-577-6745
Fax 313-577-5494
E-mail: ddegraci@med.wayne.edu

Abstract

The general failure of neuroprotectants in clinical trials of ischemic stroke points to the possibility of a fundamen-tal blind spot in the current conception of ischemic brain injury, the “ischemic cascade”. This is the third in a se-ries of four papers whose purpose is to work towards a revision of the concept of brain ischemia by applying network concepts to develop a bistable model of brain ischemia. Here the bistable model of brain ischemia is compared to the ischemic cascade concept. The core weakness of the ischemic cascade concept is revealed to be its assumption of superposition, or that the elements of the ischemic cascade can be summed as linearly independent events. This assumption leads to a concept of neuroprotection as a subtraction of ostensibly inde-pendent damage events. The bistable model offers a different concept of neuroprotection where the role of in-dividual molecular pathways decreases in relevance with respect to the efficacy of outcome. Network thinking provides a framework for critical assessment of widely-used preclinical experimental approaches. The impor-tance of allometric scaling is also discussed. We illustrate that the bistable model provides a viable alternative to the ischemic cascade as an explanatory framework and as a guide for therapeutic development.

Keywords

Allometry; bistability; global brain ischemia and reperfusion; neuroprotection; post-ischemic state space

Abbreviations

Akt      pro-survival kinase

CBF      cerebral blood flow

CD      the attractor for cell death

D      delayed neuronal death region of post-ischemic state space

DM      effective total ischemia-induced dam-age

dmi      variable representing a specific damage mechanism

DMSO      dimethyl sulfoxide

H      homeostatic region of post-ischemic state space

HSP70      70kDa inducible heat shock protein

I      the amount of ischemia

IS      the amount of ischemia at the separatrix

N      necrotic region of post-ischemic state space

P      preconditioning region of post-ischemic state space

ROS      reactive oxygen species

S      the attractor for the steady-state pheno-type of a neuron

SR      effective total ischemia-induced stress response capacity

sri      variable representing a specific stress response

TF      transcription factor

TN      threshold of necrosis

Introduction

In this paper we begin to explore implications of the bistable model of brain ischemia, largely by contrast-ing it to the ischemic cascade concept. This will go hand in hand with continued development of the model. Recognizing the complementarity between the pathway and network approaches leads to a dis-cussion of how these may be formally linked. Such considerations lead to a key revelation that superpo-sition appears to be the implicit basis for the ischemic cascade concept, and by extension, the current con-cept of neuroprotection. An alternative view of neu-roprotection that explicitly rejects superposition, based on the bistable model, is then provided. This leads to a more general discussion of how the bista-ble model provides a systematic template for under-standing ischemia-induced cell death. We end this paper by considering the experimental implications of applying network concepts to the problem of brain ischemia. Superposition is also implicit in widely-used preclinical methodologies and serves as a distorting influence on how experimental outcomes are interpreted in terms of causality.

Networks versus pathways: extreme compli-mentarity

The first important fact to note when comparing the traditional molecular pathway view that has given us the “ischemic cascade” to the bistable network model developed here is that, in important regards, they are not mutually exclusive. Choosing viewpoints is not a form of bistability. The approaches are complemen-tary. Each has its strengths which make up for the weaknesses of the other. The pathways approach is like studying individual trees in a forest: it shows us the myriad molecular details up close. The network approach would then be like having a map of the en-tire forest; it shows us the overall system within which the individual details fit. Without some kind of map of the overall process we get into a situation that re-sembles someone trying to deduce the cause of the whole forest by studying only a small patch of trees within the forest. It simply doesn’t make any sense.

What we are really facing here is an issue of balance. The field has developed in an unbalanced fashion by it’s over-focus on molecular details at the expense of a generalized picture of what ischemia is. This is no one’s fault in particular; it is just the course by which the science has evolved. However, as we see ahead, this unbalanced approach has played a signif-icant role in the failure of neuroprotection and it has given us a confused understanding of brain ischemia.

The technical complementarity of the pathways and network approaches is scale. The pathway approach is focused on the scale of individual molecules and their interactions. The network approach as we have applied it here is focused on the scale of the single cell. Networks at other scales can be constructed, such as among brain regions or the behavior of the vascular tree. We have chosen the scale of the indi-vidual cell because it is the individual post-ischemic cell that faces the mutually exclusive decision to live or die.

We stated in the 1st paper that the pathways ap-proach lacks a means to formally integrate the vari-ous pathways, but that the network approach is a formal approach to integrating these. We have now illustrated this by reducing all changes induced in the brain by ischemia to the variables DM and SR. This allows us to study the aggregate (e.g. integrated or total) behavior of the damaging (DM) and protective responses (SR) with no reference to specific details. It is in this fashion that the network model formally integrates the details.

Individual changes and the varaibles dm and sr

It therefore becomes mandatory to ask about the re-lationship between DM and SR as aggregate or total variables, and the individual changes of which each consists. This is a central question with immediate bearing on the question of neuroprotection.

To begin to address this question, let us return to Dr. Wieloch’s sandwich model. While he has been kind enough to grant me permission to use his unpub-lished idea in this work (Tadeusz Wieloch, personal communication), I must add the following disclaimer. Because this model has not been published, there is no source from which to draw upon regarding Dr. Wieloch’s conception of his model. Therefore, it needs to be made perfectly clear that the presenta-tion and interpretation of the sandwich model are solely my own and what is said here should in no way be construed as representing Dr. Wieloch’s view.

Recall the sandwich model envisions stacking the damage mechanisms on top of each other to form a sandwich. The height of each layer, each damage mechanism, reflects the strength or intensity of that specific form of damage. If the height of the whole sandwich passes some threshold height, then cell death ensues. This idea is clearly an attempt to for-mulate how the combined action of the many forms of ischemia-induced damage integrate and contribute in aggregate to cell death. This is indeed a seminal notion. Dr. Wieloch’s sandwich model is the logical predecessor of the bistable network model.

In fact, the sandwich model provides a means to lit-erally calculate DM. Let’s see how this works. For clarity in discussion we now notate any individual damage mechanism in small case letters as dmi. The i subscript is simply a counter, e.g. dm₁, dm₂, dm₃…dmm, saying there are m individual damage mechanisms. According to the sandwich model, DM is the sum of the heights of each individual damage mechanism, where we can take the height to represent the intensity of each individual damage mechanism. Instead of a pictorial of a sandwich, we can now express this as an equation:

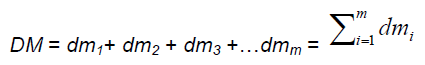
We note the sandwich model does not explicitly ac-count for ischemia-induced stress responses. By analogy, we can do the exact same thing for n indi-vidual stress responses.

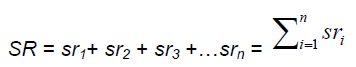
Thereby we arrive at precise relationships between the individual events that make up the molecular pathways of the ischemic cascade and the aggregate variables required for the bistable network model. In both principle and practice, suitable markers for each of the dmi and sri could be determined and measured, and, on some normalized basis, plugged into the above equations to give us real answers for both DM and SR. For example, the amount of some product of lipid peroxidation produced as a function of the amount of ischemia, I, could be one dmi. Other dmi might include (all as functions of I): the increase in cytoplasmic Ca2+, the decrease in endoplasmic reti-culum Ca2+, the amount of proteolysis of specific pro-teins, the degree of calpain I activation, the amount of cytoplasmic cytochrome C, the degree of DNA frag-mentations, and so on. Similarly, specific sri might be: the amount of HSP70 protein, the degree of phos-phorylation of Akt1, the degree of activation of eNOS or the AMP-activated protein kinase, and so on. Clearly this would be a complicated endeavor be-cause the list of dmi and sri will be large, and the task would presuppose having the lists of dmi and sri in hand. Although a huge task, it is, in principle, a doa-ble task.

Thus it seems we have established a concordance between the traditional pathway view of the ischemic cascade and the bistable network view of brain ischemia. But alas, all is not well. The form of the equations above has a name. That name is super-position.

Superposition in brain ischemia studies and neuroprotection

There is one thing about math: it offers lots of possi-bilities. If we can imagine adding the individual dmi or sri, why can’t we instead multiply them? Or maybe they require an integral. Or do they need weighting? Or is there some more complex form of mathematical relationship between them? Do we take each dmi or sri and divide it by the sum of all the others? Or here is a nightmare thought: maybe the form of the rela-tionship changes as a function of where it is at in the state space.

The point being that, while we do truly achieve con-cordance between the pathway and network views by realizing that the individual elements are related somehow to give DM and SR, the fact is we don’t know what the form of that relationship is. Assuming they are to be added in the form shown above is ex-actly that, it is an assumption. Further, it is the as-sumption of superposition. Superposition is the linear summing of independent events. Or said slightly dif-ferently, the net response of two or more independent events is the sum of each individual event (Rodgers et al 1984).

Whether or not it is Dr. Wieloch’s explicit intend, our reading of the sandwich model is that it reveals the fact that the assumption of superposition permeates the field. First each individual event is isolated from all others on its own separate layer in the sandwich, or as its own term in the equation; this reveals the assumption that the events are independent of each other, e.g. do not interact. Then these are simply added together. Adding independent things is super-position. Superposition is the exact opposite of a network view where each node is directly dependent on its input nodes, and indirectly dependent on the state of all the nodes. In fact, superposition and net-work models are mutually exclusive. Nodes are simply not independent in a network. Conversely, a collection of independent things cannot form a net-work.

Thus, there is a double edge to the sandwich model. On one hand, it provides the seminal insight that the individual events induced by ischemia can somehow be aggregated or related. On the other hand, in the specific form it has been presented, it assumes that the form of that relationship is superposition. In the 4th paper we present the idea that the individual dmi and sri are related as the nodes of the network under-lying the post-ischemic state space. The purpose of much of the remainder of the present paper is to fo-cus on the implications that superposition seems to permeate the field.

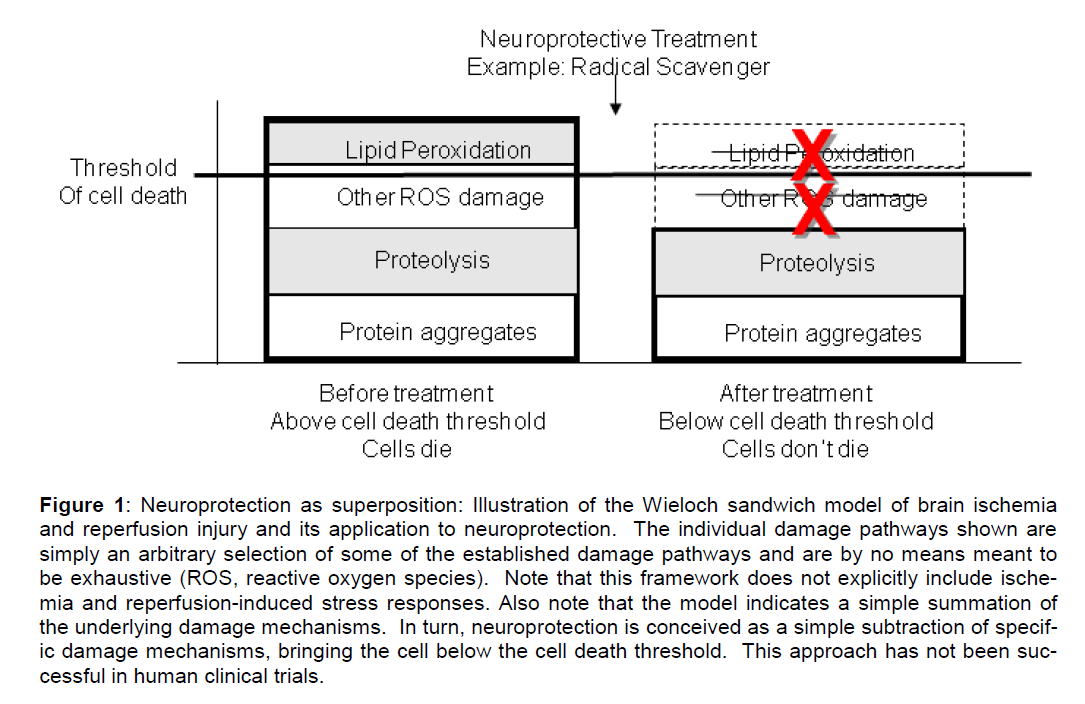
Perhaps the most important implication is that the sandwich model reveals how superposition is the hidden assumption of the current conception of neu-roprotection. What is the widely held idea of neuro-protection? We administer a drug that is supposed to inhibit one or the other of the many identified damage pathways. This is effectively an attempt to subtract that damage mechanism from the mix. It amounts to attempting to remove one or more of the dmi terms from the linear sum. This is illustrated using the sandwich model in Figure 1. Here a radical scaven-ger is given to eliminate reactive oxygen species (maybe NXY-059?). The expectation is that by re-ducing (e.g. subtracting) a couple of the assumed independent damage components (e.g. dmi) this will bring the cells below the cell death threshold, and thereby salvage them.

Figure 1: Neuroprotection as superposition: Illustration of the Wieloch sandwich model of brain ischemia and reperfusion injury and its application to neuroprotection. The individual damage pathways shown are simply an arbitrary selection of some of the established damage pathways and are by no means meant to be exhaustive (ROS, reactive oxygen species). Note that this framework does not explicitly include ische-mia and reperfusion-induced stress responses. Also note that the model indicates a simple summation of the underlying damage mechanisms. In turn, neuroprotection is conceived as a simple subtraction of specif-ic damage mechanisms, bringing the cell below the cell death threshold. This approach has not been suc-cessful in human clinical trials.

What’s clear from the clinical trials is that subtraction approach, implicitly based on superposition, has not worked. Some authors question if neuroprotection is even possible in principle (Röther 2008). We do not here pretend to be able to magically answer why neu-roprotection has completely failed in human clinical trials but offer some thoughts grounded in the net-work view, hopefully novel. While the refinement of clinical and preclinical methodologies seems a rea-sonable step towards assuaging the problem, it is not without pitfalls. In a subsequent section we offer a critical analysis of preclinical methodologies, them-selves implicitly permeated by the assumption of su-perposition. We now address neuroprotection and cell death from a network point of view. We begin by way of a brief detour into allometry, a critical quanti-tative consideration that needs to be integrated into our thinking, whether or not one accepts the premise of network thinking.

Pay attention to allometry!!!

A PubMed search of “allometry” and “stroke”/“brain ischemia”/“etc.” gives one paper pertinent to brain ischemia. This is Curry (2003) where he makes the case for the importance of allometric scaling in drug delivery and the allometrics of comparing the ischem-ic cascade amongst organisms. That only one paper directly addresses this issue says much about the extent of quantitative thinking in our field. What is perhaps worse, Scopus citation tracker reveals only 15 citations of this paper for which 8 are specific to brain ischemia. To put this in perspective, a simple PubMed search of “apoptosis brain ischemia” gives 2,396 papers (as I write in late February, 2010).

Allometry or allometric scaling is the study of the scaling and relative proportions (sizes, weights, rates, etc) of the parts and functions of different species or individuals within a species. This area has recently been championed and perhaps even revitalized by Geoff West (Brown 2000). One of the significant con-tributors to the failure of neuroprotection could be due to not adequately taking allometric effects into ac-count. An obvious example is drug dosing. If some drug is effective in rodents at X mg/kg, and it is simp-ly scaled by body weight (kg) and given to humans, one is assuming a scaling of the drug effect as a li-near function of body weight. The study of allometry reveals that most such scaling generally obeys power laws that are not linear.

But allometry is not only directly applicable to scaling drug doses; it also involves understanding the rela-tive proportions of parts and functions, which is ex-pected to be crucial in comparing different species. A relevant example can be found in a report from Bois-sel’s group in France (of whom more is spoken in the 4th paper). This group performed computer simula-tions modeling the differences in the amount of white matter and glia between rodents and humans and how simulated drugs would behave in these different milieus (Dronne et al 2007). The impetus here was clear: human strokes often involve white matter le-sions, which are comparably rarer in rodent models of brain ischemia. Their simulations indeed showed different responses of simulated drug treatments be-tween the in silico rodent and human brains. The Dronne et al 2007 computer study shows, in effect, that taking the allometric scaling of white matter and glia into explicit account makes a difference in drug efficacy.

One place where allometry would be relevant in the context of the bistable model is in comparing post-ischemic state spaces amongst neuron subtypes in a species (e.g. as illustrated in Figure 4B of the 2nd pa-per of this series), or in comparing neuronal subtype state spaces amongst species. Some specific allo-metric relationship is expected from such compari-sons. Understanding the allometric relationships be-tween different neuronal post-ischemic state spaces is potentially a very important factor for developing therapeutics because it will allow correct scaling from preclinical animal models to human patients.

Therefore, it needs to be strongly highlighted that comparing results between humans and animals re-quires taking into account all the relevant allometric scaling. If this is not done, failure is almost guaran-teed. Given the central role of animal models in prec-linical testing of neuroprotective agents, and quite independent from the application of network thinking to the problem of brain ischemia, we strongly urge that an effort be undertaken to integrate allometry into all studies of brain ischemia and reperfusion.

No drug is better than the next

Returning back to neuroprotection, we again consider the quote by O’Collins et al (2006) that opened the 1st paper. We repeat only the relevant bit: “No particular drug mechanism distinguished itself on the basis of superior efficacy in animal models of focal ischemia.” This same general sentiment also applies to pharma-cologic interventions following global cerebral ische-mia (Weigl et al 2005; Fukuda and Warner 2007). The bistable model offers a surprising take on this observation. To make our point, however, we revert briefly, and for the last time, to some additional de-tails about differentiation.

We discussed the GATA1/PU.1 competition in the 2nd paper. One question we did not consider was what determines which transcription factor (TF) is at a higher amount in the progenitor cell. Physiologically (e.g. in vivo) this involves growth factor or mitogenic signaling pathways (Chiba et al 1991; Enver et al 1998). The differential expression of the TFs is con-trolled by the ligands in the cell’s environment. What is amazing is that seemingly unrelated stimuli can substitute for the growth factor signaling pathways. We saw in the 1st paper that DMSO can be used to induce differentiation (Santos et al 2003), but DMSO is just a solvent. It is also possible to trigger differen-tiation by mechanical deformation of the progenitor cells (Huang and Ingber 2000). In my own lab, we routinely differentiate NB104 neuroblastoma cells using a non-hydrolyzable analogue of cAMP (Kumar et al 2003) How can such a diverse array of stimuli – ligands, 2nd messenger analogs, solvents, mechan-ical force – control transcription with any specificity? We note in passing that this situation is reminiscent of how a diverse array of stimuli can induce the heat shock response: heat, heavy metals, osmotic shock, ethanol, ischemia, etc. (Lindquist 1986).

While some research in this area seeks to show that these stimuli converge to the same intracellular pathways, existing evidence by no means conclusive-ly supports such a view (Chao 1992; Huang and In-gber 2000). The network view offers a completely different explanation. We saw in the 1st paper that both DMSO and retinoic acid could induce the same differentiated phenotype by traversing different trajec-tories in the state space, that nonetheless converged to the same attractor (Huang et al 2005). Either sti-mulus provided a perturbation, a “kick” if you will, to the system, inducing movement of the network confi-guration out of one attractor and in the general direc-tion towards another.

The generalization here is: because the phenotypic transformation is viewed as movement from one at-tractor to another, the specific details of the initiating stimulus and its trajectory are less important than the final outcome. Different stimuli lead to the same out-come, with the main difference between stimuli being the trajectory taken towards the final result. However, the specific details resulting from following a specific trajectory are simply less important than the fact that the trajectory moves inevitably towards a specific at-tractor (phenotype). By such logic we can explain why no particular drug has shown superior efficacy in animal studies of brain ischemia and reperfusion.

An alternative interpretation of what neuropro-tection is

In a relatively recent review of neuroprotection, My-ron Ginsberg (2008) frankly discussed the “every-thing works in animals” issue raised in O’Collins et al (2006). The conflict boils down to the fact that we are faced with what appear to be two contradictory piec-es of evidence:

1. The Ginsberg point: There is seemingly some degree of specificity to neuroprotective drugs. That is, everything doesn’t work as a neuroprotectant.

2. The O’Collins et al (2006) point: The ischem-ic cascade concept indicates certain thera-pies should be highly effective (e.g. gluta-mate antagonism, calcium channel blockers, free radical scavengers, anti-apoptotic agents). However, no agent that does work as a neuroprotectant shows superior efficacy over any other agent that works. Thus, any agent might as well work since our expecta-tion of what should be most efficacious is constantly foiled. In short, there seems to be some basic flaw in the idea that specificity of drug action relates to efficacy in neuroprotec-tion.

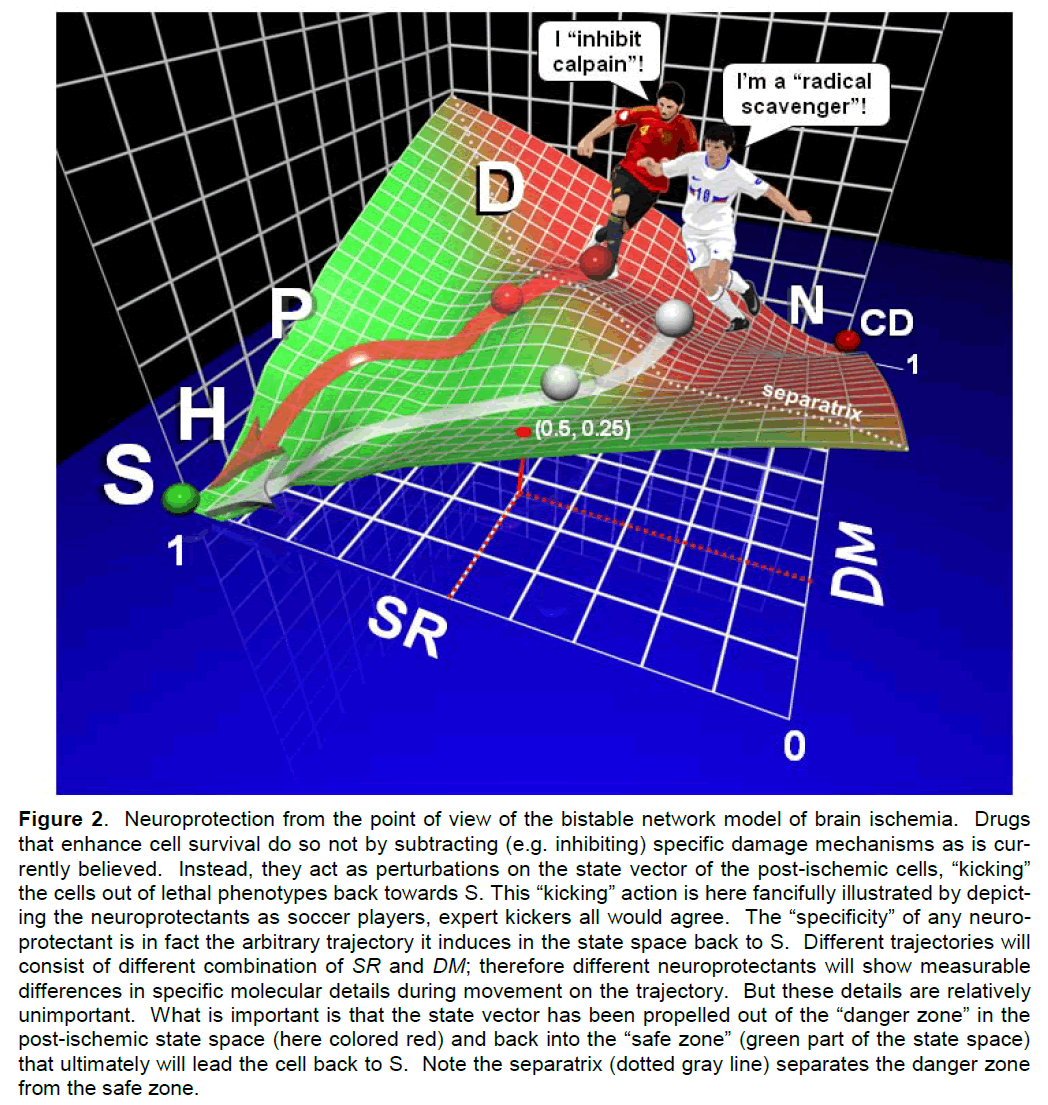
We suggest the resolution of this apparent conflict is exactly analogous to the differentiation examples cited above. What works does so not because it is subtracting out damage as is commonly thought (as illustrated in Figure 1). Neuroprotection works because the drug treatments are a perturbation in the post-ischemic state space that push or “kick” the cells back towards S. One must imagine the network con-figuration (e.g. our ubiquitous marble) poised in some lethal part of the post-ischemic state space. The le-thal area of the post-ischemic state space is that to the right of the separatrix, which we could call the “danger zone,” and is painted red in Figure 2. The “danger zone” is the basin of attraction of the attrac-tor CD in the post-ischemic state space.

Figure 2. Neuroprotection from the point of view of the bistable network model of brain ischemia. Drugs that enhance cell survival do so not by subtracting (e.g. inhibiting) specific damage mechanisms as is cur-rently believed. Instead, they act as perturbations on the state vector of the post-ischemic cells, “kicking” the cells out of lethal phenotypes back towards S. This “kicking” action is here fancifully illustrated by depict-ing the neuroprotectants as soccer players, expert kickers all would agree. The “specificity” of any neuro-protectant is in fact the arbitrary trajectory it induces in the state space back to S. Different trajectories will consist of different combination of SR and DM; therefore different neuroprotectants will show measurable differences in specific molecular details during movement on the trajectory. But these details are relatively unimportant. What is important is that the state vector has been propelled out of the “danger zone” in the post-ischemic state space (here colored red) and back into the “safe zone” (green part of the state space) that ultimately will lead the cell back to S. Note the separatrix (dotted gray line) separates the danger zone from the safe zone.

A neuroprotective drug is then one that serves to “kick” the configuration out of the “danger zone” and back into the basin of attraction of S. The basin of attraction of S is to the left of the separatrix and we call it the “safe zone” and paint it green in Figure 2. Drugs that enhance cell death “kick” (e.g. accelerate) the cell’s descent to CD. Those drugs that have no effect simply don’t exert any “kick” in the post-ischemic state space that makes a difference for out-come. Figure 2 illustrates the bistable model-derived view of neuroprotection in perhaps a rather fanciful way, which nonetheless emphasizes the idea of “kick.” Figures 1 and 2 starkly contrast neuroprotection as superposition, or neuroprotection in a network, re-spectively.

The so-called “specificity” of each neuroprotectant results not because it “specifically” inhibits some arbi-trary damage pathway X, but because it traverses a trajectory back to S different from some other drug Y. It may happen that the trajectory followed after drug X treatment does involve some degree of suppres-sion of damage pathway X, but maybe not. It doesn’t really matter. All that matters is that the drugs that work push the system through some arbitrary trajec-tory to the “safe zone”, and hence ultimately to S. The details of the trajectory are relatively unimportant compared to the final outcome.

We want to clarify in passing that by calling a neuro-protectant-induced trajectory “arbitrary”, we are not saying a drug will produce arbitrary changes in the post-ischemic brain. We use to the term “arbitrary” to refer to the fact that there are arbitrarily many possi-ble trajectories back to S on the state space land-scape, none any better than the other; they all lead back to S. Thus, each drug will elicit its own unique trajectory (or some related range of them), and the-reby produce relatively reproducible changes in terms of specific molecular pathways.

While network thinking tells us that the details of indi-vidual trajectories are less important than the final outcome, we still take a moment to discuss the phys-ical interpretation of a drug-induced trajectory. To understand a trajectory means understanding a sin-gle point in the state space since the trajectory is just a set of points linked on the state space surface. We discussed this issue in the 2nd paper and now revisit it here.

Looking at Figure 2, a point in the post-ischemic state space can be seen to be some combination of DM and SR in different proportions. We can also see in Figure 2 that the ranges of DM and SR each go from 0 to 1. These ranges imply two things: (1) that we can empirically measure DM and SR, and (2) that these measures can be put on a normalized basis so they can be directly compared. Assuming these to be true for argument’s sake, we can ask what a single point represents. The separatrix is the line where, for each point, DM = SR. In the “safe zone” SR > DM, and in the “danger zone” DM > SR. If we notate a point on the state space surface as (SR, DM), then examples of “safe zone” points would be (1, 0) (this is the at-tractor S), (0.9, 0.5), (0.2, 0.05), and so on. “Danger zone” points would include (0, 1) (attractor CD), (0.5, 0.75), (0.25, 0.35) and so on. Consider the point (0.5, 0.25). This point is marked in Figure 2 and can be seen to be in the “safe zone” on the P-D boundary. What this point means quantitatively is that the total induced stress response capacity (SR) is exactly twice the amount of total damage (DM). In this sense, each point on the state space landscape represents different proportions of DM and SR.

But DM and SR in turn are aggregates of many dmi and sri. As discussed above, we do not yet know the form of the relation between DM/SR and the many dmi/sri. This issue speaks to the form of the network architecture linking the many dmi/sri (a topic dis-cussed in the 4th paper). However, in spite of know-ing neither the network architecture nor the specific mathematical relationship between DM/dmi and SR/sri, we can still make statements about the physi-cal meaning of a point in the state space. Specifically, we can infer that a point must be some pattern of ex-pression of many specific dmi and sri in proportions reflecting their location on the state space.

Physically, a state space point corresponds to distinct patterns of many specific molecular events/pathways, some of which harm the cell (dmi) and some of which help the cell (sri). An adjacent point would be ex-pected to be a minor variation of its neighboring points. Two points separated by a significant dis-tance on the state space surface would represent very different patterns of specific dmi and sri. Not all state space points will be physically realistic. Recall the GATA1/PU.1 example from the 2nd paper. The point (1,1), where GATA1 and PU.1 are both maximal, is probabilistically very unlikely because each inhibits the other. The same would be true for the point (1,1) with DM and SR in the post-ischemic state space. But in the context of such considerations, generally a point in the post-ischemic state space will correspond to some pattern of expression of molecular damage and stress response events in the cell.

As the state vector moves from point to point gene-rating the trajectory, the pattern of underlying specific physical events would transform. In a cell death sce-nario (e.g. a trajectory towards CD), the damage events (dmi) would increase and the stress response events (sri) would decrease. For a neuroprotectant-induced trajectory (e.g. from the “danger zone” and back towards S), the dmi would gradually disappear and the sri would change in such a way to repair the cell, which amounts to resetting it to the S phenotype.

These ideas can be used to reconcile the fact that some drugs work, but none of them show any real differences in terms of superiority of efficacy. The bistable model gives rise to three classes of drug ef-fect in the post-ischemic brain: “towards S” drugs, “towards CD” drugs and no effect. Clearly then, not all drugs work, specificity, in the sense of being a neuroprotectant or not, is present, and Dr. Ginsberg is correct.

However, no drug shows superior efficacy because the neuroprotective effect is not due to a simple sub-traction of one specific form of damage. That is, spe-cificity in terms of a drug being specific for some par-ticular damage mechanism, is not what is going on from the state space point of view. Instead, all neu-roprotective drugs move the cell through points in a multi-dimensional space where each point is a com-bination in different proportions of all the ischemia-induced damage mechanisms (dmi) and stress res-ponses (sri), at various stages in their time courses of expression. According to the bistable model, there is no magical cell death pathway X, which if inhibited by a neuroprotectant, would magically salvage all the neurons.

Hence the intuition expressed in O’Collins et al (2006) is also correct: there is a flaw in linking neuroprotec-tive efficacy to the presumed “specificity” of drug X acting on damage pathway X. That flaw is the as-sumption of superposition, or that drug X simply sub-tracts damage pathway X. The idea of drug “specific-ity” is lost to a large extent in a network context, but so too is the concept of an “off-target” or a “nonspe-cific” drug effect, the latter being the evil twin of the former. In fact, both the so-called “specificity” and the “off-target” or “nonspecific” effects together reflect the action of the agent on the network as a whole, an issue we return to in the final section.

Neuroprotectants as perturbations in the post-ischemic state space

Briefly we here try to sharpen the concept of “kick”. For lack of a better term, we retain the word “kick” because it is at least descriptive. At the risk of sounding glib by retaining the term, it needs to be strongly emphasized that this is unquestionably the most important concept to derive from our bistable model because it provides a new way to conceptual-ize neuroprotection. We do not pretend to have an-swers here, only questions.

The idea of the “kick” of a neuroprotectant is related to the question of effect size: e.g. drug X salvages 20% but drug Y salvages 50%. There are many factors that will bear on effect size, many quite pedestrian and we do not try to consider all of them here. Pede-strian considerations are of the type that drug Y has better brain penetration or gets into cells better. A less entertained possibility is that effect size differ-ences aren’t real and are merely statistical artifacts and no neuroprotectant really is better than any other neuroprotectant. While some might find the sugges-tion contentious because it suggests methodological weakness, it is something we should take seriously in the present context. If effect size differences are a statistical artifact, but effect size itself is not zero (e.g. is some constant percent), this would imply all neuro-protective agents exert the same intensity of “kick” in the post-ischemic state space. On the other hand, if effect size differences are real, it would indicate that different agents can induce different intensities of “kicks”. Given the present way outcome data is col-lected and interpreted, it is virtually impossible to even make an educated guess from the existent data whether different neuroprotective agents exert differ-ent intensities of “kick”. There is too much variation in models, routes of administration, specifics related to the drugs themselves, and other such factors to even find firm footing. Further, when thinking about “kick” intensity, one must consider the starting point at which it is applied. A drug administered to a brain right below TN will need to exert a stronger “kick” to get the cells back over the separatrix than a drug administered to a brain that has experienced a lesser amount of lethal ischemia.

The above considerations offer some small insight into why have neuroprotectants been effective in ro-dents (or other nonhuman mammals) but not in hu-mans. Neuroprotectants that are effective in nonhu-mans produce some amount of “kick” to move the system to S. It is possible that linearly scaling up a drug dose by body weight does not result in the same amount of “kick” in the human brain. That is, we come back to allometry. This is the same argument used above in reference to drug doses, but instead of thinking of the drug effect as inhibiting (subtracting) pathway X, we now think in terms of the effective “kick” of the drug as a perturbation in the post-ischemic state space.

While we here use the term “kick” to keep the con-cept digestible, the concept refers to the action of a neuroprotective agent in the post-ischemic state space. Thinking of the neuroprotectant as exerting a “force” by which to move the state vector (e.g. as a “kick”) is one possible means of doing so. However, as we saw in the case of differentiation, it is possible for a bifurcation to alter the shape of a state space. It is therefore possible that neuroprotectants act as “bi-furcation agents” by changing the shape of the post-ischemic landscape in such a way as to make it easi-er for the state vector to return to the S configuration.Some neuroprotectants may propel the system to S without changing the state space landscape; others may change the shape of the state space landscape. Some drugs might even do both: change the shape of the landscape and provide a “force” sending the state vector back to S.

Whatever the case may be, the bistable model dis-tinctly predicts that such a “kick” should be asso-ciated with any drug treatment. Further it predicts two specific modes of action of a “kick”: as a force or a shape change in the state space. It also predicts that “kicks” should have different intensities insofar as the state space embodies the concept of a distance over which the “kick” must move the state vector. Howev-er, to go beyond the issue as discussed here, which is purely theoretical, some measure of this “kick” needs to be devised. With such a measure one could determine if “kicks” can have variable intensity, and importantly determine the allometric scaling of the “kick” effect between species. Following such a program may get us closer to an effective neuropro-tectant in humans.

Further thoughts on clinical issues and cell death

Having clarified what it means to prevent cell death in the bistable model, we discuss here just what it is we are trying to prevent. In this section we link therapeu-tics to the two modes of cell death in the bistable model, and discuss forms of cell death as relates to concepts of causation.

Therapeutic Modalities and the Bistable Model. The first mode of cell death is that which occurs during ischemia. The bistable model unambiguously states that cells that experience N levels of ischemia will die. That is, passing TN = cell dead. The only way to pre-vent the N phenotype is to prevent cells from passing TN in the first place. For the majority of clinically rele-vant situations, it is unlikely a drug will ever be effec-tive in moving cells out of the N phenotype. This is simply an issue of time: the cells will die before a drug can act. Thus, the N phenotype is ill-suited as a target for neuroprotection. This underscores the importance of and need to continue to develop effec-tive reperfusion or recanilization therapies (Molina and Alvarez-Sabín 2009), what we have elsewhere called “ischemia reduction” techniques (DeGracia, 2008). In the context of the bistable model, these should indeed be collectively referred to as “ischemia reduction” techniques. Their main functional effect is to reduce the amount of ischemia such that cells never experience I > T_N.

The bistable model allows us to make the precise statement that the appropriate targets for neuropro-tective treatments are cells that die during reperfu-sion, where time is a considerably less limiting factor. Such cell death occurs over the range IS < I < TN, and constitutes the lethal D phenotype. As Figure 2 makes plain, an effective neuroprotectant will “kick” the cell out of the lethal D phenotype and back into the “safe zone,” where the cells will inevitably decay back to S.

However, when we consider neuroprotection over the lethal D range, one must ask: does DND manifest identically over this entire range? This seems highly unlikely. DM increases and SR decreases across this range (e.g. Figure 6, 2nd paper). The D pheno-types therefore are expected to constitute a set of different, but related phenotypes, all characterized by death during reperfusion. There may be a few dis-creet phenotypes, and therefore a series. Or the D phenotypes may consist of graded changes across this range, creating a continuum of DND phenotypes. These possibilities can only be resolved experimen-tally, but the present model clearly predicts them, and provides a systematic basis for understanding them.

The possibility that the D phenotype is not a singular entity would be important for systematically develop-ing neuroprotective treatments. The bistable model predicts that the closer a D phenotype is to TN, the faster it will die during reperfusion. Therefore, the notion of the “kick” intensity of a neuroprotectant comes into play. A stronger “kick” will be required to prevent cell death in a D phenotype closer to TN than one closer to IS.

Types of ischemia-induced cell death. We introduced the idea in the 2nd paper that the bistable model pro-vides an alternate view of cell death causation. Here we elaborate on these ideas in relation to contempo-rary notions of ischemia-induced cell death.

At present, ischemia-induced cell death is conceptua-lized by most of the community as either necrosis or apoptosis. This distinction stems from the apparently straightforward recognition that cell death can be in-duced either via extrinsic insult (necrotic) or via inter-nal, active genetic programs (apoptosis). However, as Martin et al (1998) point out, this binary distinction fails to account for cell death forms that are apparent hybrids, including those in the brain during or after ischemia where markers of apoptosis and necrosis can co-occur (Petito et al 1997; Lipton 1999; MacMa-nus and Buchan 2000; Yakovlev and Faden 2004; Sun et al 2009). Thereby concepts of an apoptosis-necrosis continuum have been offered to account for hybrid cell death phenotypes. While these provide useful classification schemes and help organize ob-servations, they also suffer weakness, two of which we now discuss.

First, hybrid cell death classification schemes are generally qualitative, providing checklists of features distinguishing one category from another (e.g. Portera-Cailliau et al 1997; Yakovlev and Faden 2004; Kroemer et al 2009; Sun et al 2009) These systems tend to lack formal, systematic (e.g. read “mathemat-ical”) bases, although there are exceptions (Nicotera et al 1999).

Second, as touched on briefly in the 1st paper, the contemporary view of cell death tacitly assigns an essentially passive role to the injured cells. The idea seems to be that the ischemic insult triggers a set of processes that simply kill the cell, whether by necro-sis or apoptosis. This logic is clearly true in general for any very intense insult that immediately destroys cells. However, for lesser intensity insults in which cell death evolves over time, (e.g. delayed forms of ischemia-induced cell death) the logic is not so strong. With delayed forms of cell death, we must contort ourselves into some concept of programmed cell death as the effective cause, if we tacitly commit to the idea that the cell is powerless to combat the damage. Taken to its extreme, a “passive” view of cell death would completely ignore the cell’s ability to “fight back.”

The bistable model is designed, at least in part, to compensate for these weaknesses. First, it is syste-matic. The scale of I systematically links the degree of the insult to cell death forms. Second, cell death is explicitly the result of the competition between dam-age (DM) and the cell’s ability to combat this damage (SR). Finally, linking DM and SR to their respective dmi and sri link systematic changes in the post-ischemic state space to the type of qualitative changes in molecular pathways or cell morphology that currently characterize the empirical content of the field. The bistable model offers a systematic template by which to approach to the issue of the types of cell death following ischemia that is different from, but well able to encompass, the standard apop-tosis/necrosis framework, where the latter are seen as some of the dmi contributing to DM.

The bistable model allows us to clarify the possible role of both necrotic and apoptotic pathways in ischemia-induced cell death. The points in the state space are every possible combination of different proportions of dmi and sri. We therefore expect some dmi points to have a high proportion of pathways that would be considered “necrotic”. Other dmi points would contain high proportions of pathways consi-dered “apoptotic”. Still other dmi would contain dif-ferent mixes of necrotic and apoptotic pathways, in all conceivable proportions. Thus, the bistable model is intrinsically a hybrid model, but not exclusively so. But most important, it does not conceptualize cell death as being caused by necrotic or apoptotic path-ways. These are simply potential dmi; in other words, specific network nodes, to be found on some of the arbitrary trajectories to CD.

In terms of causation, cell death during N and D are both caused by the same factor: DM > SR. Or said in a nonmathematical way, cell death is caused by the fact that the cell is incapable of coping with the dam-age. Now, the underlying reasons for DM being greater than SR are different in D and N, hence two general modes. As discussed in the 2nd paper, time considerations allow us to infer that kinetic factors underlie cell death in N, whereas thermodynamic fac-tors underlie cell death in D. The factors underlying cell death in N, that the kinetics of damage over-whelms the cell’s ability to respond, are most similar to the current “passive” views of cell death. But even then, the small contribution of SR is explicitly recog-nized in the bistable model.

These notions perhaps appear foreign because they are independent of any specific pathways that may make up the underlying network nodes. As stated above, there is no magic molecular pathway X that causes cell death in the bistable model. The current expectation for discovering the cause of cell death after brain ischemia is highly conditioned on the pre-mise that specific molecular pathways will be identi-fied as the effective cause of cell death. This expec-tation obviously stems from the dominance of path-ways thinking in general. Lacking a systematic un-derstanding of pathway interactions, the default fall-back position is superposition. We now turn our at-tention to how the expectation of discovering the magic cell death pathway X has affected experimen-tal designs and their consequent interpretation of what constitutes causation in the field.

Improving preclinical methodology: banish superposition

Closely related to the failure of neuroprotection is the decision of what to take to clinical trials in the first place. Such decisions stem from preclinical studies showing some significant effect of drug X on post-ischemic outcome in experimental animals. Thus, there is active movement to improve preclinical me-thodologies (Dirnagl 2006; Fisher et al 2009). In the abstract, seeking methodological improvements is very important and legitimate. However, measuring brain temperature to six significant figures is not likely to help us much. The tools we use to do experiments are themselves grounded in theories of how the tools work. It is not constructive to merely attempt to im-prove methodology without questioning the underly-ing assumptions behind the tools themselves. In fact, we stand the chance of foiling our aims if we inadver-tently use the tools incorrectly. What we want to dis-cuss here are the common assumptions that appear to underlie the preclinical testing of neuroprotective agents. There are very serious problems on this front which the present network view brings to light. In a nutshell, the currently accepted idea of “causality” in brain ischemia studies itself seems to be predicated on the assumption of superposition. This is the un-derlying implication of the expectation that magical cell death pathway X will eventually be discovered.

The Plus/Minus Strategy. We can perhaps best de-scribe the main method for claiming to determine causality in post-ischemic death by the term “plus/minus strategy”. The plus/minus strategy is both an algorithm for designing experiments and the widely accepted means of establishing causality in brain I/R studies. In the latter sense it is also the most widely used theoretical tool in the field: if a re-sult passes the experimental algorithm, it gets added into the “ischemic cascade”, thereby expanding the “theory” of brain ischemia. The plus/minus strategy has the following form:

1) Hypothesize that factor X contributes to cell death.

2) Overexpress/activate factor X (the “plus”) and count increase in cell death.

3) Knockdown/inhibit factor X (the “minus”) and count decrease in cell death.

4) Express changes as a percentage from untreated cell death. If this clears statis-tically, one claims to have found a “cause” of cell death.

5) If factor X is hypothesized to protect against cell death, reverse expected di-rections in steps 2 and 3.

Prior to modern molecular methods this algorithm was implemented via pharmacologic means, using “specific” inhibitors or activators. Newer molecular methods allow overexpression or knockout of specific proteins to effect the plus and minus operations.

Generally speaking, application of this algorithm has routinely resulted in roughly a 20%-30% decrease in cell death after brain I/R for a very wide variety of damage mechanisms (O’Collins et al 2006). It is this generally nonspecific outcome for such a large varie-ty of agents that led O’Collins et al (2006) to question the value of assuming that apparent drug specificity relates to neuroprotective efficacy. We take a differ-ent tact at this point in the discussion and use this 20%-30% fact as a means to question “business as usual” (Donnan 2008).

Let us take the general 20%-30% result at face value. Only 3 to 5 independent things can each have a 20%-30% effect. Table 4 in O’Collins et al (2006) breaks neuroprotectants into 14 categories. Figure 3 in Ginsburg (2008) lists 49 targets of neuroprotection. Let us be conservative and say that a dozen targets of neuroprotection have been unambiguously identi-fied. If each of these dozen damage mechanisms is assumed to be independent, and each contributed say exactly 20% to cell death, then we end up with 240%. Somehow we end up with 140% more cells than with which we started. We can call this the “240% inconsistency” and it explicitly follows from assuming that the separate damage mechanisms are indepen-dent.

The bistable model offers the alternative interpreta-tion given above that can indeed explain this see-mingly inconsistent result. The 20%-30% represents the “kick” of a particular agent (e.g. the number of cells that can be sent from the danger zone to the safe zone), not the subtraction of an assumed inde-pendent damage mechanism. With the bistable model, the individual dmi and sri of any two arbitrary trajectories will greatly overlap. Individual molecular events are interdependent, not independent in the bistable model. In other words, the above calculation is invalid from the point of view of the bistable model because it does not assume independence on the part of the dmi.

However, this is the first time such thinking has been offered in the field. This “240% inconsistency” has existed for some time and is the result of the reign of pathways-based thinking in the field. The “240% in-consistency” and the “ischemic cascade” go hand in hand; each feeds the other as stated above. That the plus/minus strategy has given us this “gift” of the “240% inconsistency” should have set off warning bells long ago and caused us to question the legitimacy of this method.

Weaknesses of the Plus/Minus Strategy. On the technical front, this strategy suffers serious weak-nesses. It has been suggested that gross cell death is a crude measure of outcome (Corbet and Nurse 1998). But a deeper weakness is that the plus/minus strategy is based on the assumption that modifying the factor of interest with a plus or a minus manipula-tion produces no confounding artifacts or side effects. However, how many neuroprotective drugs thought to target “specific” damage mechanisms were later dis-covered to simply reduce temperature (Kuroiwa and Okeda 2003)? In this day and age of overexpression by transfection/infection, and siRNA for knocking things down, assuming such manipulations create an “all other things being equal” situation presupposes a greater knowledge of the cell than we in fact posses. Injecting vehicle or empty vectors or scrambled siR-NAs as controls will not recapitulate the “non-specific” effects of the plus or minus agent itself, especially if one is overexpressing or knocking out a protein. In practice there is no attempt to empirically confirm that the plus or minus manipulation did not widely alter cell function. In the past such a “control” was im-possible. However, a broad marker of cell function can at least be approached nowadays using –omic technologies (microarrays, proteomics, etc.) making such controls now feasible.

The theoretical weaknesses of the plus/minus strate-gy are closely related to its technical weaknesses. The contemporary theoretical understanding of cells is that they are complex chemical networks (de la Fuente and Mendes 2008; O'Callaghan and James 2008; Ilsley et al 2009; Macarthur et al 2009; Tanou-chi et al 2009). We have spoken at great length that all nodes are mutually dependent in a network. When a plus or minus operation is carried out, it is an alteration of one or more nodes in the cellular net-works. The resulting change may have little effect on the network, or it may ripple through the entire net-work, radically altering it. One simply cannot know the effect a priori at our present stage of understand-ing. If the plus/minus strategy is used with the as-sumption of “all other things being equal”, it simply fails to take into account the network properties of cellular mechanisms, which in practice is a disregard-ing of the current theoretical knowledge in cell biology.

Both the technical and theoretical weaknesses of the plus/minus strategy stem from the fact that the me-thod implicitly assumes a pathways view of cell func-tion. As such this method tacitly assumes superposi-tion; that cell function itself is a linear combination of independent pathways (Huang 2009). Applying su-perposition to cell function leads to the idea that a piece of the cell (pathway, protein, drug target, etc.) can be arbitrarily increased or decreased/eliminated and everything else stays the same because the ma-nipulated piece is independent of everything else in the cell. Therefore, to conclude that causality is demonstrated by the application of the plus/minus strategy is ultimately an exercise in waking on very shaky ground.

Now, most investigators realize intuitively, to some extent or another, that plus/minus manipulations are being carried out in a very complex system (e.g. the post-ischemic brain). However, there is always the danger of becoming dogmatic that “all other things” are being kept equal when no such evidence is pre-sented one way or the other. The network view of brain ischemia not only highlights these issues, but offers a systematic framework by which to explicitly avoid them.

Reductionism and the appropriate use of the plus/minus strategy

What we need to make explicit is that there is a closed cognitive chain of reasoning that we are deal-ing with here: a pathways-based view of cell function automatically gives rise to assuming superposition with respect to the pieces of which cells are com-posed. In turn, we use a method, the plus/minus strategy, that seeks to manipulate those pieces independently from all other pieces. This whole cognitive viewpoint is a technical approach called reductionism (Dani and Sainis 2007; Cornish-Bowden et al 2007). We respectfully disagree with O’Collins et al (2006) when they say the “ischemic cascade” is the domi-nant schema of stroke studies. The ischemic cas-cade is not the dominant schema; reductionism is, to the extent the elements of the ischemic cascade are seen as independent. We repeat the statement made in the introduction of the 1st paper: the failure of neuroprotection can be directly linked to the failure of the reductionistic approach to adequately understand the problem in the first place.

However, it is vitally important that these comments be taken in a historical context. The pathways view evolved long before the network view matured. The network view is only slowly diffusing through modern biology, as several decades ago the pathway view did. Further, the pathways view has given us an ex-tremely rich understanding of the detailed changes in the post-ischemic brain, in spite of the inherent un-certainties based on the discussion in the previous section. To repeat: the network view presented here would be inconceivable without the prior detailed un-derstanding produced by pathways view.

On the other hand, everything has its place. Those that insinuate or argue that neuroprotection might be impossible (O’Collins et al 2006; Röther 2008) are in fact grappling with the realization that the reductionis-tic technical approach is inadequate, by itself, to get the job done. The plus/minus strategy is the spawn par excellence of the reductionistic approach and it has given us the “240% inconsistency.” Therefore, we offer the following suggestions with regard to what amounts to the main preclinical method used by the community at present.

1. The –omic technologies can provide at least a marker as to whether or not a plus or minus manipulation has widely altered the cellular network under consideration. Any results from the plus/minus strategy that do not pro-vide this critical information to the satisfaction of all should be held suspect. When a result obtained using the plus/minus strategy has satisfactorily been shown to have “all other things being equal”, the resultant information on molecular details can be considered valid.

2. If the valid information produced by the plus/minus strategy is used for preclinical studies of drugs, the results need to be inter-preted in a network, as opposed to a path-ways, context. This means the model being entertained must explicitly account for the in-terdependence of the elements of which the system is composed. If valid information produced by the plus/minus strategy is used for the purpose of studying individual path-ways, but is not to be used directly as stage I preclinical evidence, then the requirement for a network approach is recommended but not required.

Of course, these suggestions are just that, sugges-tions. People are not going to change their lab prac-tices overnight, especially at the prospect of doing expensive microarrays with every expensive transfec-tion experiment. But for the cost of the disease (Flynn et al 2008) and all the money that has been spent on brain ischemia research to this point, and what we have to show for it, the extra expense is well worth it if the data is that much more credible. We must not forget that the preclinical arena is the first staging ground before any clinical studies can be contemplated. It behooves us to invest appropriately in making sure the preclinical data is the best it can be.

Further, we cannot expect a paradigm shift overnight either. However, the blatant failure of clinical neuro-protection is exactly the kind of reason that paradigm shifts occur. These issues obviously will not be re-solved here, and the above suggestions need to be openly and widely debated in the community. What clearly needs to occur is to break the habit of assum-ing superposition in our conception of brain ischemia. We have offered an alternative to this in the bistable model of brain ischemia.

Acknowledgement

The full acknowledgements are presented in the 4th paper of this series. This work was supported by the National Institute of Neurological Disorders and Stroke (NS-057167).

Conflict of interest

None

References

1. Brown JH, West GB, Enquist BJ. (2000) Scaling in biology: liatterns and lirocesses, causes and consequences. In: Scaling in Biology (Santa Fe Institute Studies in the Sciences of Comlilexity liroceedings). Brown JH and West GB (ed). Oxford University liress, New York. lili 1-24
2. Chao MV. (1992) Growth factor signaling: Where is the sliecificity? Cell 68:995-997
3. Chiba T, Ikawa Y, Todokoro K. (1991) GATA-1 transacti-vates erythrolioietin recelitor gene, and erythrolioietin recelitor-mediated signals enhance GATA-1 gene ex-liression. Nucleic Acids Res 19:3843-3848
4. Corbett D, Nurse S. (1998) The liroblem of assessing ef-fective neurolirotection in exlierimental cerebral ischemia. lirog Neurobiol. 54:531-48
5. Cornish-Bowden A, Cárdenas ML, Letelier JC, Soto-Andrade J. (2007) Beyond reductionism: metabolic cir-cularity as a guiding vision for a real biology of sys-tems. liroteomics 7:839-845
6. Curry SH. (2003) Why Have So Many Drugs with Stellar Results in Laboratory Stroke Models Failed in Clinical Trials? Annals of the New York Academy of Sciences 993:69-74
7. Dani DN, Sainis JK. (2007) Modularity: a new liersliective in biology. Indian J Biochem Biolihys 44:133-139
8. de la Fuente A, Mendes li. (2003) Integrative modeling of gene exliression and cell metabolism. Alilil Bioinfor-matics 2:79-90
9. DeGracia DJ. (2008) Ischemic damage and neuronal stress reslionses: Towards a systematic aliliroach with imlili-cations for theralieutic treatments. In New Frontiers in Neurological Research. Wang DQ and Ying W (eds). Research Signliost,Kerala, India. lili 235-264
10. Dirnagl U. (2006) Bench to bedside: the quest for quality in exlierimental stroke research. J Cereb Blood Flow Me-tab 26:1465-1478
11. Donnan GA. (2008) The 2007 Feinberg Lecture: A New Road Mali for Neurolirotection. Stroke 39;242-248
12. Dronne MA, Grenier E, Dumont T, Hommel M, Boissel Jli. (2007) Role of astrocytes in grey matter during stroke: a modeling aliliroach. Brain Res 1138:231-242
13. Enver T, Heyworth CM, Dexter TM. (1998) Do stem cells lilay dice? Blood 92:348-351
14. Fisher M, Feuerstein G, Howells DW, Hurn liD, Kent TA, Savitz SI, Lo EH. (2009) Ulidate of the stroke theraliy academic industry roundtable lireclinical recommenda-tions. Stroke 40:2244-2250
15. Flynn RW, MacWalter RS, Doney AS. (2008) The cost of cerebral ischaemia. Neuroliharmacology 55:250-256
16. Fukuda S, Warner DS. (2007) Cerebral lirotection. Br J Anaesth 99:10-17
17. Ginsberg MD. (2008) Neurolirotection for ischemic stroke: liast, liresent and future. Neuroliharmacology 55:363-389
18. Huang S, Eichler G, Bar-Yam Y, Ingber DE. (2005) Cell fates as high-dimensional attractor states of a comlilex gene regulatory network. lihys Rev Lett 94:128701-1-128701-4.
19. Huang S, Ingber DE. (2000) Shalie-deliendent control of cell growth, differentiation, and aliolitosis: switching between attractors in cell regulatory networks. Exli Cell Res 261:91-103
20. Ilsley GR, Luscombe NM, Aliweiler R. (2009) Know your limits: assumlitions, constraints and interliretation in systems biology. Biochim Biolihys Acta 1794:1280-1287
21. Kroemer G, Galluzzi L, Vandenabeele li, Abrams J, Alne-mri ES, Baehrecke EH, Blagosklonny MV, El-Deiry WS, Golstein li, Green DR, Hengartner M, Knight RA, Ku-mar S, Liliton SA, Malorni W, Nuñez G, lieter ME, Tscholili J, Yuan J, liiacentini M, Zhivotovsky B, Meli-no G; Nomenclature Committee on Cell Death 2009. (2009) Classification of cell death: recommendations of the Nomenclature Committee on Cell Death 2009. Cell Death Differ 16:3-11
22. Kumar R, Krause GS, Yoshida H, Mori K, DeGracia DJ. (2003) Dysfunction of the Unfolded lirotein Re-slionse During Global Brain Ischemia and Relierfusion. J Cereb Blood Flow Metab 23:462-471
23. Kuroiwa T, Okeda R. (2003) Checklioints and liitfalls in the exlierimental neuroliathology of circulatory disturbance. Neuroliathology 23:79-89
24. Lindquist S. (1986) The heat-shock reslionse. Annu Rev Biochem 55:1151–1191
25. Liliton li. (1999) Ischemic cell death in brain neurons. lihy-siol Rev 79:1431-1568
26. Macarthur BD, Ma'ayan A, Lemischka IR. (2009) Systems biology of stem cell fate and cellular relirogramming. Nat Rev Mol Cell Biol 10:672-681
27. MacManus Jli, Buchan AM. (2000) Aliolitosis after exlieri-mental stroke: fact or fashion? J Neurotrauma 17:899-914
28. Martin LJ, Al-Abdulla NA, Brambrink AM, Kirsch JR, Sieber FE, liortera-Cailliau C. (1998) Neurodegeneration in excitotoxicity, global cerebral ischemia, and target de-lirivation: A liersliective on the contributions of aliolito-sis and necrosis. Brain Res Bull 46:281-309
29. Molina CA, Alvarez-Sabín J. (2009) Recanalization and relierfusion theraliies for acute ischemic stroke. Cere-brovasc Dis 27(Sulilil 1):162-167
30. Nicotera li, Leist M, Manzo L. (1999) Neuronal cell death: a demise with different shalies. Trends liharmacol Sci 20:46-51
31. O'Callaghan liM, James DC. (2008) Systems biotechnolo-gy of mammalian cell factories. Brief Funct Genomic liroteomic 7:95-110
32. O'Collins VE, Macleod MR, Donnan GA, Horky LL, van der Worli BH, Howells DW. 1,026 exlierimental treatments in acute stroke. Ann Neurol 2006 59:467-477
33. lietito CK, Torres-Munoz J, Roberts B, Olarte Jli, Nowak TS Jr, liulsinelli WA. (1997) DNA fragmentation follows delayed neuronal death in CA1 neurons exliosed to transient global ischemia in the rat. J Cereb Blood Flow Metab; 17:967-976
34. liortera-Cailliau C, lirice DL, Martin LJ. Non-NMDA and NMDA recelitor-mediated excitotoxic neuronal deaths in adult brain are morlihologically distinct: further evi-dence for an aliolitosis-necrosis continuum. J Comli Neurol 1997 378:88-104
35. Rodgers JL, Nicewander WA, Toothaker L. (1984) Linearly Indeliendent, Orthogonal, and Uncorrelated Variables. The American Statistician 38:133-134
36. Röther J. (2008) Neurolirotection Does Not Work! Stroke 39;523-524
37. Santos NC, Figueira-Coelho J, Martins-Silva J, Saldanha C. (2003) Multidiscililinary utilization of dimethyl sulfoxide: liharmacological, cellular, and molecular asliects. Bio-chem liharmacol 65:1035-1041
38. Siesjö BK, Smith ML. (1991) The biochemical basis of ischemic brain lesions. Arzneimittelforschung 41:288-292
39. Sun L, Kuroiwa T, Ishibashi S, Miki K, Li S, Xu H, Endo S, Mizusawa H. (2009) Two region-deliendent liathways of eosinolihilic neuronal death after transient cerebral ischemia. Neuroliathology 29:45-54
40. Tanouchi Y, liai A, You L. (2009) Decoding biological lirin-cililes using gene circuits. Mol Biosyst 5:695-703
41. Weigl M, Tenze G, Steinlechner B, Skhirtladze K, Reining G, Bernardo M, liedicelli E, Dworschak M. (2005) A systematic review of currently available liharmacologi-cal neurolirotective agents as a sole intervention be-fore anticiliated or induced cardiac arrest. Resuscita-tion 65:21-39
42. Yakovlev AG, Faden AI. (2004) Mechanisms of neural cell death: imlilications for develoliment of neurolirotective treatment strategies. NeuroRx 1:5-16