Towards a dynamical network view of brain ischemia and reperfusion. Part II: a post-ischemic neuronal state space

*Corresponding Author:

Donald J. DeGracia, Ph.D.
Department of Physiology, Wayne State University, 4116 Scott Hall, 540 East Canfield Ave.
Detroit, MI 48201, U.S.A
Phone 313-577-6745
Fax 313-577-5494
E-mail: ddegraci@med.wayne.edu

Abstract

The general failure of neuroprotectants in clinical trials of ischemic stroke points to the possibility of a fundamen-tal blind spot in the current conception of ischemic brain injury, the “ischemic cascade”. This is the second in a series of four papers whose purpose is to work towards a revision of the concept of brain ischemia by applying network concepts to develop a bistable model of brain ischemia. We here build the bistable network model of brain ischemia. The central concept is that of a post-ischemic state space. Ischemia, as a quantitative pertur-bation, is envisioned to push the brain through a series of four phenotypes as a function of the amount of ischemia: the homeostatic, preconditioned, delayed neuronal death and necrotic phenotypes. The phenotypes are meta-stable attractors in the landscape of the post-ischemic state space. The sequence of the phenotypes derives from the mutual antagonism between damage mechanisms and stress responses, each conceived as aggregate ensemble variables. The competition between damage mechanisms and stress responses is posited to have the form of a bistability. Application of bistability to brain ischemia is grounded in the incontrovertible fact that post-ischemic neurons face the mutually exclusive decision to either live or die.

Keywords

Bistability; global cerebral ischemia; neuroprotection; preconditioning; post-ischemic state space

Abbreviations

3D      three dimensional

CBF      cerebral blood flow

CD      the attractor for cell death

CGI      complete global ischemia

D      delayed neuronal death region of post-ischemic state space

DM      effective total ischemia-induced dam-age

DND      delayed neuronal death

H      homeostatic region of post-ischemic state space

I      the amount of ischemia

IS      the amount of ischemia at the separatrix

N      necrotic region of post-ischemic state space

P      preconditioning region of post-ischemic state space

S      the attractor for the steady-state pheno-type of a neuron

SR      effective total ischemia-induced stress response capacity

TD      threshold of delayed neuronal death

TF      transcription factor

TN      threshold of necrosis

TP      threshold of preconditioning

3D      three dimensional

CBF      cerebral blood flow

Why “towards” a dynamical network view of brain ischemia and reperfusion?

We titled this series of papers “Towards…” for a good reason: we do not here present a formal network model of brain ischemia and reperfusion. A formal network model would consist of a set of equations, the answer to which is the state space. Instead, we discuss considerations that can move us toward con-structing such a formal network. We in fact work backwards, discussing what the state space of the post-ischemic brain should look like based on our empirical understanding of outcomes after brain ischemia. We then go under the hood of this hypo-thetical post-ischemic state space and show how it can be derived from a particular circuit motif, the bist-able motif. Bistability results whenever a system fac-es two mutually exclusive states (Chatterjee et al 2008). Post-ischemic cells indeed face a mutually exclusive decision: live or die.

The net result of our present effort is that we end up with a faux network model of brain ischemia. The model is faux because there are no network equa-tions behind it. However, as we shall see, a post-ischemic state space is in fact constructed from em-pirical considerations. We will discuss the additional hurdles required to convert this empirical state space to actual network equations. The present work is a necessary step towards discovering such equations by laying out the rationale and justifications for constructing the state space. The hope is that by airing these considerations in the literature, it will facilitate the discovery of the state space equations. So while the resulting model is “faux”, the discussions leading up to it are not, and we shall see (mainly in the 3rd paper) that the resulting post-ischemic state space proves surprisingly useful even at its present stage of development. We begin by providing an overview of the ideas and then filling in the details.

Overview

There are three steps we follow, the cumulative result of which is to effectively outline a bistable model of brain ischemia. Step one consists of describing the post-ischemic state space as a means to represent the phenotypes cells acquire after experiencing spe-cific amounts of ischemia. The second step is to ask how the state space landscape and associated phe-notypes are generated. This will be seen to be due to the inherent competition of the damage mechan-isms and the stress response, each considered as aggregate or ensemble variables. The third step is to show how a state space derived from the competition between the damage mechanisms and stress res-ponses is in fact an example of a bistable system. These three steps constitute the task of the present paper. However, additional development of the bist-able model of brain ischemia continues throughout the 3rd and 4th papers, elaborating on the basic framework presented below.

The post-ischemic state space represents ischemia-induced phenotypes

The essence of a network view of brain ischemia is to recognize that increasing amounts of ischemia will move the brain through distinct phenotypes. While ischemia is clearly a perturbation to the brain, we here think of this perturbation as analogous to, in some sense, a force. While we do not literally mean “force” in the technical physics sense, we need to metaphorically think of ischemia as “pushing” the configuration (or state vector) of a cell into other phe-notypes. The strength of this “push” is directly propor-tional to the amount of ischemia, I, as conceptualized along the lines presented in the 1st paper.

For reasons also discussed in the 1st paper we con-sider only complete global ischemia (CGI) and take its intensity (e.g. the amount of ischemia) to be syn-onymous with its duration. In this and the subse-quent two sections we build the post-ischemic state space, a landscape consisting of topological features (hills and valleys) that represent the possible pheno-types induced in cells by increasing amounts of ischemia, I.

Our point of departure is the following: Peter Lipton’s quote in the 1st paper talked about a threshold of ischemia, as does Wieloch’s sandwich model, but our present understanding of brain ischemia and reperfu-sion points to at least three important ischemic thre-sholds, three specific amounts of ischemia, which, upon passing, give rise to three distinct phenotypes in the post-ischemic brain.

The brain’s normal steady state (S). The first step in describing post-ischemic phenotypes is to define our baseline, which is the normal brain that has not expe-rienced ischemia. To this end, using cellular differen-tiation as our case study serves a dual purpose. Be-low in a subsequent section, it will provide a network model of bistability we can emulate and apply to ischemia. Here however it provides for us a model of the normal state of brain cells, which we can utilize as our baseline. Each terminally differentiated cell type in the brain got there by differentiation. That is, each cell type in the mature brain occupies its own stable attractor in the gene network state space of the organism. The attractor of each terminally diffe-rentiated cell type exists on a landscape containing all the cell types coded by that genome; these are the epigenetic landscapes first described by CH Wad-dington (1957). This attractor provides our baseline and we call this baseline the steady-state, S, of the terminally differentiated cell. S is that point in the organism’s gene network state space that corres-ponds to the configuration (i.e. pattern of gene ex-pression) of the terminally differentiated cell type.

An advantage of focusing only on CGI is that, unlike focal ischemia, the main target of global ischemia is the neuron (at least over a meaningful range of ischemic intensities). This allows us to narrow our focus specifically to neurons. However, the following logic would be expected to be applicable to the glia, vascular and immunological cells that are also altered following focal ischemia (discussed in the 4th paper). But for our present purposes, S is taken to be that point in the genetic state space of an organism that represents the attractor of terminally differentiated neurons. After presenting the state space, we dis-cuss the issue of neuron subtypes.

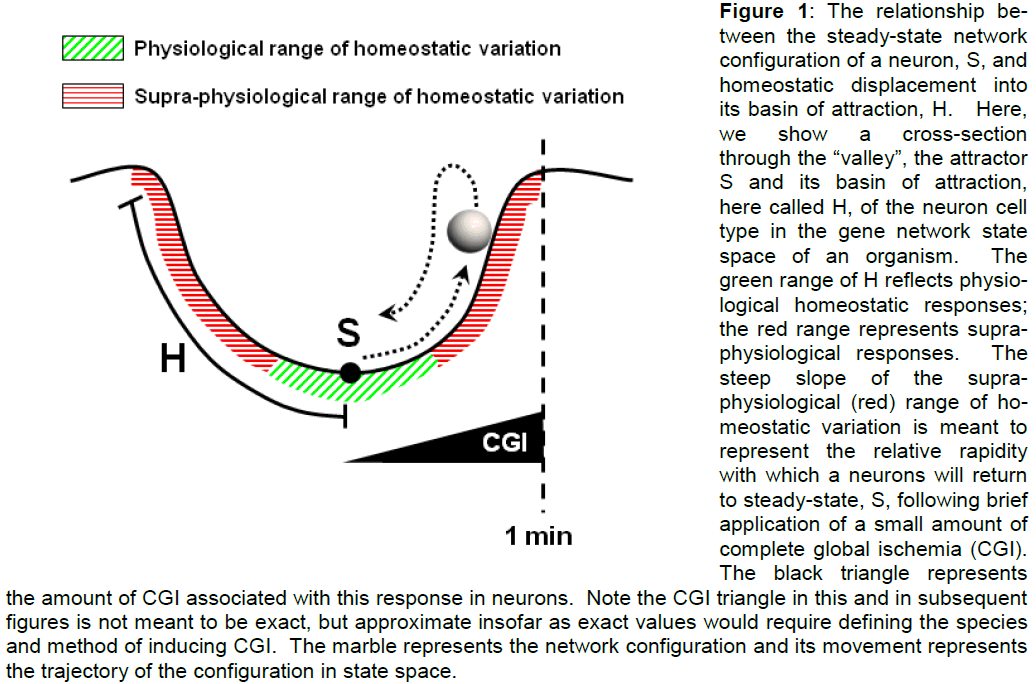
The homeostatic state (H). Now, while S is the low-est (e.g. most stable) point in the attractor of the neu-ron phenotype, there is still the rest of the valley. Technically, the valley surrounding an attractor point is called the basin of attraction. A basin of attraction is defined as the collection of points in the state space having the property that, if the system visits a basin point, it will inevitably settle back to the attrac-tor point (Huang 2009). For our purposes here, we consider the basin of attraction surrounding S to represent states that are homeostatic responses of the neuron to sub-pathological changes in blood flow. We thus term the basin of attraction around S the homeostatic state, H (Figure 1). Responses of neurons in H fall into two classes: (1) points close to S represent normal physiological responses (green re-gion, Figure 1), and (2) points farther away from S represent more extreme responses that are supraphysiological but could be considered sub-pathological (red region, Figure 1). We now explain the rationale of this distinction.

The first distinction arises because of the relationship between blood flow and neuronal function. It is well-known that neuron activity and local cerebral blood flow (CBF) are intimately related in the process of flow-metabolism coupling (Iadecola and Nedergaard 2007). Therefore, there is a nontrivial range of blood flows which underlie flow-metabolism coupling that will produce acute homeostatic changes in neurons. Such changes underlie normal neuron function in-cluding conduction, memory, etc. Neuronal res-ponses in the regime indicated by the green region of Figure 1 will include genetic changes underlying normal neuronal plasticity. Technically, what this implies is that the point S is not really a fixed point, but will alter as a function of neuronal plasticity and thus form a kind of probabilistic “cloud” (Huang, 2009). However, this is a subtlety not essential to our arguments and is mentioned only for the sake of completeness. For the purpose of building the post-ischemic state space, we may make the approxima-tion that S is a fixed point in the organisms’ genetic state space. Therefore, in terms of acute responses to changes in local CBF, we can take the points close to S to represent normal physiological responses of a neuron.

However, a neuron can experience homeostatic dis-ruptions that fall in a gray area between normal and pathological. Application of a small amount of CGI to a neuron falls in this gray area. We know that a very short duration of CGI (e.g. < 1 min) is not lethal to neurons. There will however be a momentarily displacement of neurons out of their normal energetic steady-state (Siesjö and Wieloch 1985). ATP levels will drop, but not to zero, nonetheless triggering cor-responding acute energy conservation processes in the neuron. These are very short-lived effects, last-ing only minutes after removal of a very brief CGI perturbation, after which time the neuron returns to its normal steady state, S.

In fact, the state we are describing here is what Kirino (2002) called “immediate preconditioning”. This form of preconditioning is more predominant in the heart, but it is also present in the brain. The essence of the supra-physiological range of the H state is the activa-tion of acute homeostatic responses that are outside the neuron’s normal response range, but that do not involve genetic reprogramming of the neuron into a stress response phenotype in response to the decrement in blood flow. Again, such supra-physiological responses occur when I < 1 min, but greater than the normal range of physiological local CBF variation.

With respect to the state space, this implies that there is some range around S in the basin that is relatively flat and contains the response of a neuron to normal homeostatic variation (again, flow-metabolism coupl-ing that would underlie normal neuronal plasticity). However, the second part of the basin where the su-pra-physiologic homeostatic disruption is represented is expected to have a steep slope. This slope would reflect the relatively intense neuronal responses to a disruption such as brief CGI, which in turn would in-duce a rapid return back to steady-state, S, after the disruption. In the case of immediate preconditioning, neurons reset to S within < 15 min after the brief CGI (Kirino, 2002). These ideas are illustrated in Figure 1.

A “time out” on what the state space represents. Fig-ure 1 is our first example of the marble moving on the post-ischemic state space landscape. We would like to clarify what this represents as it will be a recurring theme throughout the rest of the presentation. The moving marble is a visual device for depicting changes in the state vector of the neuron induced by the “force” of ischemia. In the 1st paper, we used examples where a point in the state space corres-ponded to a specific pattern of gene expression. However, in the post-ischemic state space each point represents the many responses of a neuron to the applied ischemia.

As stated in the 1st paper these responses fall into two classes: damage mechanisms and stress res-ponses. The reader may wonder how many damage mechanisms and many stress responses can be represented merely as a point. As explained in the 1st paper, state spaces are multi-dimensional. A point in the state space can have any arbitrary n components, each representing the state of one of the n nodes of the network. Thus, in the post-ischemic state space, each point represents all ischemia-induced damage mechanisms and stress responses, the entirety of which are taken to be the phenotype of the post-ischemic neuron. At this point, we simply introduce this key idea. We will continue to develop this notion into the 3rd paper and ask the reader’s patience as the concept is developed. At this point in the discussion, the key idea is that movement of the state vector (marble) through the state space represents changes in the phenotype of the neuron. On a certain level, this idea is not at all unfamiliar. Mendel (1866) worked in terms of pheno-types. The only difference between the classical Mendelian view and the network view is that the net-work view incorporates the idea of dynamic changes of phenotypes in real time and applies the concept to individual cells.

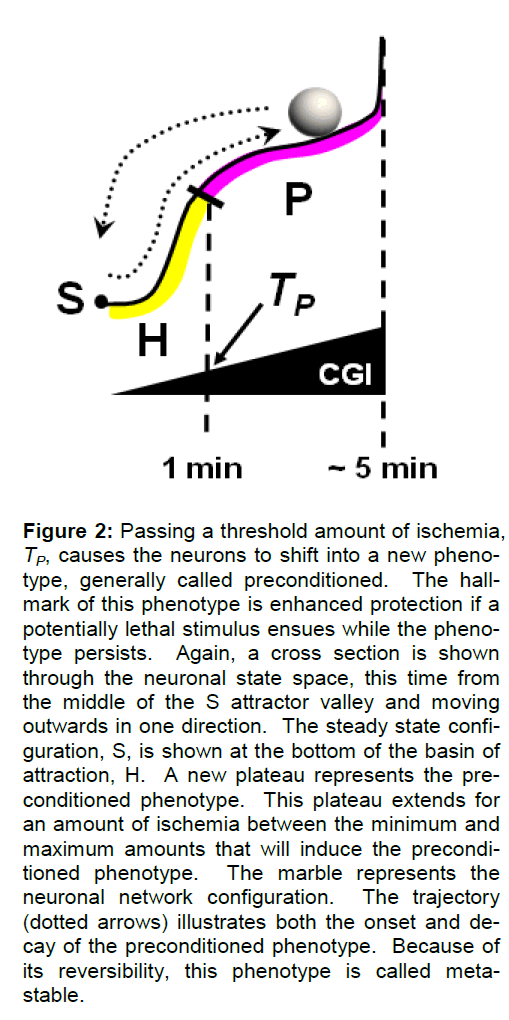
The preconditioned phenotype (P). A somewhat greater amount of CGI (~2-5 min) is still not lethal to neurons, but will push them over the first ischemic threshold, which we term the preconditioning thre-shold, TP. Theoretically, TP is a specific amount of ischemia, a specific value of I. Exposure to amounts of ischemia equal to or greater than TP puts neurons into a phenotype identifiably different from those in S or H. Neurons exposed to amounts of ischemia I > TP (but below a lethal threshold discussed below), can now withstand a subsequent lethal insult which neurons in S cannot withstand. This phenotype is what Kirino (2002) referred to as “delayed precondi-tioning” but we will refer to simply as preconditioning. While the field in general focuses on preconditioning as a form of neuroprotection, we here use the fact only as a marker that passing TP has put the neurons into a new phenotype. This phenotype lasts much longer than changes induced by H quantities of ischemia, but it is still completely reversible, persist-ing for several days before the neurons revert back to their normal steady-state, S (Kirino 2002). The pre-conditioned state consists not only of acute compen-satory changes as found in H, but also longer term changes in gene expression and protein synthesis that are responsible for its time course of expression (Kirino 2002). Thus, preconditioning is a form of temporary genetic reprogramming into a stress re-sponse phenotype. It is the genetic reprogramming into a stress response phenotype that distinguishes P phenotypes from H phenotypes, the latter of which do not so genetically reprogram.

From the point of view of the neuronal state space, we envision that the preconditioned phenotype P oc-cupies a plateau of responses that, on one hand are outside the normal basin of attraction (H) of the neu-rons, but on the other hand extend the basin of at-traction (Figure 2). The slope of this plateau is such that it does not form a permanently stable attractor valley, but instead has a very gently rising slope oriented such that the state vector will fall back to S. The slope in this case is intended to reflect the much slower kinetics of onset and shut-off of the precondi-tioned phenotype. However, since the plateau is sloped towards S, the neurons will eventually and inevitably fall back to S (illustrated by the trajectory of the marble in Figure 2). At some upper limit of CGI (a threshold we call TD, discussed in the next section), the neurons will no longer experience preconditioning as an outcome, setting the extent of this phenotype on the scale of CGI. In terms of state space, we en-vision the upper amount of ischemia to set a wall (a “quasi-potential” barrier) in the state space, an issue discussed further ahead. Thus, P is a meta-stable, reversible phenotypic alteration of the post-ischemic neuron. We are mute for the moment about the ge-nesis of this and the subsequent phenotypes, return-ing to that consideration after the post-ischemic neu-ronal state space has been described.

The delayed neuronal death phenotype (D). If we continue to increase the intensity of CGI past that required for preconditioning (e.g. to ~ 10 min), the second ischemic threshold is passed and this causes the delayed death of specific neuron populations, the selectively vulnerable neurons, yet spares resistant neurons (Kirino 2000). We therefore call this thre-shold amount of ischemia TD, the threshold of de-layed neuronal death (DND). Critically however, it is less the issue that the cell death is delayed than that the cell death occurs after the ischemic perturbation has been lifted. That is, the critical feature of passing TD is that the cell death will occur during reperfusion. Before discussing the associated state space, let us describe the final post-ischemic phenotype.

(A brief note on abbreviations: DND is delayed neu-ronal death and refers to the phenomenological death of neurons during reperfusion; D is the phenotype in the state space; TD is the threshold amount of ische-mia required to induce DND in a real brain or to move the configuration to the D phenotype in state space).

The necrotic phenotype (N). Finally, if the intensity of CGI is further increased (say to ~ 30 min), we pass a third ischemic threshold and move into a domain in which the ischemia is so intense that the neurons die acutely during the ischemia by necrosis (Siesjö and Smith 1991). The minimum amount of ischemia to trigger cell death during the ischemia itself is the ne-crotic threshold, TN, and the phenotype is N, the ne-crotic phenotype.

Brief summary of post-ischemic phenotypes. Before continuing, we briefly summarize. A very small amount of CGI will displace a neuron from S and cause it to enter the homeostatic state H, which is a very rapid and short lived response. Amounts of ischemia from TP to < TD will induce preconditioning in a neuron. Between TD and TN, some neurons, se-lectively vulnerable neurons, will die during reperfu-sion (i.e. after the ischemia) and therefore in a de-layed fashion with respect to the ischemic perturba-tion. Finally, if neurons experience amounts of ischemia > TN, they will die by necrosis during the ischemia.

Thereby we can see the critical role that the concept of the amount of ischemia, I, plays in the present thinking. It is the dependent variable of the model.

The post-ischemic state space and cell death

We now discuss adding cell death as a feature of the post-ischemic state space. To do so, we introduce two critical features into the post-ischemic state space.

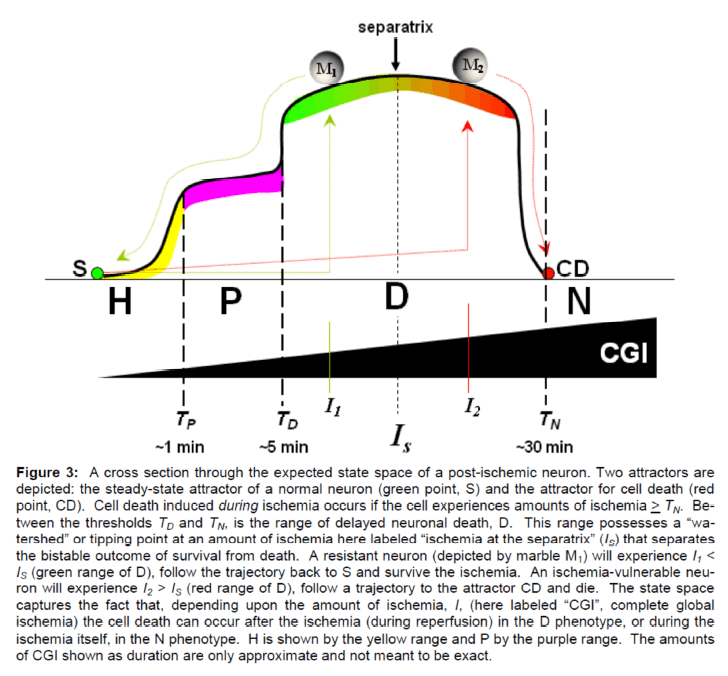
First, stated simply, cell death can be envisioned as an attractor in the state space. We do not here at-tempt a detailed justification as this has been pro-vided by others (Huang and Ingber 2000). However, by way of a brief justification, we note that apoptosis is a genetic program. As such, it is a specific pattern of gene expression and therefore occupies an attrac-tor in the genetic state space of an organism. Having said this, we want to strongly emphasize that this does not mean that we are saying post-ischemic neurons die by apoptosis, although many workers possess this viewpoint. In the present work we are completely agnostic about the mechanisms of cell death from the point of view of individual molecular pathways. However, that apoptosis is a genetic pro-gram is incontrovertible, and provides the most ob-vious and ready example of how cell death can be a phenotypic outcome of a genetic program and there-fore an attractor in an organism’s genetic state space. Thus, we can depict cell death in the post-ischemic state space by the addition of a second attractor to the state space (Figure 3). We will call this point in the state space the “cell death” (CD) attractor to be as general as possible, and to not insinuate a com-mitment to any specific molecular pathway of cell death.

The second feature we must introduce is a specific amount of ischemia that, for technical reasons to be explained ahead, we call I_S, the amount of ischemia at the separatrix. I_S is the “watershed” point on the state space curve. At I_S, the cell is at the tipping point between survival and death. As such it serves a function similar to Lipton’s and Wieloch’s concept of a cell death threshold (discussed in the 1st paper). However, for reasons to be elaborated as we pro-ceed, the concept of I_S is fundamentally a more systematic concept as it is a distinct property of the post-ischemic state space. I_S functions such that the sign of the slope of the state space curve reverses after I_S.

With addition of the attractor CD and the point I_S, we can now build the D and N phenotypes into the post-ischemic state space.

As a first approximation, we model the D phenotype to occupy a broad, gently sloped plateau, similar to P. Again the slope is used to reflect kinetic considera-tions, e.g. that cell death or recovery is delayed. The D plateau however, extends over a range of I that includes I_S. Thus, the slope of the state space in D will reverse at I_S. If the amount of ischemia is to the left of I_S, then the neuron will gradually fall back to S and survive the insult. This allows us to account for ischemia-resistant neurons. If the amount of ische-mia puts the neuron to the right of I_S, the cell will gradually but inevitably fall to the cell death attractor, CD. Thus we account for ischemia-vulnerable neu-rons.

Finally, if a neuron experiences an amount of ische-mia I > TN then the state space configuration moves during the ischemia on a trajectory from S directly to CD, and acute cell death results during the ischemia.

How to use the post-ischemic state space

The whole of our expected post-ischemic state space is summarized in Figure 3 which depicts a two di-mensional cross-section (e.g. a curve) through the state space landscape (the 3D state space is de-scribed later). The way the state space is intended to be understood and utilized is the following. The neu-ronal state vector is initially at S, the normal steady-state. Application of some specific amount of ische-mia, I, will displace the state vector to the point on the state space corresponding to that amount of ischemia. Two arbitrary amounts of ischemia are shown in Fig-ure 3. Applying an amount of ischemia I1 to the point S “pushes” the state vector from S to the point de-picted by marble M1. M1 is in the region of delayed neuronal death, D, to the left of I_S (e.g. I1 < I_S). After the state vector is so moved to that point on D, and the ischemia has ended, the state vector (marble) will then move (“roll”) leftward along the state space sur-face until it settles back to the point S. Hence M1 represents a neuron that survives the ischemia. M2 on the other hand is “pushed” by a greater amount of ischemia I2, to the right of I_S in region D (e.g. I2 > I_S). Thereafter, marble M2 will “roll” across the state space landscape to attractor CD and die. M2 there-fore represents the state vector of an ischemic-vulnerable neuron. The rate at which a state vector (marble) moves is reflected by the slope of the sur-face over which it moves.

One can readily see the obvious analogy between the post-ischemic state space and (frictionless) gravi-ty. Ischemia, as a “force”, imparts “energy” to the state vector (represented by the marble), “kicking” it uphill on the state space landscape. Then, analog-ous to releasing this energy, the state vector (marble) “rolls” back downhill to the lowest point, either S or CD. While this is a useful metaphor, it is technically inaccurate because the heights are quasi-potentials, not a real potential like gravity (Huang 2009). But the height is nonetheless a measure of the stability of the state vector and the analogy is accurate in that regard.

What this model physically represents is how ische-mia elicits responses, phenotypes, in the post-ischemic neuron. But these responses are unstable states for the neuron. To eliminate the instability in its phenotype, the neuron will either return back to its stable steady-state (S) or it will die (CD). The choice depends on the specific magnitude of ischemia, I, it has experienced.

The post-ischemic state space: issues and fea-tures

While the above first-pass at a post-ischemic state space offers many advantages (which are discussed in the 3rd paper), there are also obvious problematic issues we here briefly discuss. We consider: (1) neu-ronal subtypes, (2) the relationship between the P and D phenotypes, (3) cell death during either ische-mia or during reperfusion, and (4) the question of re-perfusion-induced damage.

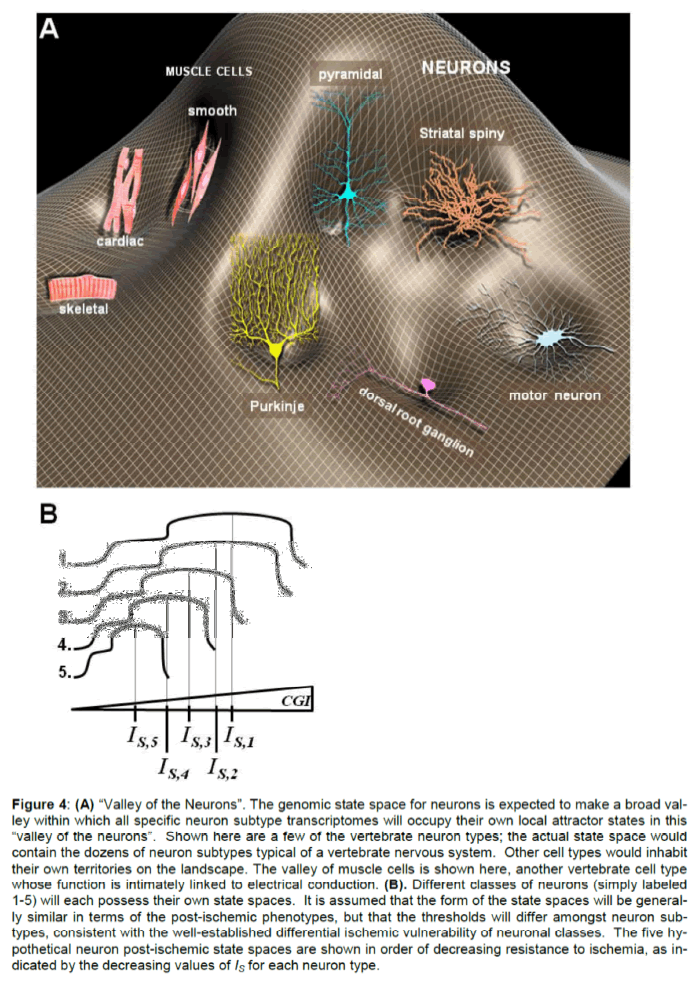
Neuronal Subtypes. We built the concept of the state space as if it belongs to that of a generic neuron. However, this is inaccurate and the issue requires clarification. One may think of a “Valley of the Neu-rons” in an organism’s genetic state space (Figure 4A). This valley will have within it many smaller local valleys, each being the attractor of a specific neuron type. We know different subtypes of neurons have different relative vulnerabilities to ischemia (Kirino 2000). For example, hippocampal CA1 neurons are most vulnerable to DND, and brainstem neurons re-quire considerably more ischemia to induce a compa-rable response. Therefore, the post-ischemic state space shown in Figure 3 should be thought of as a generic template for which the specific state spaces of individual neuron populations in individual organ-isms will need to be constructed. This is illustrated in Figure 4B showing a family of state spaces corres-ponding to different neurons in an organism after ex-posure to the same scale of CGI. Each neuron sub-type would be expected to display its own characte-ristic value of I_S.

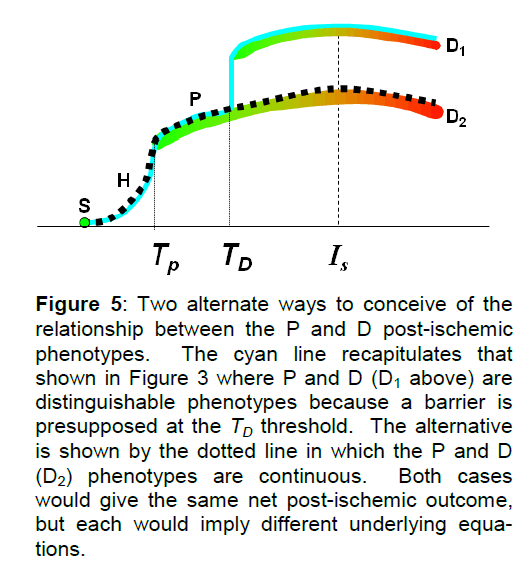
The relationship between P and D. Next we consider the distinction between the P and D ranges of pheno-types. The main reason we distinguish P and D as separate plateaus is that no cell death occurs on the P plateau (e.g. below the TD amount of ischemia), whereas cell death is imminent on the D plateau. This line of thinking raises important questions that have not generally been addressed. Preconditioning is generally not considered in relation to neurons that survive amounts of ischemia lethal to other neuron types (e.g. the selective vulnerability of CA1 after 10 min global ischemia vs. cerebral cortical or dentate granule cells that survive this insult). Our model makes conceivable the possibility that an ischemia-resistant neuron to the left of I_S in the D range (e.g. green range of D in Figure 3) is in fact in a precondi-tioned state. Such logic would apply, for example, to a dentate granule cell that will survive 10 min of glob-al ischemia in a rat. This would then mean there is not a wall or boundary between the P and D states and any phenotype in the range TP < I < I_S would be in some gradation of preconditioned states. The two possibilities are shown superimposed in Figure 5. This question is important because the form of the P-D boundary speaks to the form of the equations re-quired to generate the state space (discussed ahead).

If there is a P-D boundary, it may represent a proba-bilistic transition between recovery and cell death. The P range could be defined where the probability of cell death is strictly 0. In the D range when I > I_S, the probability of cell death could be defined as strictly 1.0. Then, the range TD < I < I_S, constituting the P-D boundary, may represent a range of increasing prob-ability of cell death following some probability function P(I).

While we are in no position to offer firm answers to these questions here, the utility of the bistable model is in raising these questions in the first place, ques-tions with clear empirical implications.

Cell death during either ischemia or during reperfu-sion. A critical feature of the state space is that it provides a natural classification of post-ischemic cell death. Cell death occurs either during ischemia or after the ischemia has been lifted. While this is well-known, the ideas presented here formalize this dis-tinction, providing a systematic means by which to classify ischemia-induced cell death, a topic explored in the 3rd paper of the series. In the terminology used here, the necrotic phenotype N means cell death dur-ing ischemia. The D phenotype refers to any death occurring after the ischemia has been lifted, or during reperfusion.

Reperfusion-induced damage. While the idea of “af-ter ischemia” is in practice the same as “during reper-fusion”, the distinction in the present context is impor-tant. In the scope of the above ideas it is the amount of ischemia, I, and not reperfusion that is the driving force of the system and the dependent variable of the model. It is well-established that additional damage mechanisms are initiated specifically in response to reperfusion (Safar 1986). However, we do not here distinguish between ischemia-induced and reperfu-sion-induced damage mechanisms. These are lumped together generically as “damage mechan-isms”.

While this may appear to be a limit of the current way of thinking, the justification for doing so is the follow-ing. Reperfusion-induced damage mechanisms are not independent of events initiated during ischemia. They are in fact a consequence of them. Consider for example lipid peroxidation, a reperfusion-specific phenomenon (Chan 1994). The degree of lipid pe-roxidation during reperfusion will be a function of the amount of suitable substrates produced during ischemia by lipolysis and delocalization of heavy metals (Traystman et al 1991; White et al 2000). Such substrates are not significantly present in a normal brain undergoing perfusion. Thus, it is not so much that reperfusion specifically induces its own forms of damage. It is more the case that certain forms of ischemic damage are latent during ischemia and only manifest during reperfusion due to the addi-tional substrates provided by the return of blood. Or in other words, damage during reperfusion is just an extended form of damage during ischemia. In fact, the same logic holds for stress responses as well. Most stress responses manifest during reperfusion, but in all cases the driving force is the net set of changes induced by ischemia. Therefore, given the causal links between ischemia-initiated events and subsequent events during reperfusion, we feel justi-fied to generically lump both forms of cell damage together. This consideration then leads us to the next major topic: the genesis of the phenotypes from the competition between damage mechanisms and stress responses.

Damage mechanisms and stress responses are driven by the amount of ischemia

Here we discuss the competition, the mutual anta-gonism, between the stress responses and the dam-age mechanisms. The shape of the post-ischemic state space landscape, that is, the series of pheno-types H, P, D and N will be seen to naturally follow from this competition. First we approach this competi-tion from an intuitive perspective and then briefly pro-vide a more systematic analysis. The present discus-sion sets the stage for us to consider bistability as the underlying circuit motif of the post-ischemic state space in the next section.

We note that we now begin to transition to a view in which the damage mechanisms and stress res-ponses are seen to be variables in their own right, variables that change as a function of I, the amount of ischemia. To this end, we define DM as the total effective damage produced by all damage mechan-ism in response to some amount of ischemia, I. We define SR as the total effective stress response capacity all of combined stress responses induced in a neuron by a given I. By defining DM and SR in terms of totals, we move towards viewing the aggregate or net effects of ischemia-induced damaging or protec-tive responses. In the 3rd paper we further formalize DM and SR. At this point we work with the qualitative definitions just provided.

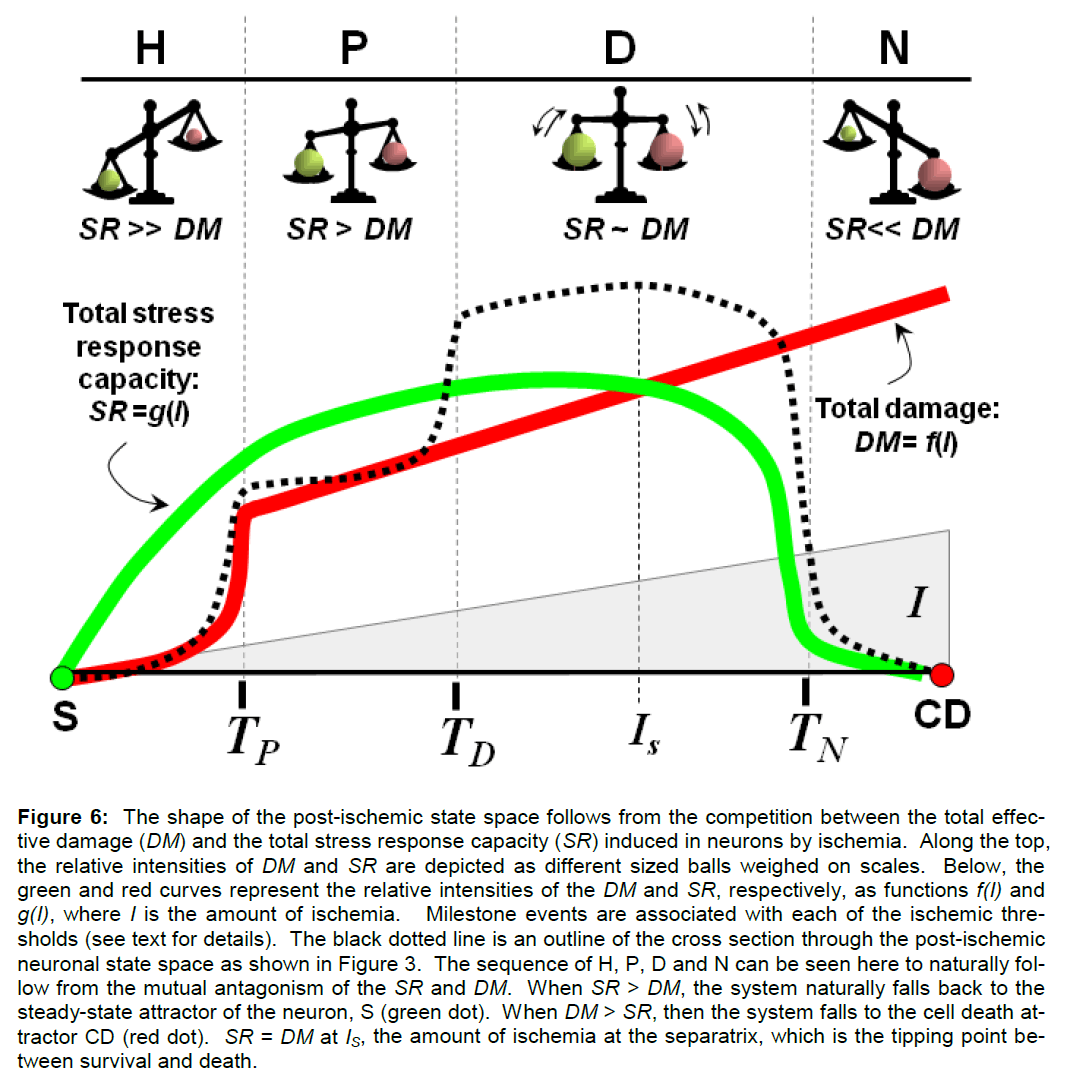
Intuitive considerations. Let us first contemplate the DM/SR competition intuitively. It is clear that the in-tensities of both DM and SR will be a function of the amount of ischemia, I. Both should increases as I increases. However, the increase is obviously not unbounded. When I > TN, cell death ensues, ending the competition in favor of total damage, DM. In con-trast, for a significant range in the state space, for all values of I < I_S, the stress responses, SR, win out over the total damage, DM, and the cell survives. These considerations lead us to hypothesize that the genesis of the thresholds reflects significant changes, milestone events, in the relative relationship between DM and SR. A likely scenario is as follows (see in conjunction with Figure 6). Note that we now also begin to speak of the state space ranges H, P, D and N as synonymous with specific ranges of amounts of ischemia.

In H, preexisting stress responses (e.g. not requiring transcription and translation) are rapidly activated, but I is low, therefore the total damage is relatively weak. That is, in H, SR >> DM. It seems most probable that what sets the TP threshold is the intracellu-lar concentration of ATP ([ATP]i). In the H range, [ATP]i does not reach zero. [ATP]i begins to ap-proach zero after CGI in a time frame consistent with preconditioning amounts of ischemia (e.g. ~ 2 min in the gerbil, Mrsulja et al 1986). After [ATP]i = 0, we expect a precipitous rise in total damage, DM, as well as a corresponding increase in total stress response capacity, SR, to cope. After TP, the increase in SR is reflected in the genetic reprogramming of neurons to the P phenotype. However, cell death never occurs during P which leads to the obvious conclusion that SR > DM through the entire range of P. It continues that SR > DM upon entering D, and the issue of whether the P-D boundary is a continuum or makes a discreet break at TD was discussed above (Figure 5).

Upon entering D, we encounter two new factors. The first involves saturation of the stress responses. As I increases through D, the total damage, DM, will con-tinue to increase. However, we expect that total stress response capacity, SR, will begin to level off. We expect SR to level off because of saturation. This is a key point. Stress responses are, in general, enzyme-mediated. As with any enzyme system, stress responses are subject to saturation. At some value of I, the amount of damage produced will defini-tively exceed the capacity of the induced stress res-ponses to process the damage, hence saturation. On the other hand, many of the DM are not enzyme-mediated but are non-physiological chemical reac-tions induced by toxic products formed during ische-mia. As such, they are limited only by substrate availability (e.g. lipid peroxidation, for example, is not enzyme-mediated, and will continue as long as sub-strates are available). Thus, we do not expect satu-ration to be a general property of DM.

Second, recall that SR and DM are mutually inhibito-ry. Since DM increases across the D range, but SR saturates, this would set up a situation where the in-hibition of SR by DM has a greater and greater effect. That is, we expect an acceleration of the inhibition of SR by DM through D. This will cause a decrease in the maximum (saturated) amount of SR and cause the dip in SR shown at the top end of the D range (green curve, Figure 6).

In short, once TD is passed, SR will initially level off due to saturation, and then decrease because of the accelerated inhibition by DM. At some point in D therefore, DM will become greater than SR. The amount of ischemia, I, after which DM > SR is to the right of I_S. Or said slightly differently, I_S is that amount of ischemia where SR = DM (Figure 6, dashed black line at I_S). Defining I_S as the amount of ischemia at which SR = DM in fact provides a formal rationalization of why I_S is the tipping point between cell survival or cell death.

Finally, when I > TN, the SR are completely over-whelmed, the DM completely dominate, and the cell dies acutely during the ischemia, giving rise to the N phenotype.

Figure 6 illustrates the above points in two ways. First, changes in DM and SR are depicted by scales measuring their relative intensities, metaphorically depicted as weight. Second, changes of DM and SR are displayed in a more precise fashion as hypotheti-cal curves that change as a function of the amount of ischemia, I. The curves can be designated as func-tions f and g such that DM = f(I), and SR = g(I). The curves f and g in Figure 6 are hypothetical, but none-theless educated guesses of the relative intensities of DM and SR as functions of I, based on the considera-tions discussed above. While hypothetical, these curves in fact are quite important. In principle, the post-ischemic state space can be derived using the equations that would generate the curves f and g as input functions. If real empirical curves of f and g can be measured, a formal network model will be possi-ble. We return to this key issue ahead when discuss-ing mapping the curves f and g to a bistable state space.

Kinetics verses thermodynamics. The above is intui-tive and informative as it goes, but there is a more systematic way to approach the issue of the relative intensities of SR and DM as a function of I. This in-volves the general viewpoint that any chemical reac-tion can be controlled either by kinetic or thermody-namic factors (Sykes 1986). Kinetic factors predomi-nate if the rate of a reaction is very fast: fast reactions occur when the energy of activation is low. If time allows, the most stable reaction products will form, allowing thermodynamic equilibrium to dominate the system. The most stable reaction products are those with the lowest energy (or highest entropy), although getting to them may require passing a higher energy of activation. The reader will recall that the fastest reaction product is not always the most thermody-namically stable. Both kinetic and thermodynamic forms of control factor importantly in the sequence H, P, D and N. Kinetic control dominates the beginning and end of the sequence, and thermodynamic control dominates the middle of the sequence.

Events in both H and N occur because very fast reac-tion kinetics are involved. In H, rapid execution of pre-existing homeostatic mechanisms allows the cell to quickly re-enter S upon lifting the slight ischemic perturbation (e.g. Figure 1). In N, the cell proceeds to the attractor CD because, at high amounts of ischemia, the rate of damage massively overwhelms the rate at which the cell can cope, e.g. the rate of stress response onset. Thus, in H and N, the relative intensities of the DM and SR are set by kinetic factors.

In P and D, however, events happen over relatively much longer time periods. P takes time both to onset and to decay. This is clearly due to the requisite changes in transcription and translation leading to the P phenotype, and the eventual decay back to the S phenotype. Similarly in D, it takes time for the cell death to occur; hence we call it “delayed”. Whatever the specific constellation of events underlying DND, we can infer, on the basis of the relative time frame involved, that these involve some type of steady-state equilibrium between DM and SR. It cannot be a true thermodynamic equilibrium because the system un-der consideration, the ischemic brain, is not a closed system; hence a steady-state is expected to evolve between SR and DM. When SR > DM (e.g. to the left of I_S), then the products of the stress responses do-minate the products of the damage mechanisms by some type of steady-state process. The opposite is true on the other side of I_S: damage products will dominate over those of the stress responses via some type of steady-state process. Thus, thermo-dynamic, not kinetic, factors determine the relative intensities of the DM and SR in the P and D domains.

In fact, we can say that, within the scope of our think-ing, the kinetic-based death in N and the thermody-namic-based death in D are precisely the causes of cell death during ischemia or during reperfusion, re-spectively. We here only introduce the notion that our model provides an alternative view of cell death causality, and return to this critical point in the 3rd pa-per of this series.

Summary. To summarize, we have in this section explained how the sequence of phenotypes in the post-ischemic state space, H, P, D and N, follow di-rectly from the mutual antagonism between SR and DM. With network thinking, we can understand the evolution of the phenotypes and make logical and systematic statements about ischemia-induced cell death. In fact we can state in precise terms the causes of ischemia-induced cell death.

This all follows with no reference whatsoever to the underlying details, a perhaps surprising situation to advocates of the traditional view that the causes of cell death are to be found somewhere in the fine de-tails of the “ischemic cascade”. On the other hand, the view presented here would be impossible to con-ceive without the detailed understanding of ischemia-induced damage and stress responses accumulated over the past few decades. As previously stated, the network view unifies and envelopes (encompasses) our present understanding of brain ischemia. It is a generalization and abstraction of decades of detailed results.

The final topic now to consider is how the DM/SR competition may be modeled with a bistable circuit to produce the post-ischemic state space.

Bistability and the post-ischemic state space

To do this section justice, we must briefly discuss bistability and review additional details of how the differentiation examples discussed in the 1st paper were modeled as bistable systems.

Bistability. Bistability is a common form of biological regulation and occurs whenever a system faces two mutually exclusive outcomes (Craciun et al 2006; Chatterjee et al 2008; Pomerening 2008). Examples of biological systems exhibiting bistable behavior in-clude sonic hedgehog signal transduction (Lai et al 2004), determination of cell fate (discussed ahead; Huang et al 2007), microbial sporulation (Igoshin et al 2006), growth factor-induced endocytosis (Zwang and Yarden 2009), cell cycling in xenopus oocytes (Ingolia 2005), the alternation between REM and NREM sleep (Karlsson et al 2004), and apoptosis (Wee and Aguda 2006), among many others.

It is surprising that in these and other complex multi-dimensional systems, the control of outcome can be reduced to two mutually antagonistic variables. We continue with the example of differentiation started earlier to illustrate how in practice one models a sys-tem as bistable. In doing so, the logic of reducing the complex changes induced by brain ischemia to only two mutually antagonistic variables, DM and SR, will be seen to be a maneuver that allows us to frame brain ischemia as another example of bistability in nature.

GATA1/PU.1 Control of FDCP Cell Differentiation. We briefly review the work of Huang et al (2007) on the differentiation of FDCP-mix (FDCP) progenitor cells into either erythroid cells or myeloid/monocytic cells. This is a bistable system in which the differen-tiation of FDCP cells into either erythroid or myelo-id/monocytic cells is a mutually exclusive decision.

The mutual exclusivity of the decision rests on elicit-ing different patterns of gene expression in the FDCP precursors. As is now well known, lineage specifica-tion is often controlled by “master” transcription fac-tors (TFs) (Kim et al 2009). These are TFs that sit at the top of a hierarchy of gene control. Activation of the master TF induces downstream TFs that may induce further downstream TFs, where the final set of downstream TFs turns on the genes of the final diffe-rentiated phenotype (Boheler 2009).

The lineage fate decision of the FDCP cells is con-trolled by the mutual antagonism of two master TFs. GATA1 triggers erythroid differentiation and PU.1 triggers monocytic differentiation (Huang et al 2007). Overexpression of either TF by transfection will in-duce its respective phenotype (Graf 2002). Key to this whole system, GATA1 and PU.1 are mutually inhibitory. GATA1 suppresses PU.1 transcription, and vice versa (Huang et al 2007). Therefore, the entire complex set of hierarchical changes in the gene regulatory network of the FDCP cell can be re-duced simply to the mutual antagonism between GATA1 and PU.1, allowing FDCP differentiation to be modeled as a bistable system.

We point out that when we discussed gene network state spaces in the 1st paper these were described in terms of Boolean networks, and the input functions were binary. The following model of GATA1/PU.1 bistability is not binary but is modeled using conti-nuous input functions where protein concentrations are continuous, not binary, variables (Alon 2006). Ahead, we emulate this approach and model the DM/SR competition also in terms of expressing these as continuous, not binary, variables.

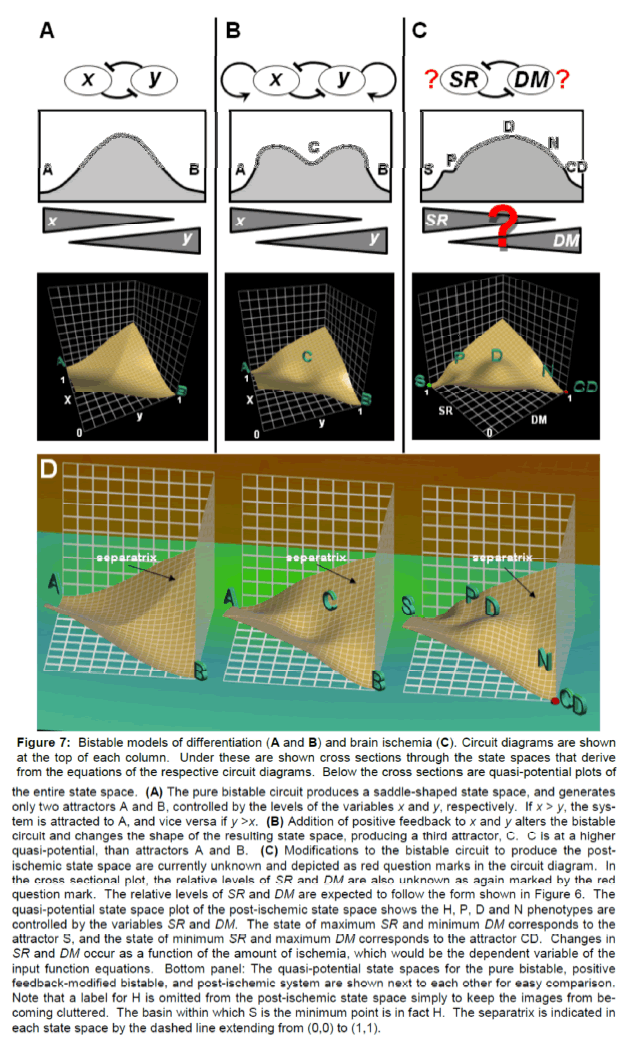
Modeling the GATA1/PU.1 Competition as a Bistable System. Figure 7 illustrates the bistable models of the GATA1/PU.1 competition (Figure 7A and B) and of brain ischemia (Figure 7C). Images shown in Fig-ures 7A and 7B are precise adaptations of data from Huang et al (2007). Here, the concentrations of GATA1 and PU.1 are notated as x and y. Notating Figures 7A and 7B generically is meant to illustrate that the underlying equations are generic, and not dependent upon the specifics of the GATA1/PU.1 system. The underlying generic model is that of a bistable system. The GATA1/PU.1 system happens to fit this pattern. We argue in the next section that brain ischemia also fits this pattern. The circuit re-presentations for each system are shown across the tops of the columns in Figure 7.

Figure 7A shows a pure bistable network that models only the mutual antagonism of x and y. Under the circuit diagram is a cross section through the result-ing state space. The points A and B are the attrac-tors associated with high [x] and high [y], respectively. If A is the erythroid phenotype, then x represents GATA1. Similarly, if B is the monocytic phenotype, then y represents PU.1. One can see that if [x] > [y] (e.g. [GATA1] > [PU.1]), then the system is attracted to A, the erythroid phenotype, and vice versa if [y] > [x]. At the center of the cross section where [x] = [y] is again a “watershed” point where the slope reverses sign. On either side of this “watershed” point, the sys-tem is fated to move to its respective attractor. Simp-ly stated, in this pure bistable circuit, the TF with the higher concentration wins the competition and deter-mines the outcome phenotype.

Underneath the cross section is a quasi-potential plot of the entire state space. In 3D, the state space in Figure 7A resembles a saddle (but it must be kept in mind that the state space itself is a two dimensional surface in x and y and the 3rd dimension is a quasi-potential projection). The state space bends down to the attractors at A and B, the lowest (e.g. most stable) points in the state space. The x and y axes extend from 0 to 1, but the range is arbitrary and can simply be thought of as a normalized range. Note that A is the point (1, 0), the maximum of x and the minimum of y, and vice versa for attractor B. All other points on the state space represent different proportions of x and y and correspond to all possible combinations of concentrations of the two TFs. All other points on the surface are unstable relative to the attractors (e.g. are at some higher point in the quasi-potential 3rd dimension). The highest, most unstable points of the state space are at (0, 0) and (1, 1). The “watershed” point in the cross section is actually a point on the line (technically, geodesic, because the 2D surface is bent) from (0, 0) to (1, 1). This line is called a sepa-ratrix; it is the unstable state between the two attrac-tors in which the system is poised to go in either di-rection. The separatrix is designated on each state space in Figure 7D. We can now see why the term “ischemia on the separatrix”, I_S, was introduced earli-er. It refers to the point on the state space cross-section that lies on the separatrix of the 3D state space.

One of the objectives of Huang et al (2007) was to generate a state space that contained not only the final differentiated phenotypes (e.g. A and B), but also included the attractor for the undifferentiated FDCP cells. To do this, he modified the input func-tions as shown in Figure 7B. He added one addition-al feature about GATA1 and PU.1 to the bistable cir-cuit: each activates its own transcription. This is now depicted in the circuit diagram by the rounded arrows emanating from and returning to x and y in Figure 7B. This modification adds positive feedback to each TF’s control of its own transcription.

Adding positive feedback to the circuit modified the parameters of the input function equations (Huang et al 2007). The effect on the resulting state space is shown again in cross section and as a quasi-potential plot (Figure 7B). By adding the self-activation of each TF, the input functions now generated a third attractor in the state space, here labeled C. The new attractor C represents the FDCP progenitor cell. It should be noted that the new attractor C fell along the separatrix of the pure bistable model, and generated a tristable system. However, attractor C is at a high-er quasi-potential than either A or B, thereby making it inherently less stable than A or B. In this fashion, Huang et al (2007) were successful in generating a realistic model of the phenotypes of the FDCP cell by simply adding only one biologically relevant fact to the pure GATA1/PU.1 bistable circuit: each TF acti-vates its own transcription.

Bistability and Brain Ischemia. The above was ne-cessary to set the background to discuss how the post-ischemic state space derives from a bistable competition between DM and SR. The important take-home message is this: one can modify the input functions of the pure bistable circuit and alter the shape of the state space. Such modifications in-volve adding reasonable additional features to the core bistable antagonism of the two variables. We now discuss possible ways to modify the pure bista-ble circuit to get equations that give us back the post-ischemic state space as shown in Figures 3 and 7C.

The post-ischemic state space is now depicted to mimic as closely as possible the results of Huang et al (2007) (Figure 7C). The images shown in Figure 7C constitute precisely the faux bistable network model of global brain ischemia. We can envision the end result. The issue is how to work backwards from the surface in Figure 7C to the input functions.

Mapping Ischemia and Differentiation. Let us first discuss the leaps in logic required to map the ische-mia problem to the differentiation problem. This mapping occurs through a series of substitutions:

1. Where FDCP differentiation is control by two mutually antagonistic transcription factors, brain ischemia is controlled by two mutually antagonistic abstract variables, DM and SR.

This may seem an unequal substitution in that GATA1 and PU.1 are physical, individual proteins, whereas DM and SR refer to total effects of many individual damage and stress responses, respectively, induced in neurons by ischemia. The issue here in-volves identifying two mutually antagonistic factors that control the system of interest. It happens to be physical proteins in the GATA1/PU.1 system. For brain ischemia, it happens to be the consequence associated with any specific ischemia-induced change. One is hard pressed not to assign a value of “good” or “bad” to any particular change identified in the post-ischemic brain. Or we could as well say “contributes to survival” and “contributes to death”. If there is some other possible consequence of an ischemia-induced change, it escapes this author. If a change is “neutral” (with respect to outcome) then why consider it? There is the possibility that a specif-ic change can flip state as a function of its position on the state space landscape. That is, a particular re-sponse could go from “good” (SR) to “bad” (DM) or vice versa. In such a fashion we could formally mod-el Eng Lo’s (2008) suggestion about the “biphasic” nature of stress responses. Here we simply point this out but do not discuss it further.

Therefore, we now see the main reason for classify-ing all changes induced in the brain as either contri-buting to survival (stress responses) or to cell death (damage mechanisms) and further, lumping these together in aggregate as the variables DM or SR. Doing so provides two mutually antagonistic variables that allow us to model brain ischemia as a bistable system. In the 3rd paper we address the relationship between the variables DM and SR and the many in-dividual molecular changes of which each consists. At this point in the discussion, we justify this leap in logic by the simple fact that it seems to work.

2. Where the plots in Figure 7A/B are plots of protein concentrations (x and y), we substi-tute the intensities of the DM and SR.

This does not seem unreasonable as concentrations are nonnegative continuous variables, and as Figure 6 indicates, the intensities of the DM and SR can so be depicted as well.

3. Where the changes in concentrations of x and y are a function of time in the input func-

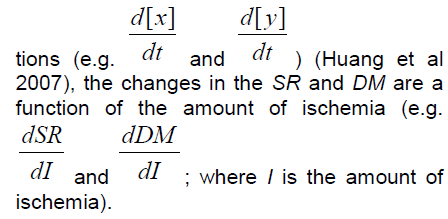
Even though we discussed the relationship between the amount of ischemia, I, and duration in the 1st pa-per, the explicit role of time in the change of the in-tensities of the SR and DM, considered as conti-nuous variables, is obviously complicated. The dis-cussion of kinetic and thermodynamic control would factor in here. It is likely that being able to formulate this question precisely in terms of rate and steady-state equilibrium expressions will allow derivation of the proper input functions for the post-ischemic state space. These would be precisely the functions f and g discussed earlier.

4. Where A and B are differentiated phenotypes, for brain ischemia these correspond to the normal neuron phenotype S and the cell death phenotype CD. No caveats can be envisioned as to why substituting phenotypes would present a problem.

Comparison of the Post-Ischemic and Differentiation State Spaces. Let us next compare the bistable re-presentation of the post-ischemic state space to those of differentiation. In Figure 7C, the cross sec-tion through the state space from point S to point CD captures all the features shown previously in Figure 3. Under the cross section, the intensities of the DM and SR are depicted as concentration (intensity) triangles by analogy to the Huang et al (2007) data. These however are inaccurate as depicted, thus the red question mark through them. The main inaccuracy is that they are shown as symmetric. From Figure 6, it is clear that they should be asymmetric because, as discussed, the SR and DM do not both increase in the same manner as a function of the amount of ischemia, I. At present, the best that could be ac-complished is to estimate input functions from the curves of DM and SR as shown in Figure 6; a chore for a future paper.

The 3D post-ischemic state space representation has several features different from those of the differen-tiation state spaces (easily compared in panel D of Figure 7, where all three are aligned next to each other). First, the post-ischemic state space is clearly asymmetrical across the separatrix, whereas both differentiation state spaces are mirror images across the separatrix. The symmetry in the differentiation cases is due to symmetric parameters in the input functions (Huang et al 2007). Choice of asymmetric parameters would generate an asymmetric space, but these would simply be distorted mirror images across the separatrix. The asymmetry in the post-ischemic state space is of a more fundamental nature, being due to the P phenomena on the S but not the CD side of the separatrix. P simply does not mirror image itself functionally. Thus, we see the issue of the P-D boundary is nontrivial and reflects the intrin-sic asymmetry of the post-ischemic state space.

The circuit diagram for the post-ischemic state space is shown with question marks because we do not yet know exactly how to modify the pure bistable circuit to generate the post-ischemic state space. For the GATA1/PU.1 bistable circuit, adding positive feed-back altered the state space in Figure 7A by generat-ing a shallow valley, the attractor C, in Figure 7B. We require the opposite change in the post-ischemic state space: a low flat hill to represent the D pheno-type. In addition the slopes associated with the H and N subregions of the state space are not expected to be mirror images.

Just to go through the intellectual exercise, if we, by analogy to the differentiation case in Figure 7B, add positive feedback to DM and SR, that would mean that damage would beget damage and the stress responses would induce themselves. Neither of these is physically realistic. Generally, stress re-sponse pathways are the opposite, they are self limit-ing. As stress gene products accumulate, they inhibit their own transcription, as for example with the heat shock response (Balakrishnan and De Maio 2006). In addition, as we said, SR is expected to saturate with increasing I. And while some damage mechanisms are chain reactions (again, lipid peroxidation), in gen-eral damage does not increase in a positive feedback after ischemia has ended. No, it seems reasonable, as a first approximation, to assume that DM increas-es as a linear function of I (after TP), as depicted in Figure 6. So, while we know positive feedback is not the required modification to the pure bistable circuit, going through this exercise illustrates the type of thinking required to find the necessary modification(s).

As the above discussion illustrates, the bottle neck to getting input functions lies precisely in answering the question: how is the pure bistable circuit to be mod-ified to alter the shape of the state space to match that of our post-ischemic state space that we have derived based on the mass of empirical evidence? A first stab at an answer is that addition of saturation to the function SR = g(I), and leaving the function DM = f(I) linear with respect to I (e.g. when I > TP) may generate the shape we have here hypothesized for the post-ischemic state space. There are also re-lated empirical questions:

1. What are the real graphs (or some reasona-ble approximation) of the relative intensities of the SR and DM as a function of the amount of ischemia, I? What molecular markers could provide this information?

2. Is the P-D boundary (e.g. at TD) a continuum or is there a wall (quasi-potential barrier) there (Figure 5)? Again we raise this point because P introduces an intrinsic asymmetry to the state space. This is not a question to be answered by theory. It needs to be ans-wered empirically by a demonstration (or not) that resistant neurons in D are in fact pre-conditioned. To our knowledge, this issue has not been considered before, but the is-sue is clearly experimentally accessible, and answering it will provide an important clue to the shape of the post-ischemic state space.

Open ends

On one hand it is perhaps unsatisfying that this story does not yet have a closed ending, and that we in-stead end this discussion with our sleeves rolled up considering technical issues. This is science after all, it is what we do, and many hands make light work.

On the other hand, we have here the beginnings of a viable reformulation of what brain ischemia is. The core of this reformulation is to model brain ischemia as a bistable system in a network context. Again, and quite obviously, post-ischemic neurons face the mutually exclusive decision to either live or die. Re-cognizing that bistability underlies brain ischemia brings it into the distinguished company of a myriad other biological processes that have bistability at the core of their operation.

Clearly the approach described here is not simply a metaphor or vague insight. It provides a new means to conceptualize, systematize and mathematically model brain ischemia. It is an alternative to the “ischemic cascade” as an explanatory framework. It does not reject the “ischemic cascade”; it encom-passes it in a new context where the myriad details of the “ischemic cascade” become subsumed as the points of the state space (more said on this in the 3rd paper).

This “Brain Ischemia 2.0” offers new insights into the causes of cell death by introducing the kinetic and thermodynamic explanations completely independent of any specific physiologic or molecular detail. It can unify our conception of brain ischemia by bringing all the ischemia-induced phenomena within the scope of one mathematical framework. Finally, the model hints at a general theory of cell injury. The logic used here could be applied to other brain injuries (and in fact has, Villoslada et al 2009), other cell types, other organs. While the sky is the limit in this regard, as the above makes plain, we still have to complete the project of modeling brain ischemia before moving on to other applications. But even at its present stage of development, the Brain Ischemia 2.0 viewpoint offers a fresh look at the current crisis in therapeutics, which we discuss in the next, the 3rd paper of this series.

Acknowledgement

The full acknowledgements are presented in the 4th paper of this series. This work was supported by the National Institute of Neurological Disorders and Stroke (NS-057167).

Conflict of interest

None

References

1. Alon U. (2006) An Introduction to Systems Biology: Design lirincililes of Biological Circuits. Chaliman &amli; Hall/Crc . London, UK
2. Balakrishnan K, De Maio A. (2006) Heat shock lirotein 70 binds its own messenger ribonucleic acid as liart of a gene exliression self-limiting mechanism. Cell Stress Chalierones 11:44-50
3. Boheler KR. (2009) Stem cell liluriliotency: a cellular trait that deliends on transcrilition factors, chromatin state and a checklioint deficient cell cycle. J Cell lihysiol 221:10-17
4. Chan liH. (1994) Oxygen radicals in focal cerebral ische-mia. Brain liathol 4:59-65
5. Chatterjee A, Kaznessis YN Hu W-S. (2008) Tweaking biological switches through a better understanding of bistability behavior. Current Oliinion in Biotechnology 19:475–481
6. Craciun G, Tang Y, Feinberg M. (2006) Understanding bistability in comlilex enzyme-driven reaction networks. liroc Natl Acad Sci USA 103:8697-8702
7. Graf T. (2002) Differentiation lilasticity of hematolioietic cells. Blood 99:3089–3101
8. Huang S, Guo Yli, May G, Enver T. (2007) Bifurcation dynamics in lineage-commitment in biliotent lirogenitor cells. Dev Biol 305:695-713
9. Huang S, Ingber DE. (2000) Shalie-deliendent control of cell growth, differentiation, and aliolitosis: switching between attractors in cell regulatory networks. Exli Cell Res 261:91-103
10. Huang S. (2009) Relirogramming cell fates: reconciling rarity with robustness. BioEssays 31:546–560
11. Iadecola C, Nedergaard M. (2007) Glial regulation of the cerebral microvasculature. Nat Neurosci 10:1369-1376
12. Igoshin OA, lirice CW, Savageau MA. (2006) Signaling network with a bistable hysteretic switch controls deve-lolimental activation of the sigma transcrilition factor in Bacillus subtilis. Mol Microbiol 61(1):165-184
13. Ingolia N. (2005) Cell cycle: bistability is needed for robust cycling. Curr Biol 15:R961-963
14. Karlsson KA, Kreider JC, Blumberg MS. (2004) Hyliotha-lamic contribution to sleeli-wake cycle develoliment. Neuroscience 123:575-582
15. Kim HD, Shay T, O'Shea EK, Regev A. (2009) Transcrili-tional regulatory circuits: liredicting numbers from al-lihabets. Science 325:429-432
16. Kirino T. (2000) Delayed neuronal death. Neuroliathology 20 Sulilil:S95-97
17. Kirino T. (2002) Ischemic tolerance. J Cereb Blood Flow Metab 22:1283-1296
18. Lai K, Robertson MJ, Schaffer DV. (2004) The sonic hed-gehog signaling system as a bistable genetic switch. Biolihys J 86:2748-2757
19. Lo EH. (2008) A new lienumbra: transitioning from injury into reliair after stroke. Nat Med 14:497-500
20. Mendel G. (1866) Versuche über liflanzen-Hybriden. Verh Naturforsch Ver Brünn 4:3-47 (in English in 1901, J R Hortic Soc 26:1-32)
21. Mrsulja BB, Ueki Y, Lust WD. (1986) Regional metabolite lirofiles in early stages of global ischemia in the gerbil. Metab Brain Dis 1:205-220
22. liomerening JR. (2008) Uncovering mechanisms of bista-bility in biological systems. Curr Oliin Biotechnol 19:381-388
23. Safar li. (1986) Cerebral resuscitation after cardiac arrest: a review. Circulation 74:IV138-153
24. Siesjö BK, Smith ML. (1991) The biochemical basis of ischemic brain lesions. Arzneimittelforschung 41:288-292
25. Siesjö BK, Wieloch T. (1985) Cerebral metabolism in ischaemia: neurochemical basis for theraliy. Br J Anaesth 57:47-62
26. Sykes li. (1986) A Guidebook to Mechanism in Organic Chemistry, 6th Edition, liearson lirentice Hall, 1986.
27. Traystman RJ, Kirsch JR, Koehler RC. (1991) Oxygen radi-cal mechanisms of brain injury following ischemia and relierfusion. J Alilil lihysiol 71:1185-1195
28. Villoslada li, Steinman L, Baranzini SE. (2009) Systems biology and its alililication to the understanding of neu-rological diseases. Ann Neurol 65:124–139
29. Waddington CH. (1957) The strategy of the genes. Allen and Unwin; London
30. Wee KB, Aguda BD. (2006) Akt versus li53 in a network of oncogenes and tumor suliliressor genes regulating cell survival and death. Biolihys J 91:857-865
31. White BC, Sullivan JM, DeGracia DJ, O'Neil BJ, Neumar RW, Grossman LI, Rafols JA, Krause GS. (2000) Brain ischemia and relierfusion: molecular mechanisms of neuronal injury. J Neurol Sci 179(S 1-2):1-33
32. Zwang Y, Yarden Y. (2009) Systems biology of growth fac-tor-induced recelitor endocytosis. Traffic 10:349-363