Accelerated and reduced-dose imaging: using undersampled acquisition and constrained reconstruction

¹Department of Medical Physics, University of Wisconsin–Madison, Madison, WI 53705, USA

Corresponding Author:

Sean Fain
Department of Medical Physics
University of Wisconsin–Madison
1111 Highland Avenue, Madison, WI 53705, USA
Tel: +1 608 263 0090
Fax: +1 608 265 9840
E-mail: sfain@wisc.edu

Abstract

Keywords

compressed sensing ▪ constrained reconstruction ▪ CT ▪ highly constrained projection reconstruction ▪ MRI ▪ PET ▪ radiation dose

Innovations in medical imaging continue to push the limits of engineering, for example the expansion in detector rows for x-ray CT [1] with dual energy sources [2], and the push to 128 parallel receive channels for MRI [3,4]. While these hardware innovations are impressive in their ability to accelerate acquisition speed and improve spatial resolution (e.g., acquisition of the entire heart within 50 ms and respiratory imaging of whole lung every 620 ms), they raise the cost and complexity of medical technology substantially. There has been a quieter, less glamorous revolution in the world of mathematics that has the potential to drive similar improvements in image acquisition speed without any or with minimal additional hardware requirements. The revolution is driven by compressed sensing (CS) theory and more generally ‘constrained’ reconstruction. While aspects of sparse mathematical transforms have been used empirically for years, for example JPEG image compression [5] and expectationmaximization image reconstruction [6], new approaches are emerging on a stronger theoretical footing and are driving radical and inexpensive improvements in acquisition speed in MRI and radiation dose reduction in x-ray CT.

A cornerstone of digital imaging is the Shannon-Nyquist sampling theorem [7]. The theorem states that a signal can be reconstructed exactly if sampled at twice its maximum frequency component – the so-called Nyquist sampling rate. Over the past decade, there has been growing empirical and theoretical work supporting the hypothesis that significant undersampling can be tolerated in certain applications. Many of the empirical developments were pioneered in information theory for applications in ‘lossy’ image and data compression algorithms that exploit psychovisual redundancy, such as the JPEG and MPEG algorithms [5]. In medical imaging, undersampled image acquisition strategies evolved in MRI, mostly in high contrast to noise applications, such as magnetic resonance angiography [8] and cardiac MRI [9,10], that achieve good image quality with easily tolerated artifacts for sampling rates 4–50-times below the Nyquist rate depending on the application. Many of these empirical methods could be understood in terms of imposing ‘data constraints’ that limit possible solutions for the reconstructed image spatially or temporally based on redundancies in the image series through space and time. However, these approaches lack a clear theoretical underpinning that defines the conditions for accurate image restoration in different applications and signal conditions.

Constrained reconstruction methods that accelerate acquisition speed by factors of 5–50-times have recently gained a strong theoretical foundation. In general, reconstruction of an N by N image would require solving a system of N² equations; however, if the image is sparse and the number of actual unknowns is S, then the problem size can be substantially reduced requiring only S equations. While many medical applications deal with sparse images, it is typically not known a priori which values of the image matrix are significant. Therefore, in reality, specially designed sampling schemes and more samples are needed. CS theory guarantees image reconstruction from O(S log(N)) randomly acquired samples. Alternatively, prior images or images integrated over a long time interval of a dynamic series can be used to determine which samples are most relevant. Novel combinations of these concepts of random sampling, image sparsity and constraining images have led to two lines of development.

The first set of related methods, largely but not exclusively based on radial acquisition geometry, exploit sparsity in the spatial-temporal image domain for dynamic imaging applications and are known as highly constrained projection reconstruction (HYPR) methods [11–13]. The second set of methods is based on CS theory [14,15] and exploits image sparsity in a mathematical transformation domain, for example, wavelet or finite difference transformation [16–18]. Both approaches have stimulated vibrant research that has led to rapid translation of these methods in MRI, CT and even PET for applications in dynamic imaging, x-ray dose reduction and improved kinetic modeling in PET [19].

Applications

MRI is particularly well suited to constrained reconstruction methods. This is largely a result of the flexibility of image data acquisition in the spatial frequency domain, where trajectory and sampling order can be directly controlled by modulating the strength and speed of the encoding magnetic field gradients. However, this also makes conventional MRI a slow imaging technique compared with ultrasound and CT, especially in body and cardiac applications where the need for accelerated acquisition to freeze motion is paramount. There are inherent hardware and physiologic limitations (e.g., nerve stimulation) on the strength and speed of the magnetic field gradients. The advent of multiple receiver channels has enabled parallel imaging methods that improve acquisition speed by factors of two to six. However, acceleration with parallel imaging is still insufficient for fully visualizing many dynamic applications and significantly degrades the signal-to-noise ratio (SNR), especially at accelerations greater than four.

A wide array of methods for increasing data acquisition efficiency in MRI using undersampling and constrained reconstruction are being used to obtain more robust dynamic MRI capabilities. Applications using HYPR or CS in MRI are being applied to imaging of cardiac wall motion [18], coronary artery imaging, peripheral and cranial magnetic resonance angiography [11,20], pediatric imaging [21], cardiac perfusion [22] and interventional catheter tracking [23]. Functional MRI applications where data acquisition speed is limiting, such as organ perfusion, diffusion tensor imaging, spectroscopic imaging [24] and blood oxygen level-dependent contrast are challenging emerging applications for constrained reconstruction approaches [19], as the data are typically less sparse in the image domain for these applications [12]. Similarly, emerging techniques that depend on short-lived hyperpolarized contrast agents, hyperpolarized gases [25,26] and metabolites [27] for example, require both high demand on data acquisition efficiency and quantitative accuracy to capture physiologic processes, such as tissue perfusion [12,13,28], lung ventilation [25] and cancer metabolism [27].

“Innovations in medical imaging continue to push the limits of engineering, for example the expansion in detector rows for x-ray CT … with dual energy sources … and the push to 128 parallel receive channels for MRI.”

Applications to CT and PET also share temporal correlation in dynamic image applications that can be exploited to constrain reconstruction. For MRI, speed of acquisition is the challenge, whereas for x-ray CT applications radiation dose is the limiting factor, especially in high-dose applications such as perfusion and fluoroscopy. Undersampling in the sense described previously for MRI would require changes in hardware, for example, pulsed x-ray sources to reduce number of sampled angles. However, exploiting temporal redundancy in dynamic settings can still be readily performed by integrating multiple frames of image data over a dynamic time course and then using constrained reconstruction to obtain quantitative kinetic information. Perfusion applications have already been demonstrated in a pig model using the prior image-constrained CS algorithm [29]. For example, dose reductions of factors of six to ten have been demonstrated for angiography [30] and perfusion imaging applications using HYPR [31] without any changes to scanner hardware. For coronary artery imaging, a factor of two improvement in temporal resolution was achieved by using an incomplete range of projection angles to reconstruct shorttime frame cardiac windows without additional detectors or increased gantry speed [32].

Similar approaches are taken to obtain improved SNR for modeling of tracer kinetics in PET [19]. As with HYPR approaches in MRI, a long time window scan is used to constrain signal values, while data consistency is enforced over a narrow time window to improve both the temporal resolution and SNR. This approach should improve modeling of conventional tracers and enable the modeling of tracers with longer half-lives and reduced photon counts – again without any hardware modifications.

Challenges

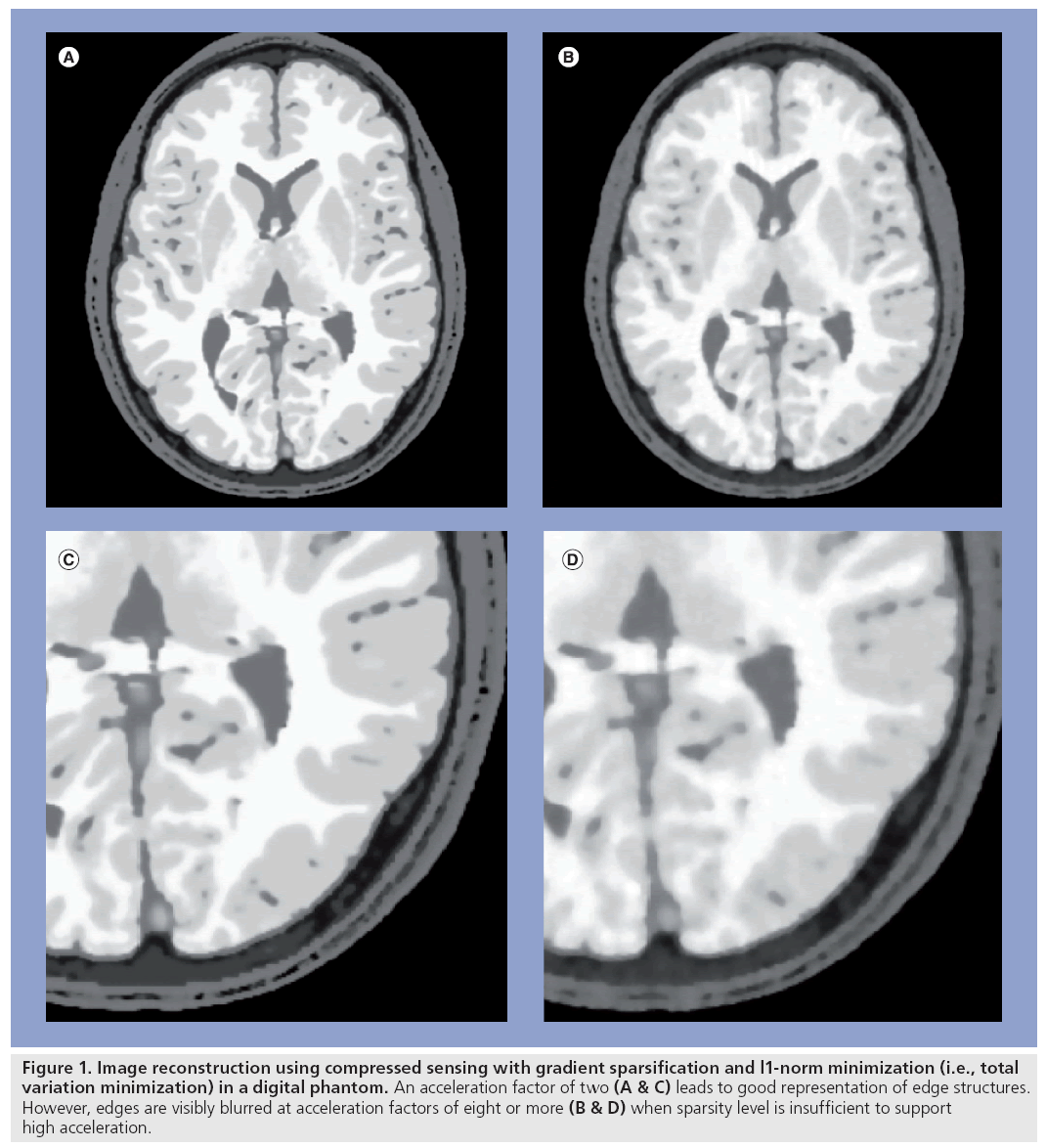
The challenges of quantitative accuracy place limits on the achievable acceleration using constrained reconstruction methods (Figure 1). In MRI, this limitation has motivated the combination of HYPR and CS methods with parallel acquisition [28,33–35] so as to obtain high accelerations by offsetting the limitations of the two techniques. For example, the reduced SNR resulting from higher parallel imaging accelerations can be offset by constrained reconstruction to improve SNR, thus preserving image quality while achieving higher net acceleration factors [21]. A similar approach has been used to improve quantitative accuracy of contrast kinetics in cardiac perfusion applications [28].

Figure 1: Image reconstruction using compressed sensing with gradient sparsification and l1-norm minimization (i.e., total variation minimization) in a digital phantom. An acceleration factor of two (A & C) leads to good representation of edge structures. However, edges are visibly blurred at acceleration factors of eight or more (B & D) when sparsity level is insufficient to support high acceleration.

The rapid proliferation of constrained imaging approaches and the wide array of methods in use by different research groups has added further uncertainty as to which methods work best. To identify the ‘winners,’ what is most needed within the research community are metrics of performance that reflect errors in temporal kinetics, structural artifacts and image contrast that capture relevant features of diagnosis for a given application. For example, root mean square difference is widely used as an error measure because of its simplicity, which outweighs its limited ability to capture the relative coherence of artifacts that matter most to the radiologist’s perception of image quality and diagnostic value. Meaningful objective performance metrics are even more important for validating emerging functional imaging techniques where quantitative accuracy is critical to the application, for example magnetic resonance diffusion, T₂*, spectroscopic imaging, and both CT and MRI perfusion imaging.

Future perspective

At present it seems certain that constrained reconstruction methods will advance dynamic imaging applications because they satisfy a clear need for improved temporal resolution and reduced x-ray dose in MRI and CT, respectively. Despite the clinical need, clinical validation studies are required to quantify the added diagnostic value of accelerated imaging using constrained reconstruction. The relevance of constrained reconstruction to structural imaging is less certain because the clinical need is less apparent, although reducing overall scan time for MRI procedures will have clear cost benefits in reducing total examination time, motion artifacts, and patient tolerance in pediatric and inpatient studies. Clinical studies that assess the impact on diagnosis of these applications will also be central to their acceptance by the radiological community. In MRI, the success of translational research efforts will depend on the added value in terms of improved access (e.g., pediatric studies), reduced examination time and hardware costs. For CT applications, reduced x-ray dose in the face of increased public concern over x-ray radiation exposure will have a significant impact if diagnostic quality can be maintained.

Financial & competing interests disclosure

SB Fain receives research support and serves as a consultant to GE Healthcare for development and application of hyperpolarized MRI contrast agents, and also receives funding from the NIH. The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed.

No writing assistance was utilized in the production of this manuscript.

References

1. Mori S, Kondo C, Suzuki N, Hattori A, Kusakabe M, Endo M: Volumetric coronary angiography using the 256-detector row computed tomography scanner: comparison in vivo and in vitro with porcine models. Acta Radiol. 47, 186–191 (2006).
2. Flohr TG, McCollough CH, Bruder H et al.: First performance evaluation of a dual-source CT (DSCT) system. Eur. Radiol. 16, 256–268 (2006).
3. Hardy CJ, Hardy CJ, Giaquinto RO et al.: 128-channel body MRI with a flexible high-density receiver-coil array. J. Magn. Reson. Imaging 28, 1219–1225 (2008).
4. Adriany G, Auerbach EJ, Snyder CJ et al.: A 32-channel lattice transmission line array for parallel transmit and receive MRI at 7 tesla. Magn. Reson. Med. 63, 1478–1485 (2010).
5. Taubman DS, Marcellin MW: JPEG2000: Image Compression Fundamentals, Standards, and Practice. Kluwer Academic Publishers, MA, USA (2002).
6. Shepp LA, Vardi Y: Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1, 113–122 (1982).
7. Oppenheim AV, Schafer RW: Digital Signal Processing. Prentice-Hall, NJ, USA (1975).
8. Peters DC, Korosec FR, Grist TM et al.: Undersampled projection reconstruction applied to MR angiography. Magn. Reson. Med. 43, 91–101 (2000).
9. Tsao J, Boesiger P, Pruessmann KP: k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn. Reson. Med. 50, 1031–1042 (2003).
10. Kozerke S, Tsao J: Reduced data acquisition methods in cardiac imaging. Top. Magn. Reson. Imaging 15, 161–168 (2004).
11. Mistretta C, Wieben O, Velikina J et al.: Highly accelerated MRI using undersampled acquisition and HYPR processing. Med. Phys. 34, 2598 (2007).
12. O’Halloran RL, Wen ZF, Holmes JH, Fain SB: Iterative projection reconstruction of time-resolved images using highlyconstrained back-projection (HYPR). Magn. Reson. Med. 59, 132–139 (2008).
13. Johnson KM, Velikina J, Wu Y, Kecskemeti S, Wieben O, Mistretta CA: Improved waveform fidelity using local HYPR reconstruction (HYPR LR). Magn. Reson. Med. 59, 456–462(2008).
14. Candes EJ, Romberg J, Tao T: Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory 52, 489–509 (2006).
15. Donoho DL: Compressed sensing. IEEE Trans. Inform. Theory 52, 1289–1306 (2006).
16. Lustig M, Donoho DL, Santos JM, Pauly JM: Compressed sensing MRI. IEEE Signal Process Mag. 25, 72–82 (2008).
17. Lustig M, Donoho D, Pauly JM: Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).
18. Gamper U, Boesiger P, Kozerke S: Compressed sensing in dynamic MRI. Magn. Reson. Med. 59, 365–373 (2008).
19. Mistretta CA: Undersampled radial MR acquisition and highly constrained back projection (HYPR) reconstruction: potential medical imaging applications in the post-nyquist era. J. Magn. Reson. Imaging 29, 501–516 (2009).
20. Velikina JV, Johnson KM, Wu Y, Samsonov AA, Turski P, Mistretta CA: PC HYPR flow: a technique for rapid imaging of contrast dynamics. J. Magn. Reson. Imaging 31, 447–456 (2010).
21. Vasanawala SS, Alley MT, Hargreaves BA, Barth RA, Pauly JM, Lustig M: Improved pediatric MR imaging with compressed sensing. Radiology doi:10.1148/ radiol.10091218 (2010) (Epub ahead of print).
22. Ge L, Kino A, Griswold M, Mistretta C, Carr JC, Li D: Myocardial perfusion MRI with sliding-window conjugate-gradient HYPR. Magn. Reson. Med. 62, 835–839 (2009).
23. Schirra CO, Weiss S, Krueger S et al.: Toward true 3D visualization of active catheters using compressed sensing. Magn. Reson. Med. 62, 341–347 (2009).
24. Wang K, Du J, O’Halloran R et al.: Ultrashort TE spectroscopic imaging (UTESI) using complex highly-constrained backprojection with local reconstruction (HYPR LR). Magn. Reson. Med. 62, 127–134 (2009).
25. Holmes JH, O’Halloran RL, Brodsky EK et al.: Three-dimensional imaging of ventilation dynamics in asthmatics using multiecho projection acquisition with constrained reconstruction. Magn. Reson. Med. 62, 1543–1556 (2009).
26. O’Halloran RL, Holmes JH, Wu YC, Alexander A, Fain SB: Helium-3 MR q-space imaging with radial acquisition and iterative highly constrained backprojection. Magn. Reson. Med. 63, 41–50 (2010).
27. Hu S, Lustig M, Balakrishnan A et al.: 3D compressed sensing for highly accelerated hyperpolarized 13C MRSI with in vivo applications to transgenic mouse models of cancer. Magn. Reson. Med. 63, 312–321 (2010).
28. Otazo R, Kim D, Axel L, Sodickson DK: Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn. Reson. Med. doi:10.1002/mrm.22463 (2010) (Epub ahead of print).
29. Chen GH, Tang J, Leng S: Prior image constrained compressed sensing (PICCS). Proc. Soc. Photo Opt. Instrum. Eng. 6856, 685618 (2008).
30. Supanich M, Tao Y, Nett B et al.: Radiation dose reduction in time-resolved CT angiography using highly constrained back projection reconstruction. Phys. Med. Biol. 54, 4575–4593 (2009).
31. Liu X, Primak AN, Krier JD, Yu L, Lerman LO, McCollough CH: Renal perfusion and hemodynamics: accurate in vivo determination at CT with a 10-fold decrease in radiation dose and HYPR noise reduction. Radiology 253, 98–105 (2009).
32. Chen GH, Tang J, Hsieh J: Temporal resolution improvement using PICCS in MDCT cardiac imaging. Med. Phys. 36, 2130–2135 (2009).
33. Liang D, Liu B, Wang J, Ying L: Accelerating SENSE using compressed sensing. Magn. Reson. Med. 62, 1574–1584 (2009).
34. Wang K, Holmes J, Busse R et al.: Interleaved variable density sampling with ARC parallel imaging and cartesian HYPR for dynamic MR angiography. Presented at: The 18th Annual Meeting of ISMRM. Stockholm, Sweden 1–7 May 2010 (Abstract 352).
35. Velikina J, Samsonov A: HYPR-L0: a hybrid technique for CE MRA with extreme data undersampling factors. Proc. ISMRM 276 (2009).