Towards a dynamical network view of brain ischemia and reperfusion. Part IV: additional considerations

*Corresponding Author:

Donald J. DeGracia, Ph.D.
Department of Physiology, Wayne State University, 4116 Scott Hall
540 East Canfield Ave., Detroit, MI 48201, U.S.A
Phone 313-577-6745
Fax 313-577-5494
E-mail: ddegraci@med.wayne.edu

Abstract

The general failure of neuroprotectants in clinical trials of ischemic stroke points to the possibility of a fundamen-tal blind spot in the current conception of ischemic brain injury, the “ischemic cascade”. This is the fourth in a series of four papers whose purpose is to work towards a revision of the concept of brain ischemia by applying network concepts to develop a bistable model of brain ischemia. Here we consider additional issues to round out and close out this initial presentation of the bistable network view of brain ischemia. Initial considerations of the network architecture underlying the post-ischemic state space are discussed. Network and differential equa-tion models of brain ischemia are compared. We offer a first look at applying the bistable model to focal cere-bral ischemia. The limitations of the present formulation of the bistable model are discussed. This work con-cludes with a series of questions by which to direct future efforts.

Keywords

Bistability; brain ischemia and reperfusion; focal cerebral ischemia; postischemic state space

Abbreviations

Akt     pro-survival kinase

CBF     cerebral blood flow

CD     the attractor for cell death

D     delayed neuronal death region of post-ischemic state space

Danger zone     points to the right of the separatrix in the post-ischemic state space

DM     effective total ischemia-induced damage

dmi     variable representing a specific damage mechanism

DMSO     dimethyl sulfoxide

H     homeostatic region of post-ischemic state space

HSP70     70kDa inducible heat shock protein

I     the amount of ischemia

N     necrotic region of post-ischemic state space

P     preconditioning region of post-ischemic state space

ROS     reactive oxygen species

S     the attractor for the steady-state phenotype of a neuron

Safe zone     points to the left of the separatrix in the post-ischemic state space

SR     effective total ischemia-induced stress response capacity

sri     variable representing a specific stress response

TF     transcription factor

TN     threshold of necrosis

Introduction

In this 4th paper of the series, we finish with discussions that round out and complete our presentation. We provide some tentative thoughts about the actually network that underlies, or gives rise to, the postischemic state space. We next compare the network model to differential equation-based models of brain ischemia. We then briefly discuss how stroke or focal ischemia looks through the lens of the bistable model. We end discussing some limitations of our admittedly incomplete bistable model and pose some obvious questions to guide future work.

The network underlying the post-ischemic state space

It is seemingly ironic that one of the last topics we consider is the actual network that gives rise to the post-ischemic state space. Usually, state space models follow after the network has been defined. Consider for example the transcriptional network of E. coli (Shen-Orr et al 2002). Painstaking systematic work identified the interactions of all transcription factors with their respective promoters, providing the nodes, their inputs and targets: in short, the network architecture (Mori 2004; Seshasayee et al 2006). Then, dynamical simulations of the network, based on the real kinetics of node interactions (Ronen et al 2002), reveal the state space (Smolin et al 2000).

Properties of the state space such as attractors, bistability, or other landscape features, are said to be emergent properties arising from the network dynamics.

It is thus no exaggeration that we worked backwards developing the bistable model of brain ischemia. To briefly recap: In the 2nd paper we constructed the state space from the empirical knowledge of global brain ischemia. We next said that the state space resulted from the competition between DM and SR, providing two mutually antagonistic variables whose input functions [DM = f(I) and SR = g(I)] should generate a state space displaying bistability. In the 3rd paper, we framed DM and SR as aggregate or ensemble variables made up of the many dmi and sri. The Wieloch sandwich model provided superposition as a first pass at a mathematical relationship between DM/dmi and SR/sri. However, we pointed out that if the many dmi and sri are posited to be nodes in a network, then superposition is a logical impossibility because network nodes are not independent. Thus, we do not yet know the mathematical functions, let’s call them h and i, such that DM = h(dmi) and SR = i(sri). While we do not yet know the form of h and i, they must stem from the architecture of the network underlying the state space.

Let us therefore consider the network by first explicitly stating: the nodes of the network underlying the postischemic state space - the individual dmi and sri, - are in fact the many elements of the ischemic cascade. All individual molecular elements of damage (dmi) or stress response (sri) activated in neurons by ischemia, taken in toto, form the universe of possible nodes. Then, the functional linkages between these nodes would give us the network architecture. We know the ischemic cascade consists of many different molecular pathways, the elements of which we have functionally classified as contributing either to damaging the cell (dmi) or helping the cell survive (sri).

Within this binary classification scheme we can readily imagine how specific dmi or sri would cluster via their related molecular pathways. For example, the molecular pathways of the heat shock response would form a cluster of related sri nodes. The heat shock response is thought to be activated by the formation of protein aggregates (DeGracia and Hu 2007). The pathways by which protein aggregates form would then cluster as related dmi nodes. The heat shock (sri) and protein aggregate (dmi) nodes would interact, forming a larger cluster of interacting nodes. Similar logic can be applied to other antagonistic yet interacting pathways found after brain ischemia: free radical damage/antioxidant defenses, proapoptotic/antiapoptotic pathways, energy depletion/energy conservation pathways, Ca2+ dysregulation/Ca2+ buffering pathways and so on.

While we cannot yet determine the network at a high resolution nodetonode scale, we can at least envision the course, low resolution architecture of the network. The network would be expected to consist of many clusters of densely connected nodes, where each such cluster is one of the familiar molecular pathways of the ischemic cascade. Within such a cluster, any given node would have only has a small number of connections, reflecting the local linearity of the pathways within the cluster. However, the many clusters would be linked by a much smaller number of nodes that form hubs amongst the many clusters.

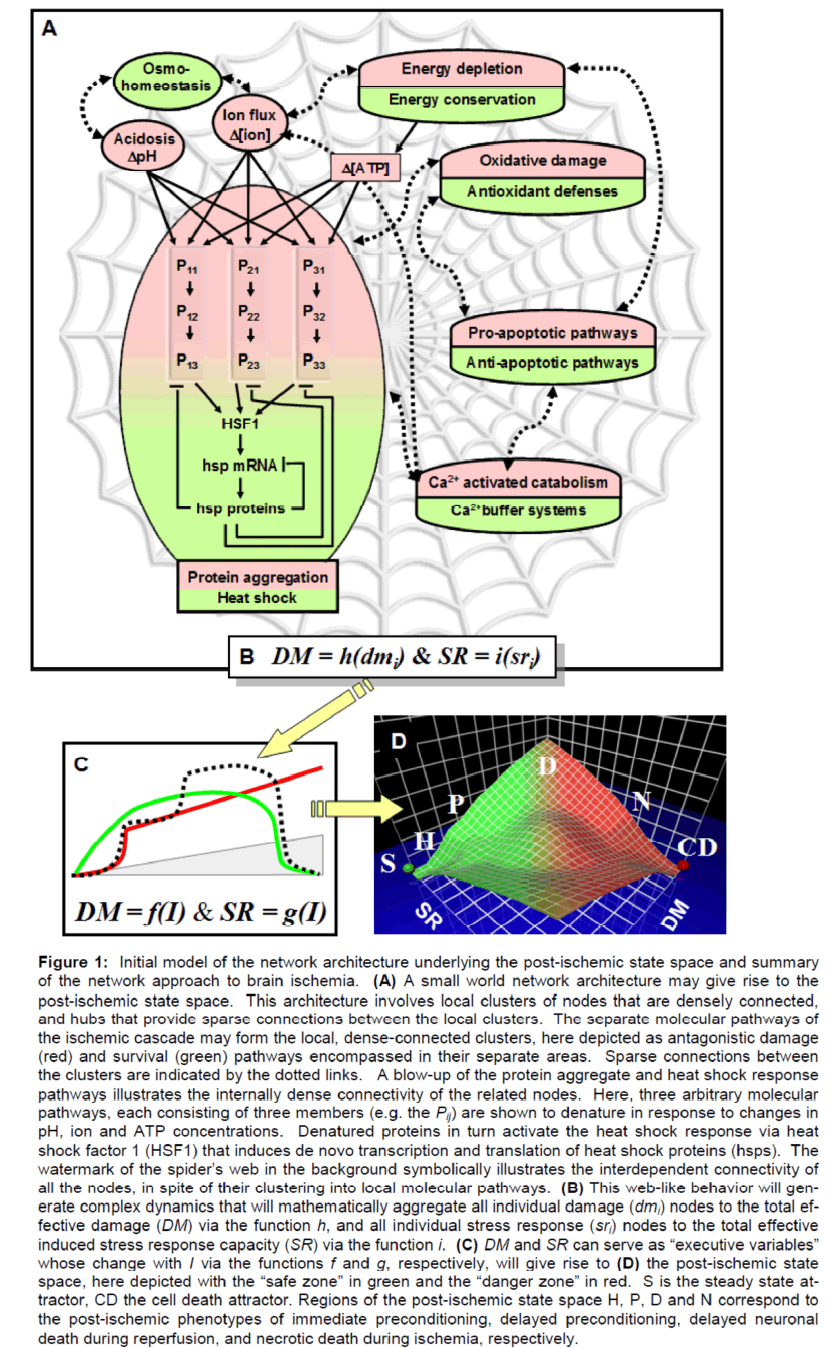
This low resolution architecture is illustrated in Figure 1, which is by no means meant to be complete, but simply representative. Each oval represents a local, denselyconnected cluster in terms of specific antagonistic damage (red) and stress response (green) pathways familiar to aficionados of brain ischemia. The damage elements (dmi) are in red and the protective elements (sri) are in green. The cluster for the protein aggregates/heat shock response is blownup to illustrate some of the dense connectivity of the nodes within this particular cluster. While the other clusters are not so depicted, the reader can imagine the complex molecular pathways contained within each of the clusters.

Figure 1: Initial model of the network architecture underlying the postischemic state space and summary of the network approach to brain ischemia. (A) A small world network architecture may give rise to the postischemic state space. This architecture involves local clusters of nodes that are densely connected, and hubs that provide sparse connections between the local clusters. The separate molecular pathways of the ischemic cascade may form the local, denseconnected clusters, here depicted as antagonistic damage (red) and survival (green) pathways encompassed in their separate areas. Sparse connections between the clusters are indicated by the dotted links. A blowup of the protein aggregate and heat shock response pathways illustrates the internally dense connectivity of the related nodes. Here, three arbitrary molecular pathways, each consisting of three members (e.g. the Pij) are shown to denature in response to changes in pH, ion and ATP concentrations. Denatured proteins in turn activate the heat shock response via heat shock factor 1 (HSF1) that induces de novo transcription and translation of heat shock proteins (hsps). The watermark of the spider’s web in the background symbolically illustrates the interdependent connectivity of all the nodes, in spite of their clustering into local molecular pathways. (B) This weblike behavior will generate complex dynamics that will mathematically aggregate all individual damage (dmi) nodes to the total effective damage (DM) via the function h, and all individual stress response (sri) nodes to the total effective induced stress response capacity (SR) via the function i. (C) DM and SR can serve as “executive variables” whose change with I via the functions f and g, respectively, will give rise to (D) the postischemic state space, here depicted with the “safe zone” in green and the “danger zone” in red. S is the steady state attractor, CD the cell death attractor. Regions of the postischemic state space H, P, D and N correspond to the postischemic phenotypes of immediate preconditioning, delayed preconditioning, delayed neuronal death during reperfusion, and necrotic death during ischemia, respectively.

There is a formal name for such architecture; it is called a small world network. Small world networks have been found to be highly prevalent in nature: in cognitive processing (Palva et al 2010), in social networks (Zhang and Zhang 2009), in the structure of the World Wide Web (Louzoun et al 2006), and in gene transcriptional networks (Ma'ayan 2009), to name a few examples. While there are technical criteria which designate a network architecture as being of the small world variety (Zhang and Zhang 2009), we do not attempt that level of precision here. Instead, the intuitive considerations discussed above amount to hypothesizing that the many elements of the ischemic cascade form a small world network.

For argument’s sake, let us assume the elements of the ischemic cascade indeed form a small world architecture and consider an important implication. Again, there are many clusters that are internally densely connected, each corresponding to a familiar pathway of the ischemic cascade. But these many clusters are sparsely connected together by hub nodes. The sparse connections between denselyconnected clusters are indicated by the dashed links in Figure 1. It is the sparse connections between clusters that nullify the assumption of superposition. If each denselyconnected cluster (e.g. molecular pathway) operated in complete isolation from all others, then each pathway would indeed be independent, and superposition would apply. But the sparse connections amongst the denselyconnected clusters make them interdependent. A change in one cluster will propagate, to some extent or another, via the sparse connections through all of the clusters. This is insinuated by the web in the background, indicating the complex weblike behavior of the chemical changes induced by ischemia. Hence some mathematical relationship other than superposition must describe the integrated behavior of the clusters (pathways). That is, DM and SR are not simply linear summations of their respective dmi and sri. The complex dynamic interactions of all the dmi and sri would be the basis of calculating DM and SR from the network. Clearly, this would be a very complex set of formulas. But complex systems theory posits that a multitude of interconnected pathways can collapse to a lowdimensional outcome, which we posit to be the twodimensional competition between DM and SR, leading in turn to the only two cellular outcomes after ischemia: life or death.

Tying it all together for the moment

Figure 1 also serves to tie together and summarize the whole of our network approach as it presently stands. While we built this in the backwards order, we summarize it in the forward order. We posit that the changes induced in brain cells by ischemia are nodes in a network of interconnected molecular changes, some of which damage (dmi), some of which protect (sri) the cell. Since there are only two categories of changes that affect outcome, we can aggregate these changes, albeit in presently unknown forms represented by the functions h and i, and speak of total damage (DM) and total protective capacity (SR). In this fashion, instead of focusing on every single node (e.g. every single ischemiainduced change), we can substitute DM and SR as “executive” or “summary” variables. We can then think about how the relative magnitudes of DM and SR change with the amount of ischemia, I, via the input functions DM = f(I) and SR = g(I). Then, by emulating approaches validated in other disciplines (as discussed in the preceding papers), we can use the functions f and g to generate a state space whose main emergent property is bistability. We then map the bistable state space to the only two possible outcomes following brain ischemia: survival (S) or cell death (CD). Along with bistability, we anticipate that the functions f and g will produce a state space landscape that contains the features associated with the metastable postischemic phenotypes H, P, D and N.

Within the context of this bird’s eye view summary, we present a few miscellaneous thoughts. The first involves clarifying the intent of the present model, followed by two metaphors that hopefully can impart a more “down to earth” air to the entire network approach to brain ischemia.

First, while a network of some sort must underlie DM and SR, the intent of the bistable model is decidedly not to find the detailed network. While this is possible in principle, the whole point of reducing the complexity of the ischemic cascade network to the functions DM = f(I) and SR = g(I) is to explore the possibility that practical approaches to understanding brain ischemia can be developed without reference to every single underlying molecular event. Workers in the area of brain ischemia must be alarmed at the rate with which new molecular pathways have continued to be added to the ischemic cascade. What began as a relatively simple model of Ca2+ overload (Siesjö 1981) has grown exponentially to encompass essentially every aspect of neuronal cellular biology. The undisciplined application of the “plus/minus” strategy coupled with the (mostly implicit) assumption of superposition has caused the ischemic cascade concept to explode out of control so that it more and more resembles a Tower of Babel.

Therefore, a very practical aspect of the network approach is to find a functional substitute for all of this seemingly unrelated complexity. That substitute is found in the concepts of DM and SR. If the functions f and g can be empirically determined, then the effects of brain ischemia can be expressed in terms of state spaces. It then may be possible to develop successful therapeutics based solely on the state space concept, without any dependency on any specific set of detailed changes at the molecular level. Again, given the expectation of finding some magical cell death pathway X, the idea that something practical can be done with no reference to specific details must seem vacuous at first hearing. To make the network concepts more palatable, we wrap up this section with two simple metaphors that hopefully will not only clarify the concepts, but suggest directions by which concrete approaches might materialize.

The money metaphor. We can compare a cell that has experienced ischemia to a rundown house. Imagine we own a run down, dilapidated house; its windows are broken, the electrical wiring is fried, there are broken pipes and holes in the walls. But this house is not so run down it cannot be repaired. Each form of damage in the house is analogous to the different forms of cell damage ischemia causes in a cell; the many dmi: membrane damage, organelle damage, signaling alterations, and so on. Now, each form of damage in the house will require some type of specialized knowledge to repair. We need a plumber to fix the pipes, an electrician to fix the wiring, a carpenter to fix the walls and windows. Again, this is analogous to the many stress responses (sri) the cell invokes to repair itself in response to ischemic damage. Even though we need to use different types of exper-tise to fix the house, there is one common basis upon which it will get fixed: money. In real terms, there will be a specific dollar amount associated with every repair. On this basis then, all the forms of damage can be added together and the total cost to fix the house will be X dollars. In these terms, we do not need to know anything about the specific details. The total dollar amount, X, is proportional to the total amount of damage.

Now, the analogy continues because anybody that has ever hired someone to do repairs in their house knows that the cost of repair is made up of two components, usually termed “materials” and “labor”. The real cost of materials is often much less than the total repair costs because of the labor costs. Furthermore, the cost of labor is a function of who does the job, not the degree of damage. A licensed contractor costs much more than someone without a license, who in turn costs much more than having a friend help you do the repair in exchange for beer and pizza. Thus, the labor costs more reflect the capacity of the skills brought to bear on the repairs. Hiring an experienced contractor who routinely builds highrise buildings is bringing more capacity to the repair job than hiring say, someone who only hangs drywall and paints.

Thus, the two costs involved in fixing the house can be readily separated. The first cost is the material cost, which will be precisely correlated to the actual damage that needs to be repaired. The variable DM is analogous to total materials costs. DM is a measure of the total actual damage a cell experiences after ischemia. SR, on the other hand, is analogous to labor costs. SR reflects the total capacity the cell induces to carry out the repairs. It is possible that the cell induces a repair capacity that is much greater than what the actual damage merits. Hence we get surplus repair capacity, and a “preconditioned” phenotype. But just as with the house repair analogy, where both materials and labor can be put on an equal basis via money, there must be an analogous measure whereby DM, the total, but actual damage produced, can be directly compared to SR, which is the capacity brought to bear on fixing the damage. This is the “money metaphor”, and can serve as a very loose guide in converting the ideas expressed here into real and practical approaches. To convert the approach presented here to something real and concrete is predicated on finding empirical measures of DM and SR, and further, finding some basis, analogous to money in the home repair metaphor, by which DM and SR can be directly compared.

The web metaphor. The second metaphor is perhaps more standard when discussing networks, but should be said explicitly here, and especially in connection to the state spacederived concept of neuroprotection presented in the 3rd paper.

As Figure 1 illustrates, the complex network dynamics induced in brain cells by ischemia can be viewed as a web of interactions. The fallacy of thinking of the changes induced by ischemia as being a “cascade” is that this term implies a linear sequence of causation, and it is a term that derives from an implicitly pathwaysdriven approach to the problem. While time, as a variable, is fully expected to play a role in the four functions introduced here, f, g, h and i, the role of time in the dynamic behavior of the network is clearly much more complex than simply providing a linear x-axis to some linear sequence of events, as if with a series of dominos, one knocking down the next. If Brain Ischemia 1.0 gave us the “ischemic cascade”, then Brain Ischemia 2.0 gives us the “ischemic web.”

We can use the web metaphor to get an intuitive handle on the idea that a neuroprotectant is a perturbation of the postischemic state space. How do we visualize applying a neuroprotectant to this dynamic network? And how does this related to the concept of “specificity” and molecular pathways that so dominated the field at present? Simply stated, one can imagine applying force to a spider’s web. The applied force will propagate throughout the web structure. It doesn’t matter where on the web the force is applied; it will still propagate through the entire web. In this regard, “specificity” of drug action is analogous to touching different locations of the spider’s web. The action of some drug on some molecular pathway is more a measure of where on the web one has applied the force. But the force will still propagate throughout the web. It may well turn out that, unlike a spider’s web, where one “touches” (e.g. applies a drug or affects a specific cluster) the complex network induced by ischemia does make a difference. In that case, specificity would have shades of gray in terms of propagating through the network, and hence altering the state space. This is of course a very simple metaphor, but useful for helping shift out of the pathways mode of thinking of neuroprotection and into the network view of neuroprotection.

Having made these essentially closing comments about the bistable model of brain ischemia in its present form, we now close out this presentation with some broader issues that merit at least brief consideration.

Mathematical approaches to brain ischemia

The network approach is clearly a mathematical approach to brain ischemia. Here we discuss how the network approach compares to existing mathematical approaches to brain ischemia, which are essentially of the differential equation variety. A small handful of authors have presented mathematical models of brain ischemia. All the mathematical results are very interesting and should be more widely appreciated. We focus on work from Boissel’s group in France since this has been the main group producing such models over many years.

Boissel’s work involves simulations using differential equations, aimed at modeling the dynamics of elements of the ischemic cascade. They have, for example, done very nice simulations of changes in extracellular ion concentrations after simulated ischemia that produce spreading depression waves (Chapuisat et al 2008). The advantage of their approach is that sometimes unexpected things will pop out of the simulations that are either not something one would envision beforehand, or that describe a phenomena that is experimentally inaccessible. The modeling of glia and white matter mentioned in the 3rd paper is but one such example (Dronne et al 2007). These are of course very good things.

The main weakness of the differential equation approach is that it requires numbers that may not have been or cannot be experimentally measured such as specific binding, rate and equilibrium constants. When such numbers are missing, these types of simulations are dependent upon a technical necessity that one has to run the model over and over again making guesses at these numbers (Chapuisat et al 2008; Huang 2009). When the model behaves “as expected”, one then uses the resulting guessed numbers in further simulations. If such models are dependent upon acting “as expected” this perhaps weakens their perceived value.

These considerations also illustrate that differential equation models are dependent upon modeling something we already know is happening. In themselves they cannot really speak to causality; that needs to be known beforehand and then modeled. Perhaps this is why computer simulations aren’t treated more seriously in some quarters, because the simulations only reflect what was programmed into them. On the other hand, physicists use simulations all the time as important guides to designing experiments, checking experimental data and so on.

In contrast, network models provide a different type view on the system they model. As we have emphasized, networks models are not required to focus on the fine details of the system, and instead look for patterns in the system as a whole. These of course are the state space landscapes that provide a global view of the system. Further, these types of models are not necessarily dependant on physical parameters as are differential equations. In the GATA1/PU.1 example discussed in the 2nd paper, the real physical concentrations did not even need to be specified. Only the ratio of the concentrations was required, which is a dimensionless number. In general, network models are what have been termed “functional” or “qualitative”, meaning they are intended to capture the essential functions of the system as a whole (Huang 2009). In the GATA1/PU.1 system only the essential function, bistable control of phenotype, was modeled. This was not a model of binding interactions with dissociation constants or anything like that. This is precisely how we approached applying bistability to ischemia: the outcomes, the functions were sought to be modeled, and we focus on no specific details at all. Because of their intrinsic mathematics, network models can show selforganization, and indeed sometimes produce results that were completely unexpected beforehand via the emergent properties of the network.

In the final analysis, the two mathematical approaches are complimentary. Modeling with differential equations gives a finegrained, detailed look at a process. Networks give a systemwide view of the process. However, since we are talking about mathematical methods, they are not simply complementary but convergent. The individual nodes of the network can be modeled with differential equations, as can be the denselyconnected clusters (Alon 2006). What this means is that the issues such as the relationship between DM and SR and the individual dmi and sri can be approached by a convergence of differential equation modeling and network modeling. Basically, the differential equations are nested as nodes in the network such that the inputs to the nodes are the parameters for the differential equations. We anticipate such a convergence to increasingly complement purely empirical data.

Stroke and the bistable model

We now offer a few comments on focal ischemia from the point of view of the bistable model. Recall the bistable model was designed to describe complete global cerebral ischemia (CGI), and further to only apply to neurons. How can the ideas be carried over to focal ischemia? For the sake of simplicity in the following discussion, we will loosen our rigor slightly and talk about a given phenotype belonging to the brain tissue and not specifically just to a neuron.

In the bistable model of CGI, the brain is exposed to only one specific amount of ischemia, I. The brain is then pushed to the single phenotype corresponding to that I such that the brain is in H, or P, or D or N. Over time that phenotype will decay either to S or CD depending on I. However, as discussed in the 1st paper, focal ischemia contains different levels of CBF occurring in the same brain at the same time. Stated slightly differently, different volumes of tissue in the same brain are simultaneously experiencing different values of I. We therefore expect focal ischemia to simultaneously induce multiple postischemic phenotypes in the same brain.

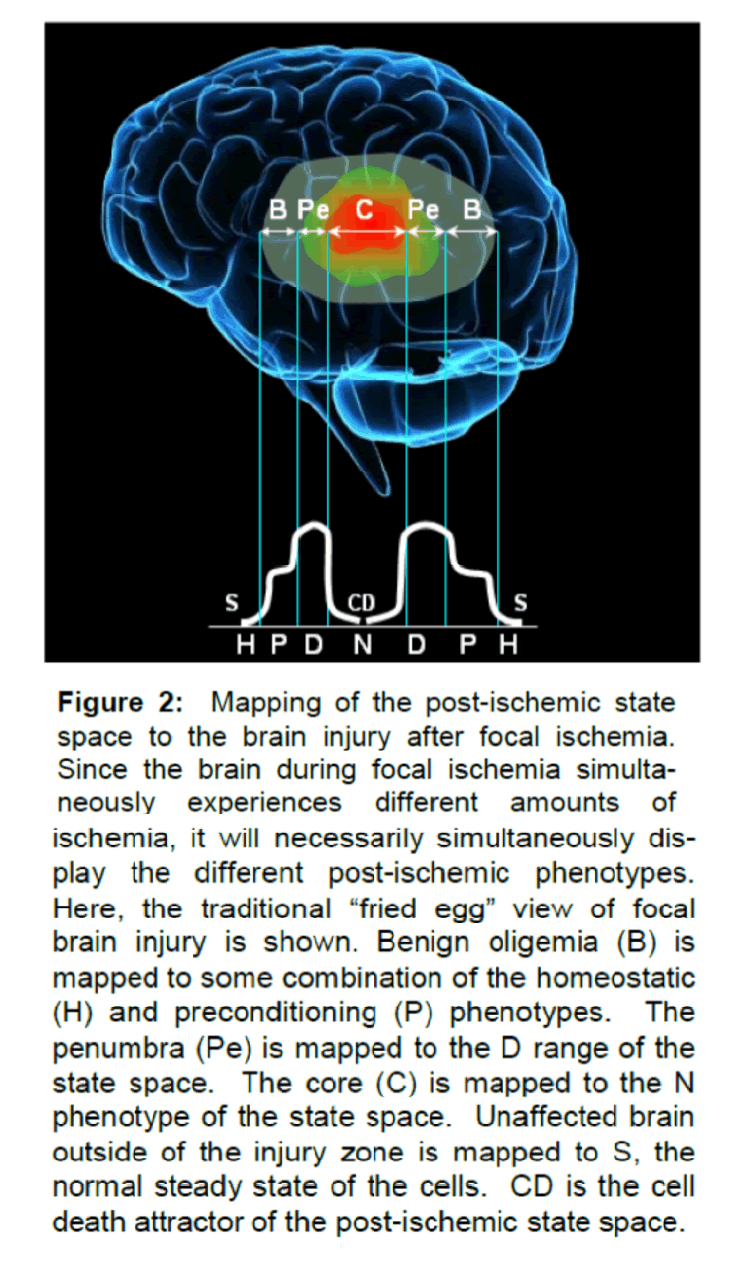
By way of example, let us make the crude assumption that the CBF gradient during a focal insult is continuous from 0% (at the point of obstruction) to 100% (sufficiently far from the obstruction) for a sufficient length of time. This would mean that all amounts of ischemia from I > 0 to I > TN are occurring simultaneously in the same brain. Therefore we would expect the appearance of all the phenotypes in the state space to occur simultaneously in the same brain (Figure 2). That is, there should be regions in the focal ischemic brain expressing the H, and P, and D and N phenotypes. The spatial localization of each phenotype would follow the ischemic gradient. If the brain after focal ischemia expresses all the phenotypes, this gives rise to something not found in a brain after CGI: the interactions of the phenotypes. Thus, focal ischemia gives rise to two additional layers of complexity as compared to global ischemia: the simultaneous presence of different phenotypes, and the interactions of the phenotypes amongst themselves.

Figure 2: Mapping of the postischemic state space to the brain injury after focal ischemia. Since the brain during focal ischemia simultaneously experiences different amounts of ischemia, it will necessarily simultaneously display the different postischemic phenotypes. Here, the traditional “fried egg” view of focal brain injury is shown. Benign oligemia (B) is mapped to some combination of the homeostatic (H) and preconditioning (P) phenotypes. The penumbra (Pe) is mapped to the D range of the state space. The core (C) is mapped to the N phenotype of the state space. Unaffected brain outside of the injury zone is mapped to S, the normal steady state of the cells. CD is the cell death attractor of the postischemic state space.

It is interesting to note that the bistable model would by itself predict discreet regions of distinctly identifiable phenotypes in a brain after focal ischemia. It is well known that this is the case, but we did nothing intentionally to make a model of outcome following focal ischemia. We simply applied the bistable model of CGI to the case where there is a CBF gradient in the brain. The CBF gradient gives rise to different amounts of ischemia in the same brain, and the bistable model says we should expect multiple phenotypes.

It is widely appreciated that at least four definable areas (technically, volumes) can be found in a brain after focal ischemia: the core, the penumbra, the area of benign oligemia, and the unaffected brain (Warach 2001). We readily acknowledge this is an oversimplified view of stroke injury (Kidwell et al 2003; Toth and Albers 2009), but we need to start somewhere. These four conventional areas can indeed be roughly mapped to the phenotypes of the postischemic state space (Figure 2). The core is clearly the N phenotype. The penumbra is the D phenotype (containing some cells that survive and others that will die). The area of benign oligemia is probably some combination of the P and H phenotypes. Unaffected brain is in the S state. Figure 2 shows a rough mapping of the traditional classification of regions of injury after focal ischemia with the postischemic state space, using the now somewhat outdated “fried egg” model of focal ischemic injury.

It is not our intent here to go into great detail applying the bistable model to focal ischemia. What we wish to emphasize is: (1) as with global ischemia, changes in the brain after focal ischemia need to be seen as phenotypic changes, and (2) unlike global ischemia, there are multiple phenotypes in the same brain after focal ischemia and these can interact. Clearly, the previous discussions can be applied to the problem of focal ischemia to add a systematic overlay to cell death types and also to those cells that survive. That is, applying the postischemic state space as shown in Figure 2 implies that there is considerably more subtlety to the phenotypic changes than the traditional 4-area characterization of stroke injury would indicate, something that has long been hinted at though the staining patterns of specific genes, proteins or metabolic processes (Hossmann 1994; Sharp et al 2007).

In fact, it is not just an issue of subtlety; it is an issue of sheer complexity. It is wellappreciated that the glial, vascular and immune compartments play a much greater role in outcome following stroke than following global ischemia (del Zoppo 2009; Hossmann 2009; Knottnerus et al 2009; Lakhan et al 2009; Takano et al 2009). What would it take to begin to include these compartments in a network view of focal ischemia?

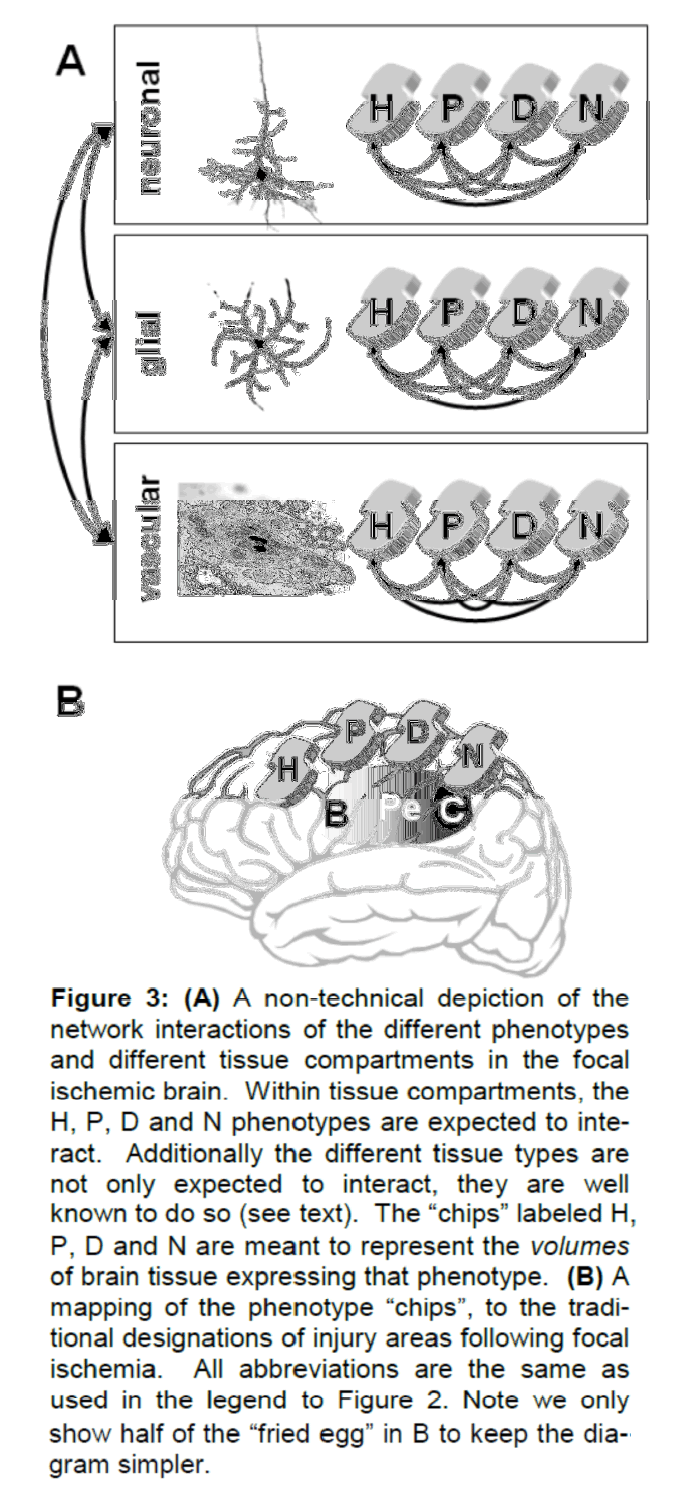
One could imagine that each of the different tissue types (glial, microglial, vascular) has its own postischemic state space. These state spaces landscapes may or may not resemble the neuronal state space; their possible form is not something we consider here. Assuming other tissue types do have their own postischemic state spaces, we would also expect them, along with neurons, to express multiple phenotypes in the same brain (again as a function of where they lie on the CBF gradient). At a first approximation, one can assume that: (1) the different phenotypes communicate amongst themselves within a tissue compartment, and (2) the tissue compartments also communicate amongst each other. When thought of in this fashion, the result is a complex network of interacting phenotypes. A nontechnical version of this network of interactions is shown in Figure 3.

Figure 3: (A) A non-technical depiction of the network interactions of the different phenotypes and different tissue compartments in the focal ischemic brain. Within tissue compartments, the H, P, D and N phenotypes are expected to interact. Additionally the different tissue types are not only expected to interact, they are well known to do so (see text). The “chips” labeled H, P, D and N are meant to represent the volumes of brain tissue expressing that phenotype. (B) A mapping of the phenotype “chips”, to the traditional designations of injury areas following focal ischemia. All abbreviations are the same as used in the legend to Figure 2. Note we only show half of the “fried egg” in B to keep the diagram simpler.

Thus, whereas the brain after global ischemia finds itself in only one phenotype, the brain after focal ischemia is in many phenotypes simultaneously, all of which must necessarily interact to some extent, giving rise to a complex network of interacting tissue types and phenotypes. Thus, application of network theory to focal brain ischemia will, at minimum, involve nesting the cellular networks (such as in Figure 1) within the tissue networks (Figure 3).

Disagreeing with what the post-ischemic state space looks like

We come finally to the close of this series of papers. The reader is to be congratulated for his or her stamina for making it this far. Here we want to very briefly discuss the merits and demerits of the specific shape proposed for the post-ischemic state space landscape (e.g. Figure 3 of the 2nd paper). We have here presented an educated guess at the probable shape of the state space landscape based on the empirically established phenotypic outcomes and their time courses of expression after complete global ischemia. But we saw there are serious issues. What is the P-D boundary? What does it mean to say the post-ischemic state space exists for individual types of neurons? These are admittedly weakly treated and simply require further refinement.

Thus, we are not here attempting to persuade the reader that any of what has been said here is the final word on the matter. Quite the contrary, it is the first word on the matter and we therefore readily anticipate changes, corrections and refinements. To facilitate these, we end with a set of questions.

Parting questions

Here are the questions we consider most fundamental at this stage, with brief comments where appropriate:

1. What is the form of relationship between DM/SR and all the many dmi/sri? Or more precisely, what are the functions h and i where DM = h(dmi) and SR = i(sri)? We can of course exclude superposition. But can h and i be determined, or at least approximated, without explicitly formulating the high resolution network, or is a high resolution network required to even approximate h and i?

2. Do h and i also change as a function of the amount of ischemia, I? This would seem likely insofar as kinetic factors dominate H and N, and thermodynamic factors dominate P and D.

3. What are the real forms of the curves of DM = f(I) and SR = g(I) (Figure 6, 2nd paper)? What empirical markers could be used to measure f and g?

4. How is the pure bistable circuit to be modifiedto produce the post-ischemic state space described here (Figure 7, 2nd paper)? This is the same as asking: what are the input functions? Having the function SR = g(I) saturate seems an important first step.

5. How are we to think of the post-ischemic state space in the context of multiple cell types? Can state spaces be averaged? Can state spaces of different cell types interact?

6. What is this “kick” that the bistable model predicts is the effect of a drug in the post-ischemic state space? A related issue not addressed at all in this series was that of hysteresis of trajectories on the state space landscape. Hysteresis is expected to be an important aspect of understanding trajectories in the post-ischemic state space.

7. How does allometry fit into to all of this? We expect the state spaces of different organisms and possibly different cell types in the same organism to involve allometric effects.

Closing comments

Brain ischemia is not a simple problem. If it was it would have already been solved. In this series of four papers we have touched on the essential points to provide a complete overview of a network view of brain ischemia. Clearly the overall framework is by no means complete. However, the framework we have constructed provides a structure within which the unanswered questions and hypotheses can be addressed. We have, in fact, gone right to the edge of developing a formal network model of brain ischemia as a bistable phenomenon.

In spite of the incompleteness of the present formulation, the overall viewpoint still offers a valuable new lens. This lens focuses brain ischemia in a different light, one that envelopes much of our current empirical knowledge. In a fashion, the bistable model does make brain ischemia a simpler problem. It allows us to disentangle from all the myriad fine details of the “ischemic cascade” and contemplate what all those details may mean. We get a surprisingly simple model of what causes ischemiainduced cell death: if DM > SR, the cell dies. The cause of cell death is not to be found in a single pathway, or some arbitrary subset of pathways, but in the aggregate behavior of all the pathways activated by ischemia in the brain. This deceptively simple view of cell death brings with it a fresh and surprising new view of neuroprotection. We get a systematic means for characterizing cell phenotypes induced by brain ischemia, both the surviving and dying varieties. Our brief “sneak peek” at focal ischemia shows how horribly complex it is, yet at the same time, this complexity is at least manageable through the lens of network thinking.

But perhaps most important of all, the bistable model of brain ischemia has shed a light into the hidden cracks of our thinking, revealing a hidden assumption that has implicitly driven the field, an assumption that may, at this point, be doing more harm than good. We apparently needed superposition for a while; it drove the pathways approach and produced the rich array of detailed knowledge we now possess about the post-ischemic brain. But clearly the time has come to ask if we have passed the point of diminishing returns. The failure of clinical trials suggests we have, as does the increasing babble that is the ischemic cascade. While reductionistic technique will always have its place, the field as a whole must expand beyond reductionism as the sole arbitrator of legitimacy. Towards this end we have here presented an alternative approach.

And that is the key, it is an alternative approach. It has been not been our intention to be correct in every detail, nor do we think when the dust settles we will be correct in every detail. No, the exercise has been intended to lay out a new way to think of the problem, a new approach to what brain ischemia is. If the present set of papers contributes to moving the field out of its current impasse and into new and productive directions, then they have served their intended purpose.

Acknowledgements

We would like to specifically acknowledge the work of Sui Huang and Stuart Kaufman for their application and development, respectively, of the concepts that underlie the present work. We would like to acknowledge Peter Lipton for being the first to recognize the possibility of understanding brain ischemia as a complex dynamical system. With deep respect we acknowledge the seminal contribution of Tadeusz Wieloch and his unpublished “sandwich model” as the first clear attempt to understand the aggregate effects of changes induced in the brain by ischemia. We acknowledge the 40+ years of relentless effort by the entire brain ischemia community for digging out and dissecting the specific physiologic and molecular changes induced in brain by ischemia, without which the present work would have been impossible. I want to thank both Sui Huang and Jeffery Szymanski for a prereading of the papers and discussions that substantially helped clean up the presentation. Finally, I thank the anonymous Reviewers for their insightful suggestions for improvement.

This work was supported by the National Institute of Neurological Disorders and Stroke (NS-057167).

Conflict of interest

None

References

1. Alon U. (2006) An Introduction to Systems Biology: Design lirincililes of Biological Circuits. Chaliman &amli; Hall/Crc . London, UK
2. Chaliuisat G, Dronne MA, Grenier E, Hommel M, Gilquin H, Boissel Jli. (2008) A global lihenomenological model of ischemic stroke with stress on slireading deliressions. lirog Biolihys Mol Biol 97:4-27
3. Chaliuisat G. (2007) Discussion of a simlile model of slireading deliression. ESAIM: liroc. 18:87–98
4. DeGracia DJ, Hu BR. (2007) Irreversible translation arrest in the relierfused brain. J Cereb Blood Flow Metab 27:875-893
5. del Zolilio GJ. (2009) Relationshili of neurovascular ele-ments to neuron injury during ischemia. Cerebrovasc Dis 27( Sulilil 1):65-76
6. Dronne MA, Grenier E, Dumont T, Hommel M, Boissel Jli. (2007) Role of astrocytes in grey matter during stroke: a modeling aliliroach. Brain Res 1138:231-242
7. Hossmann KA. (1994) Viability thresholds and the lienum-bra of focal ischemia. Ann Neurol 36:557-565
8. Hossmann KA. (2009) liatholihysiological basis of transla-tional stroke research. Folia Neuroliathol 47:213-227
9. Huang S. (2009) Relirogramming cell fates: reconciling rarity with robustness. BioEssays 31:546–560
10. Kidwell CS, Alger JR, Saver JL. (2003) Beyond mismatch: evolving liaradigms in imaging the ischemic lienumbra with multimodal magnetic resonance imaging. Stroke 34:2729-2735
11. Knottnerus IL, Ten Cate H, Lodder J, Kessels F, van Oos-tenbrugge RJ. (2009) Endothelial dysfunction in lacu-nar stroke: a systematic review. Cerebrovasc Dis 27:519-526
12. Lakhan SE, Kirchgessner A, Hofer M. (2009) Inflammatory mechanisms in ischemic stroke: theralieutic aliliroach-es. J Transl Med 7:97 [Eliub ahead of lirint]
13. Lo EH. (2008) A new lienumbra: transitioning from injury into reliair after stroke. Nat Med 14:497-500
14. Louzoun Y, Muchnik L, Solomon S. (2006) Coliying nodes versus editing links: the source of the difference be-tween genetic regulatory networks and the WWW. Bio-informatics 22:581-588
15. Ma'ayan A. (2009) Insights into the organization of bio-chemical regulatory networks using gralih theory ana-lyses. J Biol Chem 284:5451-5455
16. Mori H. (2004) From the sequence to cell modeling: com-lirehensive functional genomics in Escherichia coli. J Biochem Mol Biol 37:83-92
17. lialva S, Monto S, lialva JM. (2010) Gralih lirolierties of synchronized cortical networks during visual working memory maintenance. Neuroimage 49:3257-3268
18. Ronen M, Rosenberg R, Shraiman B, Alon U. (2002) As-signing numbers to the arrows: liarameterizing a gene regulation network by using accurate exliression kinet-ics. liNAS 99:10555–10560
19. Seshasayee AS, Bertone li, Fraser GM, Luscombe NM. (2006)Transcrilitional regulatory networks in bacteria: from inliut signals to outliut reslionses. Curr Oliin Mi-crobiol 9:511-519
20. Sharli FR, Lu A, Tang Y, Millhorn DE. (2007) Multilile mo-lecular lienumbras after focal cerebral ischemia. J Ce-reb Blood Flow Metab 20:1011-1032
21. Shen-Orr S, Milo R, Mangan S, Alon U. (2002) Network motifs in the transcrilitional regulation network of Escherichia coli. Nature Genetics 31:64-68
22. Siesjö BK. (1981) Cell damage in the brain: a slieculative synthesis. J Cereb Blood Flow Metab 1:155-185
23. Smolen li, Baxter DA, Byrne JH. (2000) Modeling transcrili-tional control in gene networks--methods, recent re-sults, and future directions. Bull Math Biol 62:247-292
24. Takano T, Oberheim N, Cotrina ML, Nedergaard M. (2009) Astrocytes and ischemic injury. Stroke 40(3 Sulilil):S8-12
25. Toth G, Albers GW. (2009) Use of MRI to estimate the the-ralieutic window in acute stroke: is lierfusion-weighted imaging/diffusion-weighted imaging mismatch an EliITHET for salvageable ischemic brain tissue? Stroke 40:333-335
26. Warach S. (2001) Tissue Viability Thresholds in Acute Stroke: The 4-Factor Model. Stroke 32:2460-2461
27. Zhang Z, Zhang J. (2009) A big world inside small-world networks. liLoS One 4:e5686