Steady-state MRI: methods for neuroimaging

¹FMRIB Centre, University of Oxford, Oxford, UK

²Montreal Neurological Institute, Montreal, Canada

Corresponding Author:

Karla L Miller
Author for correspondence: FMRIB Centre
John Radcliffe Hospital, Oxford, OX3 9DU, UK
Tel: +44 186 522 2551
E-mail: karla@fmrib.ox.ac.uk

Abstract

MRI pulse sequences that use regularly spaced trains of rapidly applied excitation pulses (every few milliseconds) are known as ‘steady-state’ sequences. Under these conditions, the magnetization evolves into a steady state that depends on tissue parameters such as T1, T2 and diffusion, as well as sequence parameters such as repetition time and flip angle. These sequences have attractive properties including high efficiency (in terms of signal-to-noise ratio) and flexible image contrast; they also create unique challenges due to the need to maintain the magnetization in the steady state and their complicated signal dependence. This article describes the primary types of steady-state sequences and their application to brain imaging.

Keywords

angiography ▪ brain ▪ diffusion ▪ flow ▪ fMRI ▪ MRI ▪ neuroimaging ▪ SSFP ▪ steady-state ▪ susceptibility

Steady-state imaging

What is steady-state imaging?

In the context of MRI pulse sequences, the term ‘steady state’ typically refers to the equilibrium condition that evolves when magnetization experiences a train of radiofrequency (RF) pulses. If RF pulses occur at broadly spaced intervals (repetition time [TR] > T₁), the magnetization recovers fully between pulses due to relaxation, and the steady-state is identical to the fully relaxed magnetization, M0. However, in general, RF pulses are applied sufficiently rapidly that the magnetization does not recover fully between pulses (TR < T₁), and the magnetization eventually develops a steady-state condition that is distinct from M0. In this manuscript, we assume that both TR and flip angle (a) are constant throughout the pulse sequence.

For most MRI pulse sequences, TR is on the order of seconds, making it of similar magnitude to T₁, but much longer than T₂. In this case, at the end of the TR, the magnetization has decayed away completely in the transverse plane, but has not yet recovered fully along the longitudinal axis. The result is a ‘longitudinal steady state’, where the magnetization tipped away from the longitudinal axis by an RF pulse is exactly cancelled by recovery of magnetization along the longitudinal axis during the TR. Longitudinal steady states depend on the T₁ of tissue, but not T₂.

However, ‘steady-state sequences’ commonly refer to a more specific case in which both T₁ and T₂ relaxation are interrupted by very rapid RF pulses (TR ≤ T₂ < T₁). In this situation, there is residual transverse magnetization at the end of the TR, which experiences the subsequent RF pulse. We would describe the result as a ‘transverse steady state’ (with the understanding that this necessarily implies steady state of the longitudinal component, as well). Again, we can determine the steady state by imposing the equilibrium condition that the effects of relaxation and precession of the magnetization during the TR must be exactly cancelled by the RF pulse.

The signal dynamics of steady-state sequences are considerably more complicated than conventional sequences, and depend on T₁, T₂ and the phase (angle) between the magnetization and the axis of the RF pulse. In fact, it is the dependence of the steady state on phase that leads to the tremendous richness and flexibility of steady-state sequences, as well as many of the complications in dealing with these methods.

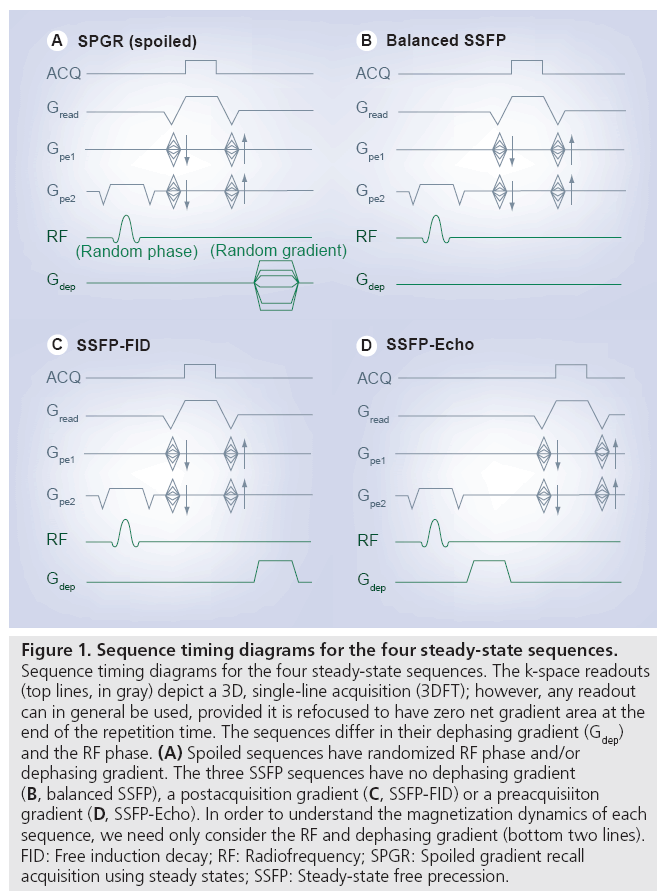
Steady-state sequences differ based on how the transverse magnetization is manipulated to influence contrast, and can be considered to fall into three categories: spoiled gradient echo, balanced steady-state free precession (SSFP) and unbalanced SSFP. Unfortunately, nomenclature is not standardized, and these sequences are also known by the names given in Table 1. Timing diagrams for the sequences discussed here are depicted in Figure 1.

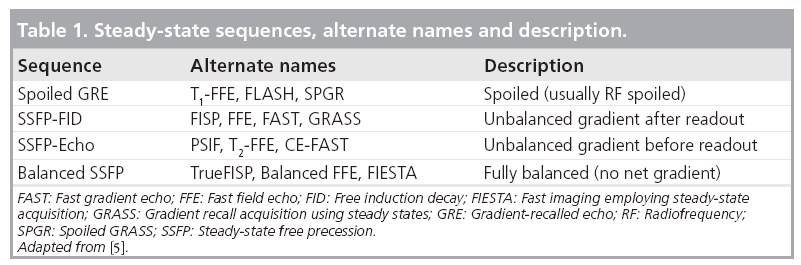
Figure 1: Sequence timing diagrams for the four steady-state sequences. Sequence timing diagrams for the four steady-state sequences. The k-space readouts (top lines, in gray) depict a 3D, single-line acquisition (3DFT); however, any readout can in general be used, provided it is refocused to have zero net gradient area at the end of the repetition time. The sequences differ in their dephasing gradient (Gdep) and the RF phase. (A) Spoiled sequences have randomized RF phase and/or dephasing gradient. The three SSFP sequences have no dephasing gradient (B, balanced SSFP), a postacquisition gradient (C, SSFP-FID) or a preacquisiiton gradient (D, SSFP-Echo). In order to understand the magnetization dynamics of each sequence, we need only consider the RF and dephasing gradient (bottom two lines). FID: Free induction decay; RF: Radiofrequency; SPGR: Spoiled gradient recall acquisition using steady states; SSFP: Steady-state free precession.

Spoiled sequences

Spoiling aims to manipulate the residual magnetization that remains at the end of the TR such that it does not contribute signal in subsequent repetition periods. If this can be achieved, the signal will be a fairly pure T₁ contrast [1], although the signal level will by definition be reduced compared with unspoiled sequences that do not attempt to remove the residual transverse signal. Spoiled sequences are typically used when the primary goal of using short TR is acquisition speed, rather than to exploit steady-state signal dynamics to achieve novel contrast.

Gradient spoiling

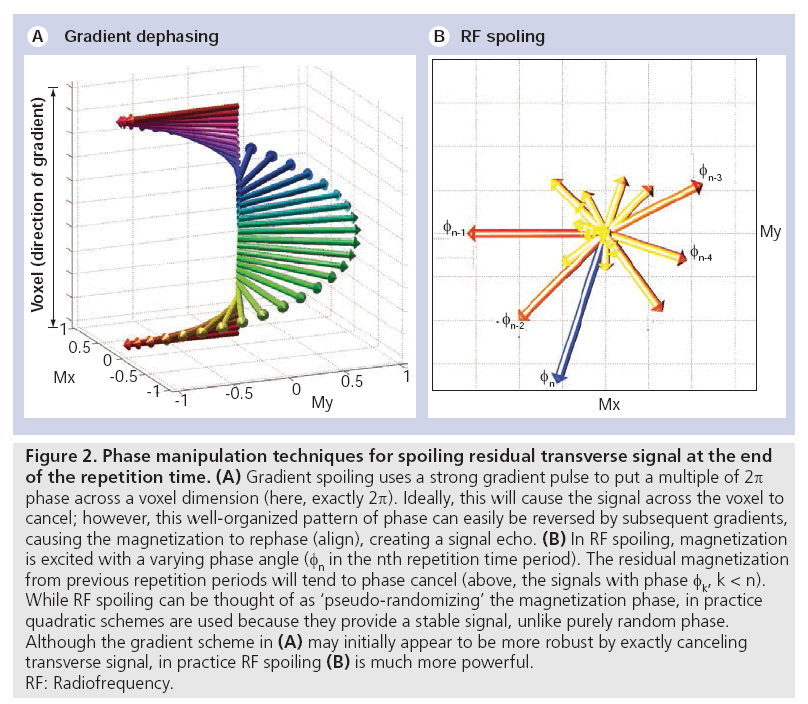
The easiest spoiling method to understand is gradient spoiling, in which a gradient pulse is used to create a range of phase angles across a voxel. This ‘dephasing’ effect causes the transverse magnetization to self-cancel (Figure 2A). However, these gradients have not destroyed the transverse magnetization, but simply suppressed its signal. If the same spoiling gradient is used every TR, a fraction of the dephased magnetization will be rephased to form a signal echo in later TRs (in fact, the use of a fixed gradient would make this an ‘unbalanced SSFP’ sequence, described below). Proper gradient spoiling requires a randomized gradient each TR to avoid this rephasing. However, achieving a broad range of variable areas requires either very strong gradients or long TR, making this impractical under most circumstances. In addition, the quality of spoiling is spatially dependent, with no spoiling at the center of the gradients [2]. These limitations make RF spoiling the preferred technique.

Figure 2: Phase manipulation techniques for spoiling residual transverse signal at the end of the repetition time. (A) Gradient spoiling uses a strong gradient pulse to put a multiple of 2p phase across a voxel dimension (here, exactly 2p). Ideally, this will cause the signal across the voxel to cancel; however, this well-organized pattern of phase can easily be reversed by subsequent gradients, causing the magnetization to rephase (align), creating a signal echo. (B) In RF spoiling, magnetization is excited with a varying phase angle (fn in the nth repetition time period). The residual magnetization from previous repetition periods will tend to phase cancel (above, the signals with phase fk, k < n). While RF spoiling can be thought of as ‘pseudo-randomizing’ the magnetization phase, in practice quadratic schemes are used because they provide a stable signal, unlike purely random phase. Although the gradient scheme in (A) may initially appear to be more robust by exactly canceling transverse signal, in practice RF spoiling (B) is much more powerful.
RF: Radiofrequency.

RF spoiling

A more powerful technique for removing the signal contribution from residual transverse magnetization is RF spoiling. The basic idea is to tip the magnetization about a different axis in each TR [3]. The transverse magnetization that is excited in one TR will therefore have a phase angle that is offset relative to the magnetization that persists from prior excitations. If the tip axes are chosen appropriately, fresh signal from the most recent RF pulse will dominate, while residual transverse components will phase cancel (another form of dephasing [Figure 2B]). RF spoiling is often described as ‘pseudo-randomizing’ the phase of the RF pulse, but in fact random phase angles can lead to signal instability [4]. In practice, a quadratic schedule of phase angles has been shown to provide a stable signal [4]. In quadratic phase cycling, the phase for the nth RF pulse is given by Φ_n=n(n+1)ΔΦ and constant increment, ΔΦ. The effectiveness of RF spoiling in creating pure T₁ contrast is critically dependent on the specific phase increment. Suppression of residual transverse magnetization makes the signal approximately independent of T₂, resulting in a signal that is a relatively pure T₁ contrast. A helpful discussion of RF spoiling is given in [5].

Steady-state free precession

Unlike spoiled sequences, SSFP techniques aim to make use of the residual transverse magnetization at the end of each TR period. These sequences have fixed dephasing gradients and constant (or, in some cases, linearly increasing) RF phase [6]. In order to be in the steady state, the magnetization vector must behave identically from one TR to the next. For this constraint to be satisfied, the RF pulse must exactly cancel all sources of motion that the magnetization vector experiences during the TR, thus placing the magnetization vector back where it started [3]. Sources of motion of the magnetization vector include relaxation (reorienting the vector relative to the transverse plane) and precession (rotating the vector about the longitudinal axis). The T₁, T₂, flip angle and phase angle (due to off-resonance or gradient-induced precession) exactly determine the magnetization vector that satisfies this steady-state condition. Unlike most sequences, in which magnetization dynamics are dominated by relaxation, precession is the dominant effect in SSFP. Balanced and unbalanced SSFP sequences differ in the source of this phase accrual, and in the way signal sums across a voxel.

Balanced SSFP

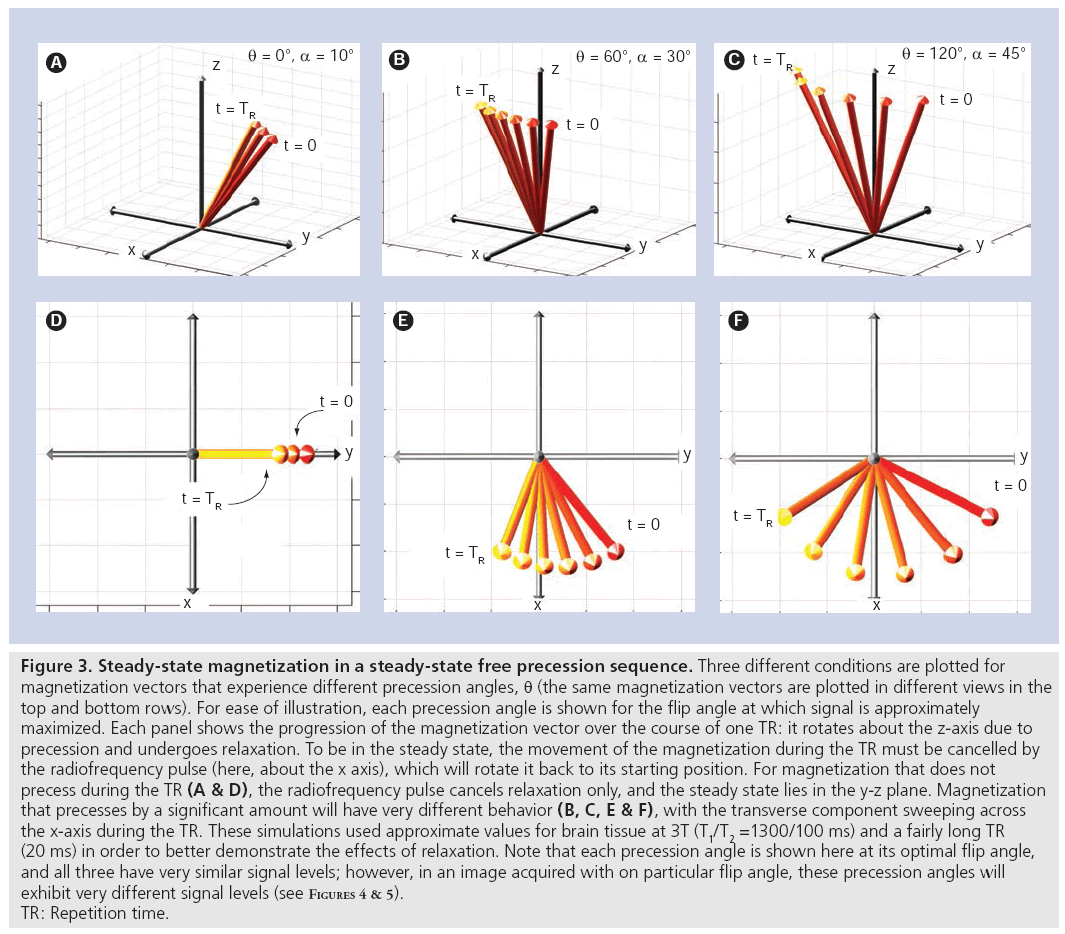
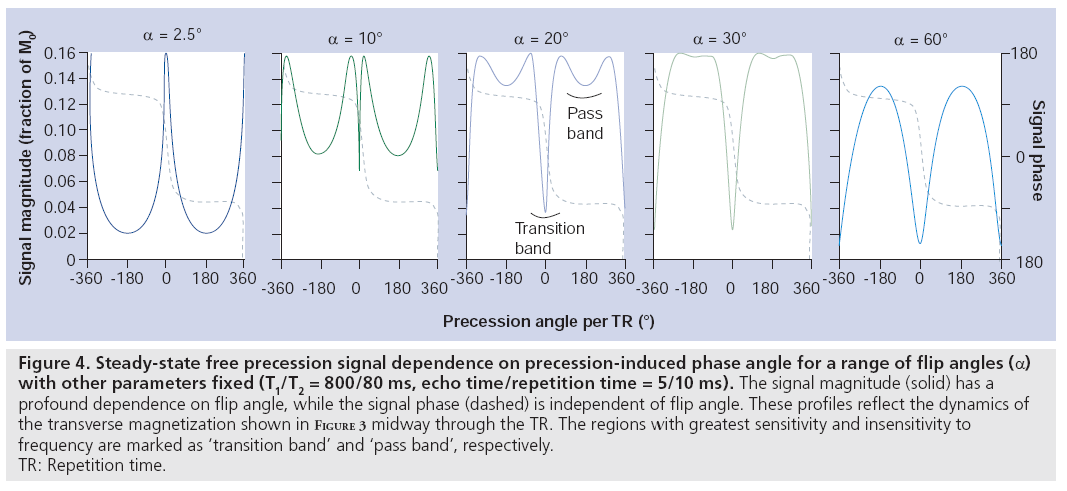
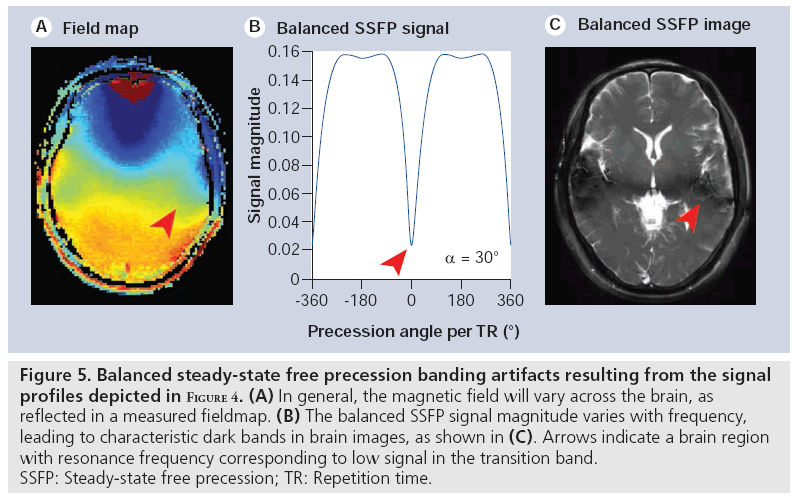
Balanced SSFP has the key characteristic that all gradients are fully refocused (have zero net area) across a repetition period [7]. The only source of phase accrual during the TR is therefore due to off-resonance precession (e.g., precession due to field variations reflecting an imperfect shim). To be in the steady state, rotation due to precession must be cancelled by the RF tip, which causes the steady-state magnetization vectors for different resonance frequencies to differ (see examples in Figure 3). The well-shimmed voxels in typical MRI experiments will be roughly characterized by a single resonance frequency. The intriguing result is that the voxel signal depends on its resonance frequency (Figure 4), creating image contrast that reflects the local magnetic field in addition to T₁ and T₂ [8]. Although individual voxels are typically well shimmed, the frequency will slowly vary across the brain, creating lowsignal regions (‘banding artefacts’), as depicted in Figure 5. These bands are often considered artefacts in balanced SSFP imaging, but can also be used as a source of contrast, as described below. The SSFP signal profile shown in Figure 4 can be divided into two regions: the transition band, where signal is exquisitely sensitive to small changes in resonance frequency, and the pass band, where it is relatively insensitive to frequency. Since the frequency dependence of the signal is driven by the amount of precession- induced rotation between RF pulses, the distance between transition bands is dependent on the time between pulses, the TR. As the TR changes, the bands remain TR-1 Hz apart. The balanced SSFP signal does nevertheless depend on relaxation, and is often stated to have T₂/ T₁ contrast (provided imaging occurs in the passband with TR<<T₂ and at the optimal flip angle [9]). In the brain, this ratio yields almost no contrast between gray and white matter. Neuroimaging with balanced SSFP therefore tends to either focus on alternative contrast mechanisms (e.g., diffusion or flow) or differential contrast to separate the effects of T₁ and T₂ (e.g., quantitation or functional MRI [fMRI]). Finally, there is also a fairly complicated dependence of the signal on flip angle (Figure 4), a full discussion of which is outside of the scope of this article.

Figure 3: Steady-state magnetization in a steady-state free precession sequence. Three different conditions are plotted for magnetization vectors that experience different precession angles, q (the same magnetization vectors are plotted in different views in the top and bottom rows). For ease of illustration, each precession angle is shown for the flip angle at which signal is approximately maximized. Each panel shows the progression of the magnetization vector over the course of one TR: it rotates about the z-axis due to precession and undergoes relaxation. To be in the steady state, the movement of the magnetization during the TR must be cancelled by the radiofrequency pulse (here, about the x axis), which will rotate it back to its starting position. For magnetization that does not precess during the TR (A & D), the radiofrequency pulse cancels relaxation only, and the steady state lies in the y-z plane. Magnetization that precesses by a significant amount will have very different behavior (B, C, E & F), with the transverse component sweeping across the x-axis during the TR. These simulations used approximate values for brain tissue at 3T (T₁/T₂ =1300/100 ms) and a fairly long TR (20 ms) in order to better demonstrate the effects of relaxation. Note that each precession angle is shown here at its optimal flip angle, and all three have very similar signal levels; however, in an image acquired with on particular flip angle, these precession angles will exhibit very different signal levels (see Figures 4 & 5).
TR: Repetition time.

Figure 4: Steady-state free precession signal dependence on precession-induced phase angle for a range of flip angles (a) with other parameters fixed (T₁/T₂ = 800/80 ms, echo time/repetition time = 5/10 ms). The signal magnitude (solid) has a profound dependence on flip angle, while the signal phase (dashed) is independent of flip angle. These profiles reflect the dynamics of the transverse magnetization shown in Figure 3 midway through the TR. The regions with greatest sensitivity and insensitivity to frequency are marked as ‘transition band’ and ‘pass band’, respectively. TR: Repetition time.

Figure 5: Balanced steady-state free precession banding artifacts resulting from the signal profiles depicted in Figure 4. (A) In general, the magnetic field will vary across the brain, as reflected in a measured fieldmap. (B) The balanced SSFP signal magnitude varies with frequency, leading to characteristic dark bands in brain images, as shown in (C). Arrows indicate a brain region with resonance frequency corresponding to low signal in the transition band. SSFP: Steady-state free precession; TR: Repetition time.

Unbalanced SSFP

A second type of SSFP sequence includes an unbalanced gradient pulse [10]. At first glance, the unbalanced sequence in Figure 1C bears a strong resemblance to the gradient-spoiled sequence in Figure 1A. The crucial difference is that the gradient ‘spoiler’ in unbalanced SSFP does not vary from one TR to the next. The effects of the gradient pulse during one repetition period can be reversed to reform the signal in subsequent TRs (the details of this signal formation are nicely described in [11]). In terms of signal dynamics, unbalanced SSFP is actually very closely related to balanced SSFP, since the magnetization steady state is determined by net precession during the TR. This phase is constant across a voxel in balanced SSFP, whereas in unbalanced SSFP, this phase angle varies within the voxel. The detected signal in unbalanced SSFP is the summation of the signal across the voxel (i.e., the average of the transverse magnetization shown in Figure 4). The resulting images therefore do not exhibit banding. The final characteristic that affects unbalanced SSFP sequences is whether the gradient occurs before or after the readout. If the gradient occurs after the readout, magnetization that is freshly excited by the RF pulse, the free induction decay (FID), contributes signal, giving rise to one name for this sequence: SSFP-FID. If the gradient occurs before the readout, fresh magnetization is immediately dephased and does not contribute signal, such that all signal comes from ‘echoes’ formed over multiple TRs, and the sequence is an SSFP-Echo.

Properties of steady-state imaging

Steady-state sequences span a broad range of imaging strategies and signal mechanisms; however, there are a number of properties of steadystate sequences that differ from more ‘conventional’ sequences. In this section, we describe a few key properties common to steady-state sequences.

Maintaining the steady state

One key property of steady-state sequences, which is often invisible to the end user but nevertheless dictates many of the decisions and techniques employed, is the need to achieve and maintain the steady state. The steady state is only established after RF pulses are applied for a duration of approximately 3 × T₁, during which time the signal can be highly unstable. Many techniques that form a part of the conventional MRI sequence toolkit are considerably more difficult to achieve while maintaining the steady state. For example, conventional methods for fat saturation, inversion recovery and flow sensitization would disturb the steady state, necessitating different approaches. One important discovery in steady-state imaging is the ability to ‘catalyze’ the steady state: to apply a series of RF pulses that places the magnetization close to its final steady state [12,13]. Catalyzation reduces transient signal oscillations, thereby enabling acquisition to commence immediately rather than waiting for the steady state to develop [14].

3D acquisition

In order to maintain the transverse steady state, we must satisfy the condition that TR ≤ T₂, which in general means TR < 50–100 ms. The use of 2D multislice excitations in this range of TR would require us to image slice-byslice, re-establishing the steady state for each slice in turn, sacrificing the signal-to-noise ratio (SNR) efficiency advantage. Therefore, steady-state sequences almost always utilize 3D, slab-selective k-space acquisitions, acquiring a small subset of 3D k-space each TR. These acquisitions are highly SNR efficient and tend to have low image distortion. However, they are also sensitive to certain sources of artefact, such as motion and flow, and preclude some options such as interslice gaps. Several groups have proposed flow- and motion-compensation schemes for cardiac imaging (e.g., [15,16]), but these methods remain largely unexplored in the brain.

Low flip angle

Conventional sequences with long TR often use 90° excitation pulses to maximize signal. However, for short TR, signal can actually increase at lower flip angle (with the optimum often referred to as the ‘Ernst angle’). This is particularly true for the range of TR used in steady-state sequences, where the maximum signal is often achieved with f lip angles of 30–40°. In addition, many of the steady-state techniques described below (e.g., fMRI and diffusion imaging) achieve optimal contrast (as distinct from optimal signal) at much lower flip angles of 5–30°. One consequence of this is that steady-state methods often have low RF energy deposition, even though RF pulses may be applied rapidly. However, the use of TR on the order of 2–5 ms does mean that flip angles as low as 60° can be constrained by energy deposition, even at 3T.

High SNR efficiency

The key property defining steady-state sequences is the use of very short TR, and these sequences are often described as ‘rapid imaging’. In practice, steady-state sequences do not necessarily have short acquisition times (i.e., 3D image formation can take minutes), but they are characterized by very efficient acquisitions [17]. This property arises due to the similar timescale of the TR and typical k-space readouts: milliseconds to tens of milliseconds. Most steady-state sequences therefore allow the majority of the TR to be dedicated to acquiring data. This allows steadystate sequences to overcome the very low intrinsic signal levels caused by short TR. Although the baseline signal that is acquired can be as low as 5–15% of M0, the efficiency of the readout (occupying 60–90% of the TR) will often more than make up for this in the final SNR of the image. The SNR efficiency of spoiled steadystate sequences is considerably lower, despite similar TRs. These sequences do not reuse the transverse magnetization over multiple TR periods and therefore have drastically reduced baseline signal (up to five-times less signal than SSFP sequences).

Complicated signal dependence

One of the biggest challenges with steady-state sequences is that increased efficiency comes at the cost of a more complicated signal. As mentioned above, the signal in steady-state sequences is in general sensitive to T₁, T₂ and phase accrual. With the proper tools for understanding this behavior, this complexity can lead to a fascinating degree of flexibility and interesting signal behavior. However, this complicated dependence is also a critical confound to unambiguously interpreting the signal in steady-state images. As will be seen below, a common theme in quantification with steady-state sequences is the difficulty in designing methods that are able to isolate one parameter of interest (e.g., relaxation and magnetization transfer) while controlling for other signal dependences.

Neuroimaging applications of steady-state sequences

The broad range of contrast mechanisms, quantification techniques and imaging strategies that have been proposed using steady-state sequences is far too extensive to be treated exhaustively here. Below, we focus on the techniques (and literature) that are most relevant to brain imaging, and those that rely critically on the unique strengths of steady-state imaging. The examples discussed below are chosen to highlight the common themes of contrast mechanisms, as well as the shortcomings and confounds that underpin steady-state neuroimaging. However, this is not intended as a comprehensive literature review, and many relevant references have of necessity been omitted.

Quantitative measures: T₁, T₂ & MT

There are several MR properties of tissue that would be useful to quantify in the brain, with the most prominent being T₁, T₂ and magnetization transfer (MT). These properties have been linked to aspects of brain tissue microstructure, such as myelin content [18–20]. These quantities have also been shown to alter under neuropathological conditions. Steady-state sequences are compelling for quantifying these properties, since most conventional quantitative techniques tend to be time-consuming and the steady-state alternatives are considerably faster. However, the sensitivity of steady-state techniques to such a broad range of tissue properties can make quantification difficult.

T₁ mapping

Steady-state imaging methods have great potential to achieve rapid T₁ mapping in the brain. The most widespread method involves acquiring multiple spoiled-GRE images at varying flip angle, which alters the amount of T₁ weighting, enabling T₁ to be fit in each voxel [21]. This method is known by several names, including variable flip (nutation) angle [22], limited flip angle [23] and DESPOT [24]. At high field strengths (3T and above), RF inhomogeneities cause the achieved flip angle to vary across the brain. Several groups have proposed the acquisition of additional scans to estimate flip angle maps for use in T₁ fitting [25–27]. Another possibility is to acquire steady-state images following an inversion preparation using a spoiled [28] or balanced SSFP [29] readout. Since these readouts continually excite the magnetization recovery, fresh magnetization is mixed in and must be accounted for.

MT mapping

In MT imaging, off-resonance saturation pulses are typically used to saturate protons that are bound to macromolecules, such as those found in myelin [30,31]. While the vast majority of MT imaging is nonquantitative (mapping the MT ratio), several groups have suggested quantitative techniques using MT-prepared, spoiled-GRE sequences to estimate the size of this pool and the rate of exchange between water and macromolecular protons [32–34]. These methods rely on combining T₁ mapping with multiple MT measurements and a two-pool model [35]; however, they are time-consuming and RF intensive. Alternatively, SSFP can shorten the acquisition time by taking advantage of the intrinsic on-resonance MT effects of excitation pulses, eliminating the need for long MT preparations [36]. Balanced [37] and unbalanced [38] SSFP sequences have been used to provide rapid 3D maps of MT parameters.

T₂ mapping

Several groups have proposed methods for quantifying T₂ using balanced SSFP methods. Since the signal depends on both T₁ and T₂, these methods also require an estimate of T₁. One method, DESPOT₁/2, extends the variable flip angle approach to acquire both spoiled-GRE and balanced SSFP images at several flip angles to estimate T₁ and T₂ [39]. The inversion–recovery balanced SSFP method for T₁ mapping has also been extended to map T₁ and T₂ values [40]. One important issue for quantification methods based on balanced SSFP is the presence of banding artefacts. This can be addressed by combining multiple images with the bands shifted, which can be accomplished trivially through alterations of the RF phase [41]. The resonance frequency can then be accounted for as an additional parameter in the fitting [42]. However, as discussed below, care must also be taken to account for variable flip angle, exchange and MT effects for accurate quantification.

Challenges for quantification

The sensitivity of steady-state sequences to a broad range of tissue properties is a pervasive theme in steady-state imaging, which poses considerable challenges to quantification. For example, the sensitivity of steady-state sequences to MT is an important confound for variable flip-angle acquisitions, since the sensitivity to MT will also in general vary with flip angle [43]. Similarly, water diffusion [44] and exchange [45,46] during balanced SSFP sequences causes the apparent T₂ to vary with TR. Systematic variations, including B0 [42], flip angle [25–27] and finite RF pulses [46,47], also must be taken into account. These issues directly impact the biological interpretation of tissue parameters, such as myelin quantification using two-pool models [46].

Functional MRI

Functional MRI detects metabolic changes associated with brain activity based on the blood oxygen level dependent (BOLD) effect, in which the blood experiences a frequency shift when hemoglobin is stripped of oxygen [48,49]. This frequency shift leads to a more complicated pattern of frequency broadening in the extravascular tissue, which is typically detected as a change in the T₂ or T₂* relaxation of tissue. Conventional fMRI suffers from signal dropout (or ‘black holes’), image distortion and poor resolution. Several groups have proposed methods for addressing these shortcomings using SSFP sequences with a range of contrast mechanisms.

The first method proposed for fMRI using SSFP attempts to detect the BOLD frequency shift directly based on the frequency sensitivity of balanced SSFP [50,51]. This frequency shift during brain activity causes the voxel to shift along the SSFP profile in Figure 4. Provided the voxel lies in the region of greatest sensitivity to frequency (0 Hz in Figure 4), the signal magnitude will change. This method is often referred to as transition-band SSFP fMRI, since it requires the voxel to lie in the transition band. Several groups subsequently reported signal changes even for voxels in the relatively flat passband of the SSFP profile [52–54], where frequency shift should not alter signal magnitude. These signal changes have been shown to reflect T₂ BOLD changes, as observed previously in blood samples [55]. While passband SSFP signal changes can be observed even at short echo time (TE; 3–6 ms), increased signal changes at long TE likely reflect broadening of the range of frequencies in a voxel, the source of the T₂* BOLD effect [56]. fMRI signal can also be obtained with unbalanced SSFP sequences, including both SSFP-FID [53] and SSFP-Echo [57] acquisitions. This relatively complicated picture of signal changes due to frequency shift, frequency broadening and T₂ changes can be understood with a more realistic picture of SSFP signal that takes into account the full distribution of frequencies within a voxel (instead of assuming a single voxel frequency) [58,59]. This picture is consistent with the full range of SSFP signal formation mechanisms. A final technique for detecting neuronal currents directly with SSFP is, unfortunately, outside the scope of this article [60].

The primary attraction of these techniques is their potential to decouple the source of fMRI contrast from image distortion and signal dropout. This has enabled groups to demonstrate fMRI with high resolution [54,61] and near susceptibility boundaries [62,63]. In addition, SSFP has the advantage at high field of enabling T₂ contrast with low RF power deposition [57]. However, these methods also have several important shortcomings. With balanced SSFP, it is difficult to achieve whole-brain contrast in one scan due to imperfect shim, leading to variable contrast across the brain due to banding artifacts. Although it is possible to combine data from multiple scans [51], the use of multiple scans incurs a major increase in scan time. Although passband and unbalanced SSFP are less sensitive to banding, these techniques are also less sensitive to the BOLD effect of interest [58]. SSFP methods are also highly sensitive to physiological fluctuations, which cannot easily be addressed in postprocessing. Several groups have proposed to reduce this sensitivity with real-time corrections based on physiological monitoring [64–66].

Susceptibility-weighted contrast

Magnetic susceptibility is the tendency of a given material (or tissue) to become magnetized in an external magnetic field. A number of techniques take advantage of the fact that materials with shifted magnetic susceptibility cause alterations in frequency that can be detected in the MRI signal, such as the BOLD effect due to the susceptibility shift of deoxyhemoglobin. Where fMRI uses the BOLD effect to detect dynamic changes from blood vessels that are much smaller than a voxel, susceptibility-weighted imaging acquires high-resolution images to resolve veins as focal regions of low signal [67]. More recently, several groups have reported susceptibility contrast in white and gray matter [68–70] that appears to relate to other susceptibility-shifted tissue constituents, such as iron and myelin [71,72]. It is important to note that these techniques all detect susceptibility shifts relative to an explicit or implicit reference, and cannot directly calculate the total susceptibility.

Several methods for detecting susceptibility effects with SSFP have been proposed. These methods are inspired in part by SSFP fMRI methods relating signal magnitude [50] and phase [51] to frequency shifts, as well as more complicated features of the frequency distribution [50,58]. Signal magnitude changes have been used to detect frequency shifts caused by injected susceptibility agents [73] and cells labeled with susceptibility-shifted particles [74–76]. Based on observations of amplified phase changes in fMRI using SSFP [77], another group has demonstrated strong phase changes for endogenous susceptibility contrast [78]. Preliminary results combining multiple unbalanced echoes (SSFP-FID, SSFP-Echo and a third signal pathway) have shown excellent conspicuity of deep brain nuclei [79]. Finally, our group has demonstrated alterations in the balanced SSFP profile (Figure 4) that are believed to be driven by magnetic susceptibility [80]. These effects are particularly prominent in white matter [81], and have a striking similarity to contrast observed in more conventional susceptibility imaging at high field [82]. Understanding the source of this contrast is currently a topic of intense focus, and the role that steady-state techniques may have to play is far from clear.

Diffusion imaging

Diffusion imaging tracks the movement of water molecules in the presence of tissue microstructure, which hinders and restricts the natural tendency of water to diffuse freely in all directions. Diffusion can be detected with MRI by applying strong gradients to encode and then decode spatial positions at a very fine scale, typically using a spin-echo sequence [83]. This enables detection of pathological microstructure and the tracking of white matter fibers. However, the singleshot acquisitions employed to ‘freeze’ subject motion [84] incur significant image distortion and limit spatial resolution. Spin-echo sequences also couple the amount of diffusion weighting to echo time, introducing a problematic trade-off between contrast and SNR. Several steady-state imaging techniques have been proposed to deal with these issues.

One of the first methods proposed for diffusion- weighted imaging was a relatively straightforward extension of unbalanced SSFP imaging, in which the dephasing gradient is particularly strong and serves to impart diffusion weighting [85,86]. This single diffusion gradient occurs after excitation and before data acquisition (i.e., a SSFP-Echo sequence). The diffusion-weighted signal is fundamentally linked to the steady-state nature of the sequence: the encoding and decoding pairs of diffusion gradients are implicitly formed over multiple TRs, and magnetization that persists over multiple TRs becomes diffusion weighted [87]. This creates the potential for acquiring data with strong diffusion weighting at short echo time. Like most steady-state imaging methods, this sequence bears a complicated signal dependence on T₁, T₂ and flip angle, in addition to the diffusion coefficient [87,88]. The crucial problem with this method, however, is its extreme sensitivity to motion [89]. Several groups have proposed methods for reducing [90] or removing [91–93] the effects of motion, but to date this problem remains largely unsolved.

A second category of steady-state imaging methods combines the use of a steady-state readout train with a more standard (spin echo) diffusion-weighting preparation [94]. The key benefit compared with conventional diffusion imaging is that multiple readouts can be acquired for each diffusion-weighting period. However, the measured signal becomes contaminated with nondiffusion-weighted signals excited by the RF train. Various methods have been proposed to address the sensitivity of these methods to motion [95,96] and eddy currents [97].

For a more comprehensive review on steadystate diffusion imaging, see [98].

Angiography & flow imaging

The ability to visualize the anatomy and function of blood vessels is of considerable importance in cerebrovascular disease, and steadystate sequences are an attractive option for imaging flowing blood. First, fresh blood moving into the imaging region has not experienced previous RF pulses and therefore has relatively high signal intensity compared with static tissue (the ‘inflow’ effect). This is the basis of the commonly used time-of-flight technique [99], often implemented with a spoiled-GRE readout. Second, in balanced SSFP, the large T₂/ T₁ ratio of blood yields high signal relative to most other tissues, especially at higher flip angles [100]. Third, good SNR efficiency and rapid k-space coverage allow the acquisition of high-resolution images within reasonable scan times.

The conspicuity of blood vessels can be enhanced through an appropriate preparation. The injection of a contrast agent dramatically reduces the T₁ of blood, giving high signal intensities in spoiled GRE [101] and to a greater extent in balanced SSFP [9]. Noninvasive labeling methods have also been suggested, either by combining steady-state readouts with inversion preparations [102,103], or by incorporating flow contrast into the steady state [104]. Steady-state sequences lend themselves to dynamic readout strategies to obtain information regarding vessel function in addition to the morphology [101,105]. Novel methods for phase contrast imaging, in which additional gradients are used to encode blood velocity information in the phase images, have also been developed using steady-state techniques [106–108].

However, there are a number of difficulties associated with these methods. The movement of blood during the application of gradients causes additional phase accrual that can lead to artefacts such as signal dropout (although, of course, phase-contrast techniques rely on this mechanism for contrast). Balanced SSFP suffers from further complications: out-of-slice effects may be significant in 2D imaging [109] and careful ordering of phase-encoded lines or even full flow compensation may sometimes be necessary [15]. When imaging commences soon after a preparation scheme, transient oscillations can lead to significant artefacts unless an appropriate catalyzation method is used, as mentioned previously. With care to avoid these problems, several groups have produced excellent angiographic images using balanced SSFP [103,105].

Steady-state imaging methods have also been applied to a number of related areas, such as the mapping of cerebral blood flow at the tissue level (where balanced SSFP offers reduced distortion compared with conventional echo-planar imaging methods [110]) and the assessment of CSF flow [108].

Future perspective

Steady-state imaging may play a major role in the future of neuroimaging as MRI hardware continues to evolve in ways that support the demands of fast imaging and the ability to further accelerate acquisition. The primary challenges for these techniques lie in reducing the sensitivity to physiological instabilities and providing robust quantification in the face of complicated signal dependences.

Financial & competing interests disclosure

The authors have no relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript. This includes employment, consultancies, honoraria, stock ownership or options, expert testimony, grants or patents received or pending, or royalties.

No writing assistance was utilized in the production of this manuscript.

References

Papers of special note have been highlighted as:

• of interest

1. Haase A, Frahm J, Matthaei D, Hanicke W, Merboldt KD: FLASH imaging. Rapid NMR imaging using low flip-angle pulses. J. Magn. Reson. 67, 258–266 (1986).
2. Crawley AP, Wood ML, Henkelman RM: Elimination of transverse coherences in FLASH MRI. Magn. Reson. Med. 8, 248–260 (1988).
3. Freeman R, Hill HDW: Phase and intensity anomalies in fourier transform NMR. J. Magn. Reson. 4, 366–383 (1971).
4. Zur Y, Wood ML, Neuringer LJ: Spoiling of transverse magnetization in steady-state sequences. Magn. Reson. Med. 21, 251–263 (1991).
5. Bernstein MA, King KF, Zhou XJ: Handbook of MRI Pulse Sequences. Elsevier Academic Press, Burlington, MA, USA (2004).
6. Zur Y, Stokar S, Bendel P: An analysis of fast imaging sequences with steady-state transverse magnetization refocusing. Magn. Reson. Med. 6(2), 175–193 (1988).
7. Carr HY: Steady-state free precession in nuclear magnetic resonance. Phys. Rev. Lett. 112, 1693–1701 (1958).

• First occurance of balanced steady-state free precession (SSFP) in the NMR literature, more than 50 years ago. Carr presents an impressively comprehensive description of the primary effects studied subsequently in MRI.

8. Oppelt A, Graumann R, Barfuss H, Fischer H, Hartl W, Shajor W: FISP – a new fast MRI sequence. Electromedica 54, 15–18 (1986).
9. Scheffler K, Lehnhardt S: Principles and applications of balanced SSFP techniques. Euro. Radiol. 13(11), 2409–2418 (2003).
10. Gyngell M: The application of steady-state free precession in rapid 2DFT NMR imaging: FAST and CE-FAST sequences. Magn. Reson. Imaging 6, 415–419 (1988).
11. Hennig J: Echoes: How to generate, recognize, use or avoid them in MR-imaging sequences. Concepts Magn. Reson. 3, 125–143 (1991).

• Describes the mechanisms of echo formation over multiple repetition time (TR) periods. Provides an excellent primer on the topic of coherence pathways, which are crucial to understanding this signal formation.

12. Deimling M, Heid O: Magnetization prepared true FISP imaging. Proceedings of the 2nd International Society for Magnetic Resonance in Medicine. San Francisco, CA, USA, 6–12 August 1994.
13. Nishimura DG, Vasanawala S: Analysis and reduction of the transient response in SSFP imaging. Proceedings of the 8th International Society for Magnetic Resonance in Medicine. Denver, CO, USA, 1–7 April 2000.
14. Hargreaves BA, Vasanawala SS, Pauly JM, Nishimura DG: Characterization and reduction of the transient response in steady-state MR imaging. Magn. Reson. Med. 46(1), 149–158 (2001).
15. Bieri O, Scheffler K: Flow compensation in balanced SSFP sequences. Magn. Reson. Med. 54(4), 901–907 (2005).

• Highlights the subtleties in achieving true flow insensitivity with balanced SSFP in order to avoid image artifacts.

16. Storey P, Li W, Chen Q, Edelman RR: Flow artifacts in steady-state free precession cine imaging. Magn. Reson. Med. 51, 115–122 (2004).
17. Ernst R, Anderson W: Application of Fourier transform spectroscopy to magnetic resonance. Rev. Sci. Instruments 37, 93–102 (1966).
18. MacKay AL, Whittall KP, Adler J, Li D, Paty D, Graeb D: In vivo visualization of myelin water in brain by magnetic resonance. Magn. Reson. Med. 31, 673–677 (1994).
19. Stanisz GJ, Kecojevic A, Bronskill M, Henkelman RM: Characterizing white matter with magnetization transfer and T₂. Magn. Reson. Med. 42, 1128–1136 (1999).
20. Mehta RC, Pike GB, Enzmann DR: Magnetization transfer magnetic resonance imaging: a clinical review. Topics Magn. Res. Imaging 8, 214–230 (1996).
21. Christensen K, Grant D, Schulman E, Walling C: Optimal determination of relaxation times of Fourier transform nuclear magnetic resonance. Determination of spin-lattice relaxation times in chemically polarized species. J. Phys. Chem. 78, 1971–1977 (1974).
22. Fram E, Herfkens R, Johnson G et al.: Rapid calculation of T₁ using variable flip angle gradient refocused imaging. Magn. Reson. Imaging 5, 201–208 (1987).
23. Wang H, Riederer S, Lee JN: Optimizing the precision in T₁ relaxation estimation using limited flip angles. Magn. Reson. Med. 5, 399–416 (1987).

• Early and readable paper describing the use of Christensen’s variable flip-angle T₁-mapping method in an imaging context.

24. Homer J, Beevers M: Driven-equilibrium single-pulse observation of T₁ relaxation. A re-evaluation of a rapid “new” method for determining NMR spin-lattice relaxation times. J. Magn. Reson. 63, 287–297 (1985).
25. Wang J, Qiu M, Kim H, Constable R: T₁ measurements incorporating flip angle calibration and correction in vivo. J. Magn. Reson. 182, 283–292 (2006).
26. Cheng HM, Wright G: Rapid high-resolution T₁ mapping by variable flip angles: accurate and precise measurements in the presence of radiofrequency field inhomogeneity. Magn. Reson. Med. 55, 566–574 (2006).
27. Yarnykh VL: Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 57(1), 192–200 (2006).
28. Deichmann R, Haase A: Quantification of T₁ values by SNAPSHOT-FLASH NMR imaging. J. Magn. Reson. 96, 608–612 (1992).
29. Scheffler K, Hennig J: T₁ quantification with inversion recovery trueFISP. Magn. Reson. Med. 45(4), 720–723 (2001).
30. Wolff SD, Balaban RS: Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn. Reson. Med. 10, 135–144 (1989).
31. Pike GB: Pulsed magnetization transfer contrast in gradient echo imaging: a two-pool analytic description of signal response. Magn. Reson. Med. 35, 95–103 (1996).

• Describes the theoretical steady-state signal equation for the magnetization transfer spoiled-gradient echo sequence based on the two-pool, coupled Bloch equations.

32. Sled JG, Pike GB: Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn. Reson. Med. 46, 923–931 (2001).
33. Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ: Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn. Reson. Imaging 20, 721–731 (2002).
34. Yarnykh VL: Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: theory and clinical applications. Magn. Reson. Med. 47, 929–939 (2002).
35. Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ: Quantitative interpretation of magnetization transfer. Magn. Reson. Med. 29, 759–766 (1993).
36. Bieri O, Mamisch T, Trattnig S, Scheffler K: Steady state free precession magnetization transfer imaging. Magn. Reson. Med. 60(5), 1261–1266 (2008).
37. Gloor M, Scheffler K, Bieri O: Quantitative magnetization transfer imaging using balanced SSFP. Magn. Reson. Med. 60(3), 691–700 (2008).
38. Gloor M, Scheffler K, Bieri O: Nonbalanced SSFP-based quantitative magnetization transfer imaging. Magn. Reson. Med. 64(1), 149–156 (2010).
39. Deoni SC, Rutt BK, Peters TM: Rapid combined T₁ and T₂ mapping using gradient recalled acquisition in the steady state. Magn. Reson. Med. 49(3), 515–526 (2003).
40. Schmitt P, Griswold M, Jakob P et al.: Inversion recovery TrueFISP: quantification of T₁, T₂ and spin density. Magn. Reson. Med. 51, 661–667 (2004).
41. Vasanawala SS, Pauly JM, Nishimura DG: Linear combination steady-state free precession MRI. Magn. Reson. Med. 43(1), 82–90 (2000).
42. Deoni SCL: Transverse relaxation time (T₂) mapping in the brain with off-resonance correction using phase-cycled steady-state free precession imaging. J. Magn. Reson. Imaging 30(2), 411–417 (2009).
43. Crooijmans H, Gloor M, Bieri O, Scheffler K: Influence of MT effects on T₂ quantification with 3D balanced steady-state free precession imaging. Magn. Reson. Med. 65(1), 195–201 (2010).
44. Bieri O, Scheffler K: Effect of diffusion in inhomogeneous magnetic fields on balanced steady-state free precession. NMR Biomed. 20, 1–10 (2007).
45. Deoni SCL, Rutt BK, Jones DK: Investigating exchange and multicomponent relaxation in fully-balanced steady-state free precession imaging. JMRI 27(6), 1421–1429 (2008).
46. Lenz C, Klarhöfer M, Scheffler K: Limitations of rapid myelin water quantification using 3D bSSFP. MAGMA 23(3), 139–151 (2010).
47. Bieri O, Scheffler K: SSFP signal with finite RF pulses. Magn. Reson. Med. 62, 1232–1241 (2009).
48. Ogawa S, Lee T-M, Nayak AS, Glynn P: Oxygenation-sensitive contrast in magnetic resonance images of rodent brain at high magnetic fields. Magn. Reson. Med. 14, 68–78 (1990).
49. Thulborn KR, Waterton JC, Matthews PM, Radda GK: Oxygenation dependence of the transverse relaxation time of water protons in whole blood at high field. Biochim. Biophys. Acta 714, 265–270 (1982).
50. Scheffler K, Seifritz E, Bilecen D et al.: Detection of BOLD changes by means of a frequency-sensitive TrueFISP technique: preliminary results. NMR Biomed. 14, 490–496 (2001).

• First paper to propose using balanced SSFP to detect frequency shifts in vivo, forming the basis of many of the functional MRI (fMRI) and susceptibility techniques presented in this article.

51. Miller KL, Hargreaves BA, Lee J, Ress D, deCharms RC, Pauly JM: Functional MRI using a blood oxygenation sensitive steady state. Magn. Reson. Med. 50, 675–683 (2003).
52. Bowen CV, Menon RS, Gati JS: High field balanced-SSFP FMRI: A BOLD technique with excellent tissue sensitivity and superior large vessel suppression. In: Proceedings of the 13th International Society for Magnetic Resonance in Medicine. Miami, FL, USA, 7–13 May 2005.
53. Miller KL, Smith SM, Jezzard P, Wiggins GC, Wiggins CJ: Signal and noise characteristics of SSFP FMRI: a comparison with GRE at multiple field strengths. NeuroImage 37, 1227–1236 (2007).
54. Lee JH, Dumoulin SO, Saritas EU et al.: Full-brain coverage and high-resolution imaging capabilities of passband BSSFP FMRI at 3T. Magn. Reson. Med. 59(5), 1099–110 (2008).
55. 55 Dharmakumar R, Hong J, Brittain JH, Plewes DB, Wright GA: Oxygen-sensitive contrast in blood for steady-state free precession imaging. Magn. Reson. Med. 53(3), 574–583 (2005).
56. Zhong K, Leupold J, Hennig J, Speck O: Systematic investigation of balanced steady-state free precession for functional MRI in the human visual cortex at 3 Tesla. Magn. Reson. Med. 57(1), 67–73 (2007).
57. Barth M, Meyer H, Kannengiesser SAR, Polimeni JR, Wald LL, Norris DG: T₂-weighted 3D fMRI usingS2-SSFP at 7 tesla. Magn. Reson. Med. 63(4), 1015–1020 (2010).
58. Miller KL, Jezzard P: Modeling SSFP functional MRI contrast in the brain. Magn. Reson. Med. 60, 661–673 (2008).

• Discusses the broad range of contrast mechanisms contributing to fMRI contrast in balanced SSFP (both transition and pass band), relevant to other sources of susceptibility contrast, as well.

59. Ganter C: Static susceptibility effects in balanced SSFP sequences. Magn. Reson. Med. 56, 687–691 (2006).
60. Buracas GT, Liu TT, Buxton RB, Frank LR, Wong EC: Imaging periodic currents using alternating balanced steady-state free precession. Magn. Reson. Med. 59(1), 140–148 (2007).
61. Miller KL, Smith SM, Jezzard P, Pauly JM: High-resolution FMRI at 1.5 T using balanced SSFP Magn. Reson. Med. 55, 161–170 (2006).
62. Parrish T, Chen Y, Li W, Howard J, Gottfried J: High resolution 3D functional images of the human olfactory bulb using passband SSFP at 3T. Proc. ISMRM 16, 3567 (2008).
63. Muir E, Park S, Duong T: Pass-band balanced steady state free precession functional MRI of the mouse retina. Proc. ISMRM 1208 (2010).
64. Lee J, Santos JM, Conolly SM, Miller KL, Hargreaves BA, Pauly JM: Respiratoryinduced B0 field fluctuation compensation in balanced SSFP: real-time approach for transition-band SSFP FMRI. Magn. Reson. Med. 55, 1197–1201 (2006).
65. Wu ML, Wu PH, Huang TY et al.: Frequency stabilization using infinite impulse response filterin for SSFP FMRI at 3T. Magn. Reson. Med. 57, 369–379 (2007).
66. Tijssen RH, Smith SM, Jezzard P, Frost R, Jenkinson M, Miller KL: Characterization and correction of physiological instabilities in 3D FMRI. Proceedings of the 18th International Society for Magnetic Resonance in Medicine, Stockholm, Sweden, 1163, 1–7 May 2010.
67. Haacke EM, Xu Y, Cheng YCN, Reichenbach JR: Susceptibility-weighted imaging (SWI). Magn. Reson. Med. 52, 612–618 (2004).
68. Duyn DH, Gelderen PV, Li T, de Zwart J, Koretsky A, Fukunaga M: High-field MRI of brain cortical substructure based on signal phase. Proc. Natl Acad. Sci. 104, 11796–11801 (2007).
69. Peters AM, Brookes MJ, Hoogenraad FG et al.: T₂* measurements in human brain at 1.5, 3 and 7 T. Magn. Reson. Imaging 25, 748–753 (2007).
70. Cherubini A, Peran P, Hagberg GE et al.: Characterization of white matter fiber bundles with T₂* relaxometry and diffusion tensor imaging. Magn. Reson. Med. 61, 1066–1072 (2009).
71. Fukunaga M, Lee J, Li T-Q et al.: Layerspecific variation of iron content in cerebral cortex as a source of MRI contrast. Proc. Natl Acad. Sci. USA 107(8), 3834–3839 (2010).
72. He X, Yablonskiy DA: Biophysical mechanisms of phase contrast in gradient echo MRI. Proc. Natl Acad. Sci. 106, 13558–13563 (2009).
73. Dubois J, Lethimonnier F, Vaufrey F, Robert P, Bihan DL: Frequency-shift based detection of BMS contrast agents using SSFP: potential for MRA. Magn. Reson. Imaging 23, 453–462 (2005).
74. Foster-Garaeu P, Heyn C, Alejski A, Rutt B: Imaging single mammalian cells with a 1.5 T clinical MRI scanner. Magn. Reson. Med. 49(5), 968–971 (2003).
75. Dharmakumar R, Koktzoglou I, Li D: Generating positive contrast from offresonant spins with steady-state free precession magnetic resonance imaging: theory and proof-of-principle experiments. Phys. Med. Biol. 51(17), 4201–4215 (2006).
76. Cukur T, Yamada M, Overall W, Yang P, Nishimura D: Positive contrast with alternating repetition time SSFP (PARTS): a fast imaging technique for SPIO-labeled cells. Magn. Reson. Med. 63(2), 427–437 (2010).
77. Lee J, Shahram M, Schwartzman A, Pauly JM: Complex data analysis in high-resolution SSFP FMRI. Magn. Reson. Med. 57, 905–917 (2007).
78. Lee J, Fukunaga M, Duyn JH: Improving contrast-to-noise ratio of resonance frequency contrast images (phase images) using balanced steady-state free precession. NeuroImage 54, 2779–2788 (2011).
79. Wu ML, Young GS, Chen NK: Midbrain nuclei visualization improved by susceptibility-enhanced 3D multi-echo SSFP for deep brain stimulation guidance. Program and Abstratcs of the ISMRM 18th Meeting. Stockholm, Sweden, 1–7 May 2010 (Abstract 701).
80. Miller KL: Asymmetries of the balanced SSFP profile. Part I: theory and observation. Magn. Reson. Med. 63, 385–395 (2010).
81. Miller KL, Smith SM, Jezzard P: Asymmetries of the balanced SSFP profile. Part II: white matter. Magn. Reson. Med. 63, 396–406 (2010).
82. Li TQ, van Gelderen P, Merkle H, Talagala L, Koretsky AP, Duyn J: Extensive heterogeneity in white matter intensity in high-resolution T₂*-weighted MRI of the human brain at 7T. NeuroImage 32, 1032–1040 (2006).
83. Stejskal EO, Tanner JE: Spin-diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 19(4), 306–317 (1965).
84. Turner R, LeBihan D, Maier J, Vavrek R, Hedges LK, Pekar J: Echo-planar imaging of intravoxel incoherent motion. Radiology 177, 407–414 (1990).
85. LeBihan D: Intravoxel incoherent motion imaging using steady-state free precession. Magn. Reson. Med. 7, 346–351 (1988).
86. Merboldt KD, Hanicke WH, Gyngell ML, Frahm J, Bruhn H: Rapid NMR imaging of molecular self-diffusion using a modified CE-FAST sequence. J. Magn. Reson. 82, 115–130 (1989).
87. Buxton RB: The diffusion sensitivity of fast steady-state free precession imaging. Magn. Reson. Med. 29, 235–243 (1993).

• Presents an intuitive description of the diffusion-weighted steady-state signal based on coherence pathway components.

88. Kaiser R, Barthold E, Ernst RR: Diffusion and field-gradient effects in NMR Fourier spectroscopy. J. Chem. Phys. 60(8), 2966–2979 (1974).
89. Merboldt KD, Hanicke W, Gyngell ML, Frahm J, Bruhn H: The influence of flow and motion in MRI of diffusion using a modified CE-FAST sequence. Magn. Reson. Med. 12, 198–208 (1989).
90. Zur Y, Bosak E, Kaplan N: A new diffusion SSFP imaging technique. Magn. Reson. Med. 37, 716–722 (1997).
91. Miller KL, Pauly JM: Nonlinear phase correction for navigated diffusion imaging. Magn. Reson. Med. 50, 343–353 (2003).
92. McNab JA, Gallichan D, Miller KL: 3D steady-state diffusion-weighted imaging with trajectory using radially-batched internal navigator echoes (TURBINE). Magn. Reson. Med. 63, 235–242 (2010).
93. Jung Y, Samsonov AA, Block WF et al.: 3D diffusion tensor MRI with istoropic resolution using a steady-state radial acquisition. J. Magn. Reson. Imaging 29, 1175–1184 (2009).
94. Lee H, Price RR: Diffusion imaging with the MP-RAGE sequence. 4(6), 837–842 (1994).
95. Norris DG, Driesel W: Online motion correction for diffusion-weighted imaging using navigator echoes: application to RARE imaging without sensitivity loss. Magn. Reson. Med. 45, 729–733 (2001).
96. Jeong EK, Kim SE, Parker DL: Highresolution diffusion-weighted 3D MRI, using diffusion-weighted driven equilibrium (DW-DE) and multishot segmented 3D-SSFP without navigator echoes. Magn. Reson. Med. 50, 821–829 (2003).
97. Sinha U, Sinha S: High-speed diffusion imaging in the presence of eddy currents. J. Magn. Reson. Imaging 6, 657–666 (1996).
98. McNab JA, Miller KL: Steady-state diffusion-weighted imaging: theory, acquisition and analysis. NMR Biomed. 23(7), 781–793 (2010).
99. Parker DL, Yuan C, Blatter DD: MR angiography by multiple thin slab 3D acquisition. Magn. Reson. Med. 17(2), 434–451 (1991).
100. Carr JC, Simonetti O, Bundy J, Li D, Pereles S, Finn JP: Cine MR angiography of the heart with segmented true fast imaging with steady-state precession. Radiology 219(3), 828–834 (2001).
101. Korosec FR, Frayne R, Grist TM, Mistretta CA: Time-resolved contrastenhanced 3D MR angiography. Magn. Reson. Med. 36(3), 345–351 (1996).
102. Edelman RR, Siewert B, Adamis M, Gaa J, Laub G, Wielopolski P: Signal targeting with alternating radiofrequency (STAR) sequences: application to MR angiography. Magn. Reson. Med. 31(2), 233–238 (1994).
103. Hori M, Shiraga N, Watanabe Y et al.: Time-resolved three-dimensional magnetic resonance digital subtraction angiography without contrast material in the brain: initial investigation. J. Magn. Reson. Imaging 30(1), 214–218 (2009).
104. Overall WR, Conolly SM, Nishimura DG, Hu BS: Oscillating dual-equilibrium steady-state angiography. Magn. Reson. Med. 47(3), 513–522 (2002).
105. Yan L, Wang S, Zhuo Y et al.: Unenhanced dynamic MR angiography: high spatial and temporal resolution by using true FISP-based spin tagging with alternating radiofrequency. Radiology 256(1), 270–279 (2010).

• A nice demonstration of cerebral angiography using a catalyzed balanced SSFP acquisition in conjunction with inversion preparation.

106. Overall WR, Nishimura DG, Hu BS: Fast phase-contrast velocity measurement in the steady state. Magn. Reson. Med. 48(5), 890–898 (2002).
107. Markl M, Alley MT, Pelc NJ: Balanced phase-contrast steady-state free precession (PC-SSFP): a novel technique for velocity encoding by gradient inversion. Magn. Reson. Med. 49(5), 945–952 (2003).
108. Santini F, Wetzel SG, Bock J, Markl M, Scheffler K: Time-resolved three-dimensional (3D) phase-contrast (PC) balanced steady-state free precession (bSSFP). Magn. Reson. Med. 62(4), 966–974 (2009).
109. Markl M, Alley MT, Elkins CJ, Pelc NJ: Flow effects in balanced steady state free precession imaging. Magn. Reson. Med. 50(5), 892–903 (2003).
110. Boss A, Martirosian P, Klose U, Nagele T, Claussen CD, Schick F: FAIR-TrueFISP imaging of cerebral perfusion in areas of high magnetic susceptibility differences at 1.5 and 3 Tesla. J. Magn. Reson. Imaging 25(5), 924–931 (2007).