Research Article - Diabetes Management (2019) Volume 9, Issue 1
Relationship of body mass index with diabetes and breast cancer biomarkers
- Corresponding Author:
- Rabindra Nath Das
Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
E-mail: rabin.bwn@gmail.com
Abstract
Body mass index (BMI=Weight(kg)/Height(m2) is generally computed for each patient under some clinical studies, considering that it may be related with the disease. The report has derived the effects of BMI on diabetes & breast cancer markers for some cancer patients with the help of probabilistic modeling. It has been obtained that mean BMI is positively associated with fasting glucose (p=0.0753), insulin (p=0.0002), leptin (p<0.0001), monocyte chemoattractant protein-1 (MCP-1) (p=0.0002), and it is negatively associated with homeostasis model assessment score (HOMA) (p<0.0001), adiponectin (p=0.0003), and class of patients (p=0.0116). The variance of BMI is partially positively associated with age (p=0.1751), and it is negatively associated with resistin (p=0.1450) and insulin (p=0.2413). These three variance explanatory factors are known as confounder according to Epidemiology. Therefore, high BMI increases glucose, insulin, leptin, MCP-1, and it decreases HOMA & adiponectin.
Keywords
adiponectin, body mass index, biomarker, breast cancer, insulin, leptin, non-constant variance
Introduction
For any individual under clinical treatment, four absolute physical units such as weight, height, hip and waist are generally measured, assuming that these may be associated with the considered study disease. With the help of these measures, the relative measure body mass index (BMI= Weight(kg)/Height(m)2) is computed. Note that BMI is a composite measure, which is used in examining as a determinant of the interested study disease. Generally, it represents an index of fatness of an individual. It is widely used as a risk factor for the development of many diseases such as diabetes, cardiovascular diseases, breast cancer etc. [1-10]. The relationship between BMI and cardiovascular diseases has been focused in many articles based on proportions, logistic regression, simple correlation and regression, which are not appropriate in many cases [1-3]. But there is a little study based on probabilistic modeling, regarding the relationship of BMI with many cardiac parameters such as systolic blood pressure (BP), diastolic BP, basal BP, maximum BP, mean arterial pressure, mean central venous pressure, heart rate (HR), basal HR, peak HR, maximum HR, ejection fraction, cardiac index etc. The relationship between BMI and many diabetes markers such as fasting glucose, HbA1c, 2-hours post plasma glucose, random plasma glucose, along with other necessary explanatory variables are very little known in the medical literature based on probabilistic modeling [11,12]. Some articles have shown that (BMI & fasting glucose), (BMI & insulin) are positively associated based on simple correlation & regression, modeling with or without including other explanatory variables [7,9,11,13,14]. The relationship between BMI with breast cancer biomarkers such as leptin, resistin, MCP-1, HOMA, adiponectin is little known based on probabilistic modeling [15,16]. There is a little study regarding the relationship of BMI with diabetes and breast cancer biomarkers based on probabilistic modeling in medical literature. The report aims to establish the relationship of BMI with diabetes & breast cancer biomarkers based on probabilistic modeling. It searches the response of the following hypotheses. What is the relationship of BMI with diabetes & breast cancer biomarkers? What are the associations of BMI with diabetes & breast cancer biomarkers? What are the effects of BMI on the diabetes & breast cancer biomarkers? These hypotheses will be inquired in the report with a real data set of 116 women along with 10 study characters.
Material & Statistical Methods
Materials
The report includes a data set of 116 (52 healthy controls & 64 breast cancer patients) women along with 10 (9 continuous & 1 attribute) study characters which is available in the UCI Machine Learning Repository. The subjects (study population), covariates and data collection process have been clearly expressed [15]. These are not repeated herein. Specifically, there are many research articles based on the Wisconsin Diagnosis Breast Cancer (WDBC), Wisconsin Breast Cancer Dataset (WBCD), and Wisconsin Prognosis Breast Cancer (WPBC) data sets [16-18]. For the immediate using of the covariates in the report, they are restated as AGE (years), BMI (kg/m2) GLUCOSE (mg/dL), INSULIN (μU/mL), HOMA, LEPTIN (ng/mL), (ADIPONECTIN) (μg/ mL), RESISTIN (ng/mL), MCP-1(pg/dL), Patient type (CLASS) (1=Healthy controls; 2= Breast cancer patients).
Statistical methods
The main purpose of the report is to establish the relationship of BMI with diabetes & breast cancer biomarkers along with age and types of patient. The study random variable is BMI (in the report), and the considered data set is a multivariate data [15]. The relationship of BMI is only can be established through probabilistic modeling. Note that the response BMI is a continuous, positive, non-constant variance, and non-normally distributed random variable. It may be modeled by suitable transformation if the variance is stabilized under the transformation. If the variance is not stabilized, it may be modeled by joint generalized linear models (JGLMs) with Log-normal and Gamma distributions, which are neatly expressed in [19-22]. These are not reproduced in the report. For detailed ideas about JGLMs, interested readers may go through [19,22].
Statistical & graphical analysis
The BMI is the interested response random variable which is identified as heteroscedastic, and it is not stabilized with any suitable transformation. BMI is considered as the dependent variable and the rest other 9 factors are used as the explanatory variables. BMI has been modeled by JGLMs adopting both Log-normal & Gamma distributions. The appropriate model has been selected based on the smallest Akaike information criterion (AIC) value (within each class), which minimizes both the squared error loss and predicted additive errors [23, p. 203-204]. In the mean model, one partially significant factor (Insulin), and in the variance model three partially significant factors (Age, Resistin, Insulin) are included for better fitting [23,24]. In Epidemiology, the partially significant included effects (here Age, Resistin, Insulin) in the model are known as confounders. The analysis results are displayed in TABLE 1. From TABLE 1, it is noted that Log-normal fit (AIC= 613.9) is better than Gamma fit (AIC=615.062) based on AIC rule.
| Model | Covariates | Log-normal | Gamma | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | s.e. | t-value | p-Value | Estimate | s.e. | t-value | p-Value | ||
| Mean | Constant | 3.0370 | 0.08364 | 36.312 | <0.0001 | 3.0460 | 0.08368 | 36.401 | <0.0001 |
| GLUCOSE (x3) | 0.0015 | 0.00085 | 1.796 | 0.0753 | 0.0016 | 0.00084 | 1.850 | 0.0670 | |
| INSULIN (x4) | 0.0123 | 0.00319 | 3.850 | 0.0002 | 0.0121 | 0.00317 | 3.828 | 0.0002 | |
| HOMA (x5) | -0.0421 | 0.01032 | -4.082 | <0.0001 | -0.0421 | 0.01018 | -4.133 | <0.0001 | |
| LEPTIN (x6) | 0.0053 | 0.00064 | 8.234 | <0.0001 | 0.0052 | 0.00064 | 8.095 | <0.0001 | |
| ADIPONECTIN (x7) | -0.0068 | 0.00183 | -3.736 | 0.0003 | -0.0068 | 0.00185 | -3.655 | 0.0004 | |
| MCP-1 (x9) | 0.0001 | 0.00004 | 3.872 | 0.0002 | 0.0001 | 0.00004 | 3.727 | 0.0003 | |
| CLASS (Fx10) | -0.0708 | 0.02757 | -2.568 | 0.0116 | -0.0699 | 0.02769 | -2.524 | 0.0130 | |
| Dispersion | Constant | -4.445 | 0.7260 | -6.122 | <0.0001 | -4.358 | 0.7166 | -6.082 | <0.0001 |
| AGE (x1) | 0.015 | 0.0107 | 1.365 | 0.1751 | 0.013 | 0.0106 | 1.265 | 0.2085 | |
| RESISTIN (x8) | -0.019 | 0.0132 | -1.468 | 0.1450 | -0.020 | 0.0132 | -1.508 | 0.1344 | |
| INSULIN (x4) | -0.018 | 0.0156 | -1.178 | 0.2413 | -0.019 | 0.0156 | -1.223 | 0.2239 | |
AIC= 613.9
AIC=615.062
Table 1: Results for mean and dispersion models for BMI from Log-Normal and Gamma fit
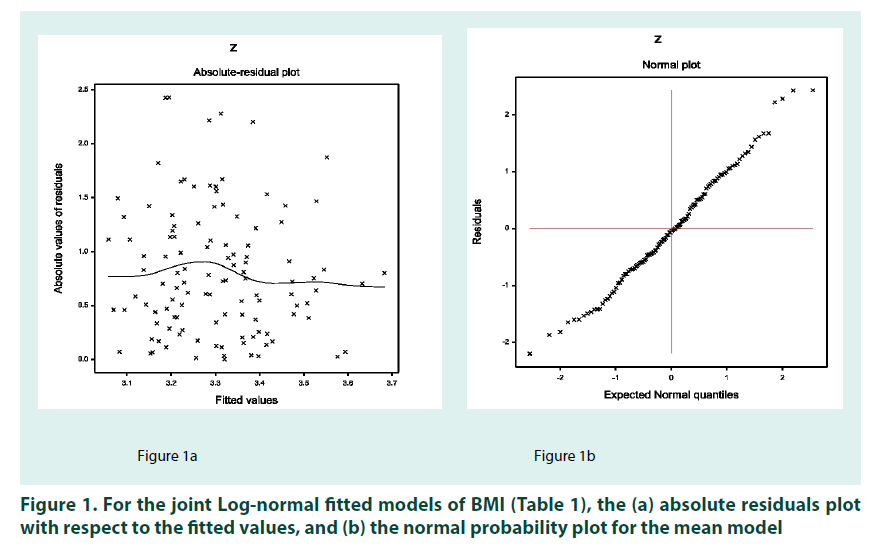
In practice, the valid conclusions are mainly drawn from the data generated model (or probabilistic model) which is assumed to be true. Therefore, the derived model is to be verified adopting model diagnostic tools. Here model diagnostic graphical analysis is applied for the final selected Log-normal fitted models (TABLE 1), which is displayed in FIGURE 1. The absolute residuals are plotted with respect to fitted values (for the fitted Lognormal models in TABLE 1) in FIGURE 1A, which is very closely linear, concluding that variance is constant with the running means. FIGURE 1B reveals the normal probability plot for the fitted Log-normal mean model (TABLE 1), which does not indicate any lack of fit. Therefore, both the figures prove that the fitted Log-normal model (TABLE 1) is approximately a true unknown BMI model.
Results
The analysis results of BMI under both the distributions are displayed in TABLE 1. Fitted Log-normal JGLMs are the accepted final models for BMI (TABLE 1). The following results are related to the fitted Log-normal models in TABLE 1. It has been derived that mean BMI is positively associated with fasten glucose (p=0.0753), insulin (p=0.0002), leptin (p<0.0001), monocyte chemoattractant protein-1 (MCP-1) (p=0.0002), and it is negatively associated with homeostasis model assessment score (HOMA) (p<0.0001), adiponectin (p=0.0003), and class of patients (p=0.0116). The variance of BMI is partially negatively associated with resistin (p=0.1450) & insulin (p=0.2413), and it is partially positively associated with age (p=0.1751).
Fitted Log-normal mean ( Zˆ ) model of BMI (from TABLE 1) is σˆ 2 = 3.0370 + 0.0015 GLUCOSE + 0.0123 INSULIN – 0.0421 HOMA + 0.0053 LEPTIN - 0.0068 ADIPONCTIN + 0.0001 MCP-1 – 0.0708 CLASS, and the fitted Lognormal variance (σˆ 2 ) model is σˆ 2= exp. (-4.445 + 0.015AGE – 0.019 RESISTIN - 0.018 INSULIN).
The mean & variance relationship of (Z=log BMI) are presented in the above by two equations. It is observed that mean BMI is explained by GLUCOSE, INSULIN, HOMA, LEPTIN, ADIPONCTIN, MCP-1 and CLSS, while variance of BMI is explained by AGE, RESISTIN, INSULIN.
Discussion
Final fitted results (TABLE 1) and the mean & variance models of BMI are given above. Lognormal fitted mean & variance models of BMI conclude the following.
1. The mean BMI (MBMI) is positively associated with glucose (p=0.0753), indicating that BMI increases as glucose rises.
2. MBMI is positively associated with insulin (p=0.0002), concluding that BMI rises as insulin increases.
3. MBMI is negatively associated with HOMA (p<0.0001), indicating that BMI increases as HOMA decreases.
4. MBMI is positively associated with leptin (p<0.0001), interpreting that BMI increases as leptin increases.
5. MBMI is negatively associated with adiponectin (p=0.0003), implying that BMI increases as adiponectin decreases.
6. MBMI is positively associated with MCP-1 (p=0.0002), concluding that BMI increases as MCP-1 increases.
7. MBMI is negatively associated with types of patient (1=healthy controls; 2= breast cancer patients) (p=0.0116), implying that BMI is higher for healthy individuals than patients.
8. Variance of BMI is partially positively associated with age (p=0.1751), implying that variance of BMI is higher at older ages.
9. Variance of BMI is partially negatively associated with resistin (p=0.1450), concluding that BMI variance increases as resistin decreases.
10. Variance of BMI is partially negatively associated with insulin (p=0.2413), indicating that BMI variance increases as insulin decreases.
Interpretations of the obtained results of BMI analysis have been discussed above. The associations and effects of BMI on diabetes and breast cancer biomarkers are described above clearly. The report shows that BMI increases if glucose, or insulin, or leptin or MCP-1 increases, or adiponectin, or HOMA, decreases. The associations of (BMI & glucose), (BMI & insulin) are positive which supports earlier findings [11,13]. This indicates that BMI is a risk factor for diabetes mellitus & insulin resistance or type 2 diabetes. The associations of BMI with adiponectin, leptin, resistin, MCP-1, and HOMA are not clearly given in earlier articles [5,6,16,18]. For this data set, it has been shown that BMI is lower for breast cancer women than normal. The present report shows that BMI & adiponectin are negatively associated, indicating that high BMI decreases the adiponectin level, where low adiponectin level is related with an increased breast cancer [25]. On the other hand, high adiponectin level is a protective factor for breast cancer, and it also reduces the BMI. The report shows BMI & leptin are highly positively associated, implying that high BMI increases the leptin level, where high leptin level is related with an increased breast cancer [26]. Again, the report shows that BMI and MCP-1 is positively associated, concluding that high BMI increases the MCP- 1 level, where high MCP-1 level is related with an increased breast cancer [27]. Note that BMI & HOMA is negatively associated, implying that high BMI decreases HOMA level, while low HOMA level is insulinsensitive (<1.0), and higher HOMA level (>1.9) indicates early insulin resistance [15,28]. This is a controversial role of BMI with HOMA. This invites to justify the homeostatic model assessment (HOMA) method for assessing β-cell function and insulin resistance (IR) from basal (fasting) glucose and insulin or C-peptide concentrations, along with BMI also. Note that HOMA model is controversial [28].
Conclusions
The effects of BMI on diabetes and breast cancer biomarkers have been derived in the report with the help of probabilistic modeling of BMI. The mean and variance models of BMI have been derived herein using JGLMs adopting both Log-normal and Gamma distributions. Final fitted model has been selected based on comparison of both the distributions, smallest AIC vale, graphical analysis, and small standard error of the estimates (TABLE 1). Note that both the distributions fitted models show similar results. Therefore, the interpretations regarding BMI have been derived herein based on approximately a true model. In addition, the derived outputs support earlier findings such as (BMI & glucose) and (BMI & insulin) are positively associated [2,4,11]. It has been derived that mean BMI is explained by glucose, insulin, HOMA, leptin, adiponectin, MCP-1, types of patient, while the variance of BMI has been explained by age, resistin and insulin.
The derived interpretations regarding BMI are associated with the data set given in [15]. The estimates may be different (only the values of regression coefficients) for different data set, but the nature of association of BMI with diabetes & breast cancer biomarkers will be identical. It has not been verified herein, as similar data sets are not available. In addition, the considered data set does not contain diabetes markers HbA1c, 2-hours post plasma glucose and random plasma glucose. Future research articles may consider all possible diabetes and breast cancer biomarkers along with age and BMI. The report shows that BMI is a risk factor for diabetes, insulin resistance (type 2 diabetes), and breast cancer also. It is obtained herein that high BMI increases glucose, insulin, leptin, MCP- 1, and it decreases adiponectin and HOMA. The role of BMI on HOMA looks little different than other cancer biomarkers. This is due to the problem of HOMA model, and the HOMA model to be considered again based on fasting glucose, insulin and BMI also (it is suggested based on the report). Note that reciprocal of the present HOMA model may act properly with BMI (it is suggested based on the report). Medical practitioners will be familiar regarding the association of BMI with diabetes & breast cancer biomarkers from the report, and every individual should reduce his/her BMI.
Conflict of interest
The authors confirm that this article content has no conflict of interest.
Acknowledgement
The authors are very much indebted to the referees who have provided valuable comments to improve this paper. This research was supported by the Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2014M3C7A1062896).
References
- Williams C, Hayman L, Daniels S et al. Cardiovascular health in childhood: A statement for health professionals from the Committee on Atherosclerosis, Hypertension, and Obesity in the Young (AHOY) of the Council on Cardiovascular Disease in the Young, American Heart Association. Circulation. 106(1), 143–160 (2002).
- US Dept Health and Human Services. The Surgeon General’s Call to Action to Prevent and Decrease Overweight and Obesity. Rockville, MD: US Department of Health and Human Services, Public Health Service, Office of the Surgeon General 2001.
- National Institutes of Health. Clinical guidelines on the identification, evaluation, and treatment of overweight and obesity in adults — the evidence report. Obes. Res. 6 (2), 51–209S (1998).
- Gunter M, Xie X, Xue X et al. Breast cancer risk in metabolically healthy but overweight postmenopausal women. Cancer. Res. 75(2), 270–274 (2015).
- Key T, Appleby P, Reeves G et al. Body mass index, serum sex hormones, and breast cancer risk in postmenopausal women. J. Natl. Cancer. Inst. 95(16), 1218–1226 (2003).
- Van den Brandt PA, Spiegelman D, Yaun S et al. Pooled analysis of prospective cohort studies on height, weight, and breast cancer risk. Am. J. Epidemiol. 152(6), 514–527 (2000).
- Bays H, Chapman R, Grandy S. The relationship of body mass index to diabetes mellitus, hypertension and dyslipidaemia: comparison of data from two national surveys. Int. J. Clin. Pract. 61(5), 737–747 (2007).
- American Diabetes Association. Diagnosis and classification of diabetes mellitus. Diabetes. Care. 29, S43–81 (2006).
- Gray N, Picone G, Yashkin A. The relationship between BMI and onset of diabetes mellitus and its Complications. South. Med. J. 108(1), 29–36 (2015).
- Stein C, Colditz G. The epidemic of obesity. J. Clin. Endocrinol. Metab. 89, 2522–2525 (2004).
- Das R. Diabetes and obesity determinants based on blood serum. Endocrinol. Diabetes. 2(2),1–6 (2016).
- Das R. Association between diabetes markers and cholesterol. Diabetes. Manag. 7(2), 247–249 (2017).
- World Health Organization. Obesity and Overweight Facts. http:// www.who.int/hpr/NPH /docs/gs_obesity.pdf (accessed March 2007).
- Flegal K, Graubard B, Williamson D et al. Excess deaths associated with underweight, overweight, and obesity. JAMA. 293, 1861–1867 (2005).
- Patrício M, Pereira J, Crisóstomo J et al. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC. Cancer . 18(1), 18-29 (2018).
- Wolberg W, Mangasarian O. Multi surface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 87(23), 9193–9196 (1990).
- Zheng B, Yoon S, Lam S. Breast cancer diagnosis based on feature extraction using a hybrid of K-means and support vector machine algorithms. Expert. Syst. Appl. 41(4), 1476–1482 (2014).
- Maglogiannis I, Zafiropoulos E, Anagnostopoulos I. An intelligent system for automated breast cancer diagnosis and prognosis using SVM based classifiers. Appl. Intell. 30(1), 24–36 (2009).
- Lee Y, Nelder J, Pawitan Y. Generalized linear models with random effects (Unified Analysis via H–likelihood). London: Chapman & Hall 2006.
- Das R, Lee Y. Log-normal versus gamma models for analyzing data from quality-improvement experiments. Qual. Eng.. 21(1), 79-87 (2009).
- Das R, Lee Y. Analysis strategies for multiple responses in quality improvement experiments. IJQET. 1(4), 395-409 (2010).
- Das R. Robust response surfaces, regression, and positive data analyses. London: Chapman & Hall 2014.
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, Springer-Verlag, 2001.
- Das R. Discrepancy in fitting between log-normal and gamma models: An illustration. Model Assisted Statistics and Applications 7 (1) 23–32 (2012).
- Macis D, Guerrieri-Gonzaga A, Gandini S. Circulating adiponectin and breast cancer risk: a systematic review and meta-analysis. Int. J. Epidemiol. 43(4), 1226–1236 (2014) .
- Niu J, Jiang L, Guo W et al. The association between leptin level and breast cancer: a meta-analysis. PloS. One. 8(6), e67349 (2013).
- Dutta P, Sarkissyan M, Paico K et al. MCP-1 is overexpressed in triple- negative breast cancers and drives cancer invasiveness and metastasis. Breast. Cancer. Res. Treat. 170(3), 477–486 (2018).
- Wallace TM, Levy JC, Matthews DR. Use and Abuse of HOMA Modeling. Diabetes. Care. 27(6), 1487–1495 (2004).