Research Article - Interventional Cardiology (2016) Volume 8, Issue 5
Hypertension risk factors who underwent dobutamine stress echocardiography
- Corresponding Author:
- Rabindra Nath Das
Department of Statistics, University of Burdwan, Golapbag, Rajbati, Burdwan, 713104, West Bengal, India
Tel: +919232638970
E-mail: rabin.bwn@gmail.com
Submitted: 26 August 2016; Accepted: 06 October 2016; Published online: 11 October 2016
Abstract
Objectives and methods: The present report aims to identify the hypertension risk factors who underwent Dobutamine stress echocardiography (DSE) (558 heart patients), based on the routine secondary data set (UCLA Statistics Web Site) without any specific setting. Joint generalized linear statistical gamma models are used. Results: The present identified statistical significant hypertension risk factors from three blood pressure (basal, systolic, and maximum) analyses are the following: basal heart rate (bhr) (P<0.0001), double product (DP) of basal blood pressure and heart rate (basedp) (P<0.0001), peak heart rate (pkhr) (P<0.0001), DP of peak heart rate & systolic blood pressure (dp) (P<0.0001), dobutamine dose (dose) (P=0.0268), maximum heart rate (maxhr) (P<0.0001), percent maximum predicted heart rate (pctM-phr) (P=0.0312), DP on maximum dobutamine dose and blood pressure (dpmaxdo) (P<0.0001), age (P=0.0048), chest pain (P=0.0505), resting wall motion abnormality on echocardiogram (restwma) (P<0.0001), positive stress echocardiogram (posSE) (P=0.0002), new myocardial infraction (newMI) (P<0.0001), recent angioplasty (newPTCA) (P=0.0252), recent bypass surgery (newCABG) (P=0.0482), history of hypertension (hxofHT) (P=0.0541), history of coronary artery bypass surgery (hxofCABG) (P=0.0529), any event (P=0.0289), and base line electrocardiogram diagnosis (ecg) (P=0.0312). Conclusions: Impacts of heart conditions, biochemical parameters, dobutamine dose and many others on hypertension have been identified based on probabilistic modeling. Most of the present findings and their effects are almost new in the hypertension literature.
Keywords
Biochemical parameters, Blood pressure, Gamma models, Hypertension, Lifestyle characteristics, Non-constant variance
Hypertension affects 30% of the adult population [1]. It is associated with stroke for 54%, and 47% of ischaemic heart disease [2]. Hypertension management is mainly done by pharmacotherapy. Despite the availability of numerous drugs, response rates to any given drug are approximately 50% and only one in three patients with hypertension has their blood pressure controlled to target [3]. Several studies have shown that up to 53% of patients with uncontrolled hypertension were non adherent to treatments [4,5]. Many factors (such as sleep apnoea, lifestyle and biochemical parameters) are responsible for uncontrolled blood pressure, and the intraindividual blood pressure variability [6] and the genetic effects [7] have a major impact on the determination of response to drugs.
The American Heart Association [8], and the European Society of Hypertension (ESH) [9] independently published the guidelines for self-monitoring of blood pressure by patients at home (HBPM) in 2008. These two guidelines recommended HBPM for long-term monitoring of treated hypertension and also for the initial diagnostic phase of subjects with elevated blood pressure (BP) [8,9]. Many studies examined the performance of HBPM in the diagnosis of hypertension phenotypes (sustained, white-coat, masked hypertension) in untreated and treated subjects, by taking ambulatory BP monitoring (ABPM) [10-15].
It is well-known that the hypertension is directly associated with stroke and ischemic heart disease, and the stroke is related with the blood pressure, so this report aims to identify the blood pressure risk factors of heart patients who underwent DSE. To identify the hypertension risk factors, early researches have used some statistical techniques (such as z-test, Chisquare test, Logistic regression, Odds ratio, Analysis of variance (ANOVA) and Classification & regression tree analysis (CART)) [16-20], which are inappropriate in many cases [21,22]. Many earlier hypertension articles have considered the response as dichotomous or continuous with constant variance, but some authors have noticed that the variance is non-constant. Yet only the mean model has been considered (assuming constant variance), which may lead erroneous results [22-24]. Therefore, the earlier findings invite some doubts and debates. A positive data set (a character which always takes positive values, for example, blood pressure) is generally analyzed either by the log-normal or the gamma model [21,25,26]. For a positive data set, the variance may be non-constant, as it may have relationship with the mean. The non-constant variance problem, which often occurs for non-Normal response variable, in linear regression is a departure from the standard least squares assumptions. The present data set is positive, its variance is non-constant, distribution is non-Normal, and the earlier used statistical methods are inappropriate. These issues have motivated us to identify the hypertension risk factors of the DSE data set [16], based on the basal, systolic and maximum blood pressure analyses. The present study has identified many hypertension risk factors of 558 patients who underwent DSE by separately analyzing the three blood pressure responses, namely, basal, systolic, and maximum, based on the remaining other explanatory variables (Table 1). All of these three non-replicated, positive response distributions are non-Normal with non-constant variances. Under these situations, what are the appropriate statistical modelling techniques for the DSE data set [16]? Joint generalized linear gamma model [24,27] is the most appropriate statistical technique for the DSE data set which is described in the following section.
| Variable | Operationalization | Mean (S.D.)/ |
|---|---|---|
| Name | Proportion | |
| bhr (y1) | Basal heart rate (bpm) | 75.29 (15.42) |
| basebp (y2) | Basal blood pressure (mmHg) | 135.3 (20.77) |
| basedp (x1) | Basal double product (DP) | 10181 (2579.75) |
| bhr¤basebp (bpm¤mmHg) | ||
| pkhr (x2) | Peak heart rate (bpm) | 120.6 (22.57) |
| sbp (x3) | Systolic blood pressure (mmHg) | 146.9 (36.53) |
| dp (x4) | DP pkhr¤sbp (bpm¤mmHg) | 17634 (5220.53) |
| dose (x5) | Dobutamine dose (DD) given | 33.75 (8.13) |
| maxhr (x6) | Maximum heart rate (bpm) | 119.4 (21.91) |
| pctMphr (x7) | Percent maximum predicted heart rate | 78.57 (15.12) |
| mbp (x8) | Maximum blood pressure (mmHg) | 156.0 (31.71) |
| dpmaxdo (x9) | DP on max DD (bpm¤mmHg) | 18550 (4901.43) |
| dobdose (x10) | DD at max double product (mg) | 30.24 (9.54) |
| age (x11) | Age (years) | 67.34 (12.05) |
| gender (F12) | Gender (male=0, female=1) | 0%=39.43, 1%=60.57 |
| baseEF (x13) | Baseline cardiac ejection fraction | 55.60 (10.32) |
| dobEF (x14) | Ejection fraction on dobutamine | 65.24 (11.76) |
| chestpain (F15) | Chest pain (yes (y)=0, no (n)=1) | 0%=69.18, 1%=30.82 |
| restwma (F16) | Resting wall motion abnormality | 0%=53.94 |
| on echocardiogram (ECDG) (y=0, n=1) | 1%=46.06 | |
| posSE (F17) | Positive stress ECDG (y=0, n=1) | 0%=75.63, 1%=24.37 |
| newMI (F18) new myocardial infraction (MI) (y=0, n=1) | 0%=94.98, 1%=5.02 | |
| newPTCA (F19) | Recent angioplasty (y=0, n=1) | 0%=95.16, 1%=4.84 |
| newCABG (F20) | Recent bypass surgery (y=0, n=1) | 0%=94.09, 1%=5.91 |
| death (F21) | death (y=0, n=1) | 0%=95.70, 1%=4.30 |
| hxofHT (F22) | History of hypertension (y=0, n=1) | 0%=29.57, 1%=70.43 |
| hxofDM (F23) | History of diabetes (y=0, n=1) | 0%=63.08, 1%=36.92 |
| hxofCig (F24) | History of smoking (non-smoker=0, | 0%=53.41, |
| moderate=1, heavy=2) | 1%=24.73, 2%=21.86 | |
| hxofMI (F25) | History of MI (y=0, n=1) | 0%=72.40, 1%=27.60 |
| hxofPTCA (F26) | History of angioplasty (y=0, n=1) | 0%=92.65, 1%=7.35 |
| hxofCABG (F27) | History of coronary artery | 0%=84.23 |
| bypass surgery (y=0, n=1) | 1%=15.77 | |
| any event (F28) | Death, newMI, newPTCA | 0%=84.05 |
| or newCABG (death=0, no=1) | 1%=15.95 | |
| ecg (F29) | Baseline electrocardiogram diagnosis | 0%=55.91 |
| (normal=0, equivocal=1, MI=2) | 1%=31.54, 2%=12.72 | |
Table 1: Operationalization of variables in the analysis.
Methodology: Joint Generalized Linear Gamma Models
In practice, many continuous positive responses have non-Normal error distributions, which are mostly analyzed by using the class of generalized linear models. For examples, the log-normal and gamma distributions, which are often useful for modeling positive data [25] that have variance-to-mean relationship, and the variance of the response may be non-constant. Nelder and Lee [28] proposed a modeling approach for the analysis of positive data yi’s. These researchers advocated the use of joint generalized linear models (JGLMs):
E(yi) = μi and Var(yi) = σ2iμ2i
where V(.) is the variance function and σ2 i’s are the dispersion parameters. In GLMs the variance consists of two components, V(μi) is the one depending upon the changes of the mean and σ2 i is the one independent of mean adjustment. In GLMs the variance function characterizes the distribution of GLM family. For example, the distribution is normal if V(μ) = 1, Poisson if V(μ) = μ, gamma if V(μ) = μ2, etc.
Joint models for the mean and dispersion parameters are
ηi = g(μi) = xtiβ and ξi = h(σ2 i) = witγ
where g(.) and h(.) are GLM link functions (i.e., the relationship between the mean and the linear predictors or the relationship between the variance and the linear predictors) for the mean and the dispersion, respectively, and xti and wit are the row vectors for regression models based on the levels of control variables. Maximum likelihood (ML) method is used for estimating the parameters of the mean model and restricted ML (REML) estimators are used for the dispersion model [22].
Data: The present study is based on the data set of 31 variables on 558 subjects (UCLA stress echocardiography data), from a total of 1183 patients referred to the UCLA Adult Cardiac Imaging and Hemodynamics Laboratories for DSE between March 1991 and March 1996. For each study unit, 31 characters (Table 1) have been recorded. In the given data set, there are only 558 subjects with all non-missing information, which is considered in the present analysis. A detailed description of the data set, collection method, patient population, and the DSE is given in [16]. This is not reproduced herein as it would increase the length of the paper. DSE is successfully and widely used to determine whether a patient with or without known coronary artery disease has ischemia [29-31].
Dependent variables: The present article has aimed to identify the risk factors of basal, systolic, and maximum blood pressure. Thus, we have considered three separate analyses. The first analysis considers basal blood pressure as the dependent variable, and the remaining others (Table 1) as the independent variables. Similarly, the second and the third analyses consider respectively, systolic and maximum blood pressure as the dependent variable, and the remaining others as the independent variables.
Independent variables: There are two sets of independent variables, qualitative and quantitative. Sixteen independent variables (Table 1) are qualitative and the remaining others are continuous variables. Table 1 presents a description of each set of item and how they are operationalized for the present study.
Descriptive statistics: Table 1 presents means and standard deviations of all the continuous variables, and the proportion of all the levels of the categorical variables. Average age of the present subject units is 67.34 years. Note that the percentages of female (60.57%) patients are greater than the male (39.43%). The percentages of the patients with chest pain, rest-wma, posSE, newMI, newPTCA and newCABG are respectively, 69.18%, 53.94%, 75.63%, 94.98%, 95.16%, and 94.09%. The objectives history of diabetes (hxofDM), hxofHT, hx-ofMI, hxofPTCA, and hxofCABG percentages are respectively, 63.08%, 29.57%, 72.40%, 92.65%, and 84.23%. Classified objectives as non-smoker, moderate and heavy percent-ages are respectively, 53.41%, 24.73%, and 21.86%. Status of ECG like as normal, equivocal, and MI percentages are respectively, 55.91%, 31.54%, and 12.72%. Now it is interesting to examine what are the statistical significant risk factors on basal, systolic, and maximum blood pressure? These issues are addressed in Sections 3.1, 3.2 and 3.3.
Basal Blood Pressure Analysis, Results and Interpretations
We have examined the basal, systolic, and maximum blood pressure responses using both the log-normal and the gamma models, which are generally used for modeling a positive data set [21,25,32,33]. These three response variables have been identified herein as nonconstant response variance. Moreover, the gamma model analysis gives better results than the log-normal model for each blood pressure. Therefore, only the gamma model analysis results are displayed for every case. This section presents the basal blood pressure analysis.
For factors, the constraint that the effects of the first levels are zero is accepted. There-fore, it is taken that the first level of each factor as the reference level by estimating it’s as zero. Suppose that αi for i = 1, 2, 3 represents the main effect of A. It is taken ᾶ1 = 0, so that ᾶ2 = ᾶ2-ᾶ1. For example, the estimate of the effect A2 means the effect of difference between the second and the first levels in the main effect A, i.e., ᾶ2-ᾶ1.
The continuous response basal blood pressure (with non-constant variance) has been modelled based on the remaining other explanatory variables, using the joint gamma models (Section 2), and the results are displayed in Table 2. The selected models have the smallest Akaike information criterion (AIC) value in each class. It is well known that AIC selects a model which minimizes the predicted additive errors and squared error loss [34]. Based on AIC ( = 3123.80), the final gamma fitted models (Table 2) have been selected. Some partially insignificant effects (hxofHT, ecg, hxoCig), known as confounder in epidemiology, are included in the model. Note that it is not necessary that all the selected effects in the models are significant [34]. The joint GLM diagnostic plots have been examined in Figure 1 for the fitted gamma models in Table 2.
| Covar. | estimate | s:e: | t | P-value | |
|---|---|---|---|---|---|
| Mean | Const. | 4.7439 | 0.0323 | 146.95 | <0.0001 |
| model | bhr (y1) | -0.0129 | 0.0002 | -76.86 | <0.0001 |
| basedp (x1) | 0.0001 | <0.0001 | 102.25 | <0.0001 | |
| maxhr (x6) | 0.0009 | 0.0003 | 3.45 | 0.0006 | |
| mbp (x8) | 0.0008 | 0.0002 | 4.28 | <0.0001 | |
| dpmaxdo (x9) | -0.0001 | <0.0001 | -3.98 | <0.0001 | |
| age (x11) | 0.0003 | 0.0001 | 2.83 | 0.0048 | |
| hxofHT (F221) | 0.0045 | 0.0028 | 1.59 | 0.1124 | |
| any event (F281) | -0.0079 | 0.0036 | -2.19 | 0.0289 | |
| ecg (F291) | 0.0039 | 0.0028 | 1.41 | 0.1591 | |
| ecg (F292) | 0.0056 | 0.0035 | 1.58 | 0.1147 | |
| Dispers. | Const. | -4.9622 | 0.7558 | -6.57 | <0.0001 |
| model | bhr (y1) | 0.0089 | 0.0053 | 1.67 | 0.0955 |
| pctMphr (x7) | -0.0377 | 0.0093 | -4.04 | <0.0001 | |
| mbp (x8) | -0.0142 | 0.0048 | -2.95 | 0.0033 | |
| dpmaxdo (x9) | 0.0001 | <0.0001 | 3.37 | 0.0008 | |
| newCABG (F201) | 0.5582 | 0.2819 | 1.98 | 0.0482 | |
| hxofCig (F241) | 0.2563 | 0.1502 | 1.71 | 0.0878 | |
| hxofCig (F242) | 0.1868 | 0.1638 | 1.14 | 0.2548 | |
| ecg (F291) | -0.1998 | 0.1371 | -1.46 | 0.1449 | |
| ecg (F292) | -0.4320 | 0.1998 | -2.16 | 0.0312 |
Table 2: Results for mean and dispersion models of basal blood pressure from gamma fit.
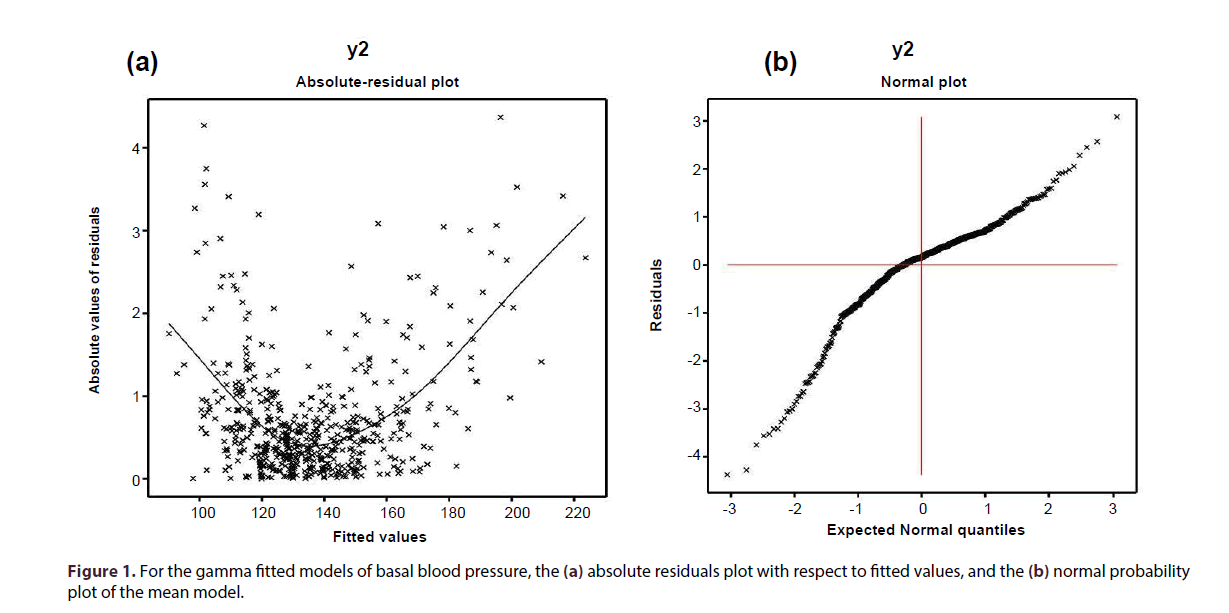
For the fitted gamma models (Table 2), the absolute residual values are plotted with respect to fitted values in Figure 1a. Note that the two left and right tails of the Figure 1a are respectively, decreasing and increasing, as the two boundary values are very large. But the middle part of the Figure 1(a) (covers most of the points) is a °at running means, an indication that the variance is not increasing with the mean values [22]. Figure 1b displays the normal probability plot of the fitted gamma mean model (Table 2), which does not show any lack of fit with respect to variables and outliers, as there is not any gap in the Figure.
In the gamma fitted mean model (Table 2), mean basal blood pressure (basebp) is separately positively associated with the basebp (P < 0.0001), maxhr (P = 0.0006), mbp (P < 0.0001) and age (P = 0.0048). Also mean basebp is separately negatively associated with the bhr (P < 0.0001), dpmaxdo (P < 0.0001) and any event (P = 0.0289). In the gamma fitted variance model (Table 2), basebp variance is separately positively associated with the dpmaxdo (P = 0.0008), newCABG (P = 0.0482), hxofCig (P = 0.0878). Also the basebp variance is separately negatively associated with the pctMphr (P < 0.0001), mbp (P = 0.0033) and ECG (P = 0.0312).
Each of basebp, maxhr, mbp, and age is separately positively associated with the mean basebp, indicating that as anyone of these increases, basebp increases. Note that basebp is a direct function of basedp, so they are positively associated. In practice, basebp is higher at older ages. The present findings satisfy the definition of mbp, function of basedp, and the risk factor age. Note that maxhr is higher at high basebp.
Also each of bhr, dpmaxdo and any event is separately negatively associated with the mean basebp, indicating that as anyone of these increases, basebp decreases. If basebp is low (<100 mmHg), bhr is very high (>80 times per minute) to deliver adequate oxygen to the body. It is also noted that the joint e®ect of higher dobutamine dose and mbp decreases the basebp. Mean basebp is higher at the lower level (0 = death) of the factor any event (due to negative association), indicating that the cardiac patient who dies with higher basebp.
Variance of basebp is separately positively associated with the bhr (partially), dp-maxdo, newCABG and hxofCig, indicating that as anyone of these increases, basebp variance also increases. Note that bhr has dual opposite e®ects with the mean and vari-ance of basebp, and the basebp variance is lower for the non-smoker or the cardiac patients having new CABG.
Again the basebp variance is separately negatively associated with the pctMphr, mbp and ecg, indicating that as anyone of these decreases, basebp variance also increases. Therefore, the basebp variance is higher of the cardiac patients having smaller pctMphr or mbp, or normal ecg status.
Systolic Blood Pressure Analysis, Results and Interpretations
The continuous response systolic blood pressure (non-constant variance) has been modelled based on the remaining other explanatory variables, using the joint gamma models, and the results are displayed in Table 3. The selected models have the smallest Akaike information criterion (AIC) value in each class. Based on AIC ( = 3693.52), the final gamma fitted models (Table 3) have been selected. Note that some nonsignificant effects are included in both the mean and variance models for proper fitting [34]. The joint GLM diagnostic plots have been examined in Figure 2, for the fitted gamma models in Table 3.
| Covar. | estimate | s:e: | t | P-value | |
|---|---|---|---|---|---|
| Mean | Const. | 3.8706 | 0.0521 | 74.25 | <0.0001 |
| model | bhr (y1) | -0.0010 | 0.0003 | -3.87 | 0.0001 |
| basedp (x1) | 0.0001 | <0.0001 | 3.17 | 0.0016 | |
| pkhr (x2) | -0.0089 | 0.0003 | -30.45 | <0.0001 | |
| dp (x4) | 0.0001 | <0.0001 | 52.28 | <0.0001 | |
| dose (x5) | 0.0005 | 0.0002 | 2.22 | 0.0268 | |
| maxhr (x6) | 0.0109 | 0.0005 | 20.14 | <0.0001 | |
| pctMphr (x7) | -0.0006 | 0.0003 | -2.16 | 0.0312 | |
| mbp (x8) | 0.0072 | 0.0003 | 22.50 | <0.0001 | |
| dpmaxdo (x9) | -0.0001 | <0.0001 | -23.98 | <0.0001 | |
| gender (F121) | -0.0055 | 0.0039 | -1.44 | 0.1504 | |
| chestpain (F151) | -0.0051 | 0.0037 | -1.38 | 0.1682 | |
| restwma (F161) | 0.0053 | 0.0045 | 1.19 | 0.2346 | |
| posSE (F171) | 0.0023 | 0.0047 | 0.49 | 0.6243 | |
| hxofHT (F221) | -0.0073 | 0.0038 | -1.93 | 0.0541 | |
| hxofCABG (F271) | -0.0047 | 0.0058 | -0.82 | 0.4126 | |
| ecg (F291) | 0.0017 | 0.0040 | 0.44 | 0.6601 | |
| ecg (F292) | 0.0060 | 0.0060 | 1.01 | 0.3129 | |
| Dispers. | Const. | -8.0260 | 0.8270 | -9.71 | <0.0001 |
| model | bhr (y1) | 0.035 | 0.0060 | 5.75 | <0.0001 |
| basebp (y2) | 0.0040 | 0.0040 | 1.02 | 0.3082 | |
| pctMphr (x7) | -0.019 | 0.0063 | -3.08 | 0.0022 | |
| age (x11) | 0.0091 | 0.0066 | 1.41 | 0.1591 | |
| chestpain (F151) | -0.3110 | 0.1589 | -1.96 | 0.0505 | |
| restwma (F161) | -1.0802 | 0.1566 | -6.89 | <0.0001 | |
| posSE (F171) | -0.3203 | 0.1762 | -1.82 | 0.0693 | |
| newMI (F181) | -1.9453 | 0.3307 | -5.88 | <0.0001 | |
| hxofHT (F221) | 0.6014 | 0.1668 | 3.61 | 0.0003 |
Table 3: Results for mean and dispersion models of systolic blood pressure from gamma fit.
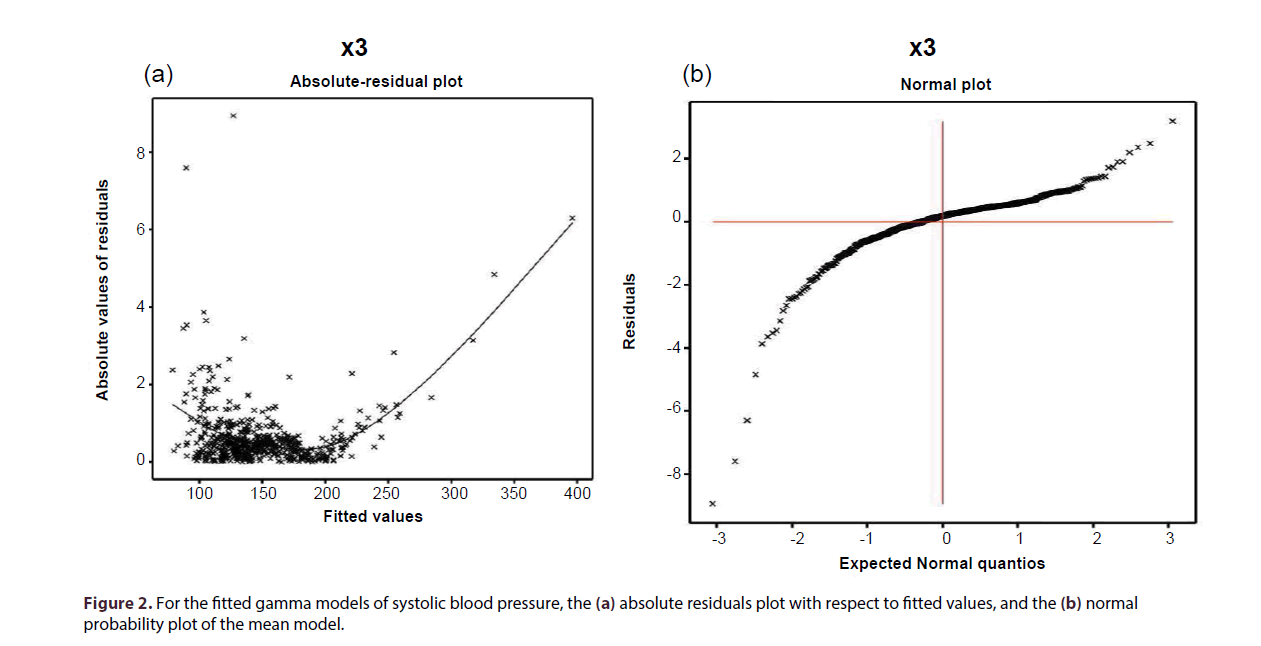
For the fitted gamma models (Table 3), the absolute residual values are plotted with respect to fitted values in Figure 2a. Its right tail is increasing due to the large right boundary value. All the parts of the Figure 2a (except the right tail) are a flat running means, an indication that the variance is not increasing with the mean values. Figure 2b displays the normal probability plot of the fitted gamma mean model (Table 3), which does not show any lack of fit with respect to variables and outliers, as there is not any gap in the Figure.
In the gamma fitted mean model (Table 3), mean sbp is separately positively associated with the basedp (P = 0.0016), dp (P < 0.0001), dose (P = 0.0268), maxhr (P < 0.0001) and mbp (P < 0.0001). Also the mean sbp is separately negatively associated with the bhr (P = 0.0001), pkhr (P < 0.0001), pctMphr (P = 0.0312), dpmaxdo (P < 0.0001) and hxofHT (P = 0.0541). Variance of sbp (Table 3) is separately positively associated with the bhr (P < 0.0001) and hxofHT (P = 0.0003), and it is separately negatively associated with the pctMphr (P = 0.0022), chestpain (P = 0.0505), restwma (P < 0.0001), posSE (P = 0.0693) and newMI (P < 0.0001).
The following main interpretations can be drawn from Table 3:
Each of basedp, dp, dose, maxhr, mbp is separately positively associated with the mean sbp, indicating that as anyone of these increases, mean sbp also increases. As basedp (dp) is a direct (or an indirect) function of sbp, so it is positively associated. Note that sbp is high at higher dobutamine dose (due to positive association). Positive association of mbp with the mean sbp satisfies the definition of mbp.
Again, each of bhr, pkhr, pctMphr, dpmaxdo, hxofHT and gender (partially) is negatively associated with the mean sbp, indicating that as anyone these decreases, sbp increases. For high sbp, bhr (also pkhr and pctMphr) is very low, so that heart fails to deliver adequate oxygen to the body. Also the interaction e®ect of higher dobutamine dose and mbp decreases the sbp. Due to inverse association, mean sbp is higher for a male than a female, or for a cardiac patient having hxofHT than a non-hxofHT patient.
Variance of sbp (Table 3) is separately positively associated with the bhr and hxofHT, indicating that as bhr or hxofHT-level increases, sbp variance also increases. Note that bhr has dual opposite effects with the mean and variance of sbp. Also, sbp variance is higher of the cardiac patients who have no hxofHT than the patients with hxofHT.
Also, sbp variance (Table 3) is separately negatively associated with the pctMphr, chestpain, restwma, posSE and newMI, indicating that as anyone these decreases, sbp variance increases. Here pctMphr has similar e®ects on both the mean and variance of sbp. Note that the sbp variance is higher of the cardiac patients having any one of these chestpain, restwma, posSE, and newMI.
Maximum Blood Pressure Analysis, Results and Interpretations
The continuous response maximum blood pressure (with non-constant variance) has been modelled based on the remaining other explanatory variables, using the joint gamma models, and the results are displayed in Table 4. The selected models have the smallest Akaike information criterion (AIC) value in each class. Based on AIC ( = 3365.36), the final gamma fitted models (Table 4) have been selected. Note that some nonsignificant effects are included in both the mean and the variance models for proper fitting [34]. The joint GLM diagnostic plots have been examined in Figure 3 for the fitted gamma models in Table 4.
| Covar. | estimate | s:e: | t | P-value | |
|---|---|---|---|---|---|
| Mean | Const. | 4.4084 | 0.0425 | 103.85 | <0.0001 |
| model | pkhr (x2) | 0.0045 | 0.0003 | 15.02 | <0.0001 |
| sbp (x3) | 0.0040 | 0.0002 | 23.91 | <0.0001 | |
| dp (x4) | -0.0001 | <0.0001 | -20.26 | <0.0001 | |
| maxhr (x6) | -0.0069 | 0.0007 | -10.47 | <0.0001 | |
| pctMphr (x7) | -0.0011 | 0.0009 | -1.24 | 0.2155 | |
| dpmaxdo (x9) | 0.0001 | <0.0001 | 59.71 | <0.0001 | |
| age (x11) | 0.0007 | 0.0005 | 1.51 | 0.1316 | |
| posSE (F171) | 0.0057 | 0.0026 | 2.24 | 0.0255 | |
| newPTCA (F191) | -0.0140 | 0.0058 | -2.44 | 0.0252 | |
| hxofCig (F241) | -0.0012 | 0.0029 | -0.42 | 0.6746 | |
| hxofCig (F242) | 0.0036 | 0.0033 | 1.09 | 0.2762 | |
| hxofMI (F251) | -0.0050 | 0.0029 | -1.72 | 0.0860 | |
| hxofCABG (F271) | -0.0067 | 0.0035 | -1.94 | 0.0529 | |
| Dispers. | Const. | 12.1391 | 2.5411 | 4.78 | <0.0001 |
| model | bhr (y1) | -0.2180 | 0.0334 | -6.54 | <0.0001 |
| basebp (y2) | -0.1433 | 0.0180 | -7.93 | <0.0001 | |
| basedp (x1) | 0.0021 | 0.0002 | 7.38 | <0.0001 | |
| pkhr (x2) | 0.0160 | 0.0106 | 1.47 | 0.1421 | |
| maxhr (x6) | -0.0232 | 0.0106 | -2.21 | 0.0275 | |
| chestpain (F151) | -0.2125 | 0.1476 | -1.44 | 0.1504 | |
| restwma (F161) | -0.3611 | 0.1597 | -2.26 | 0.0242 | |
| posSE (F171) | -0.6321 | 0.1666 | -3.79 | 0.0002 | |
| newCABG (F201) | -0.4270 | 0.2817 | -1.52 | 0.1291 |
Table 4: Results for mean and dispersion models of maximum blood pressure from gamma fit.
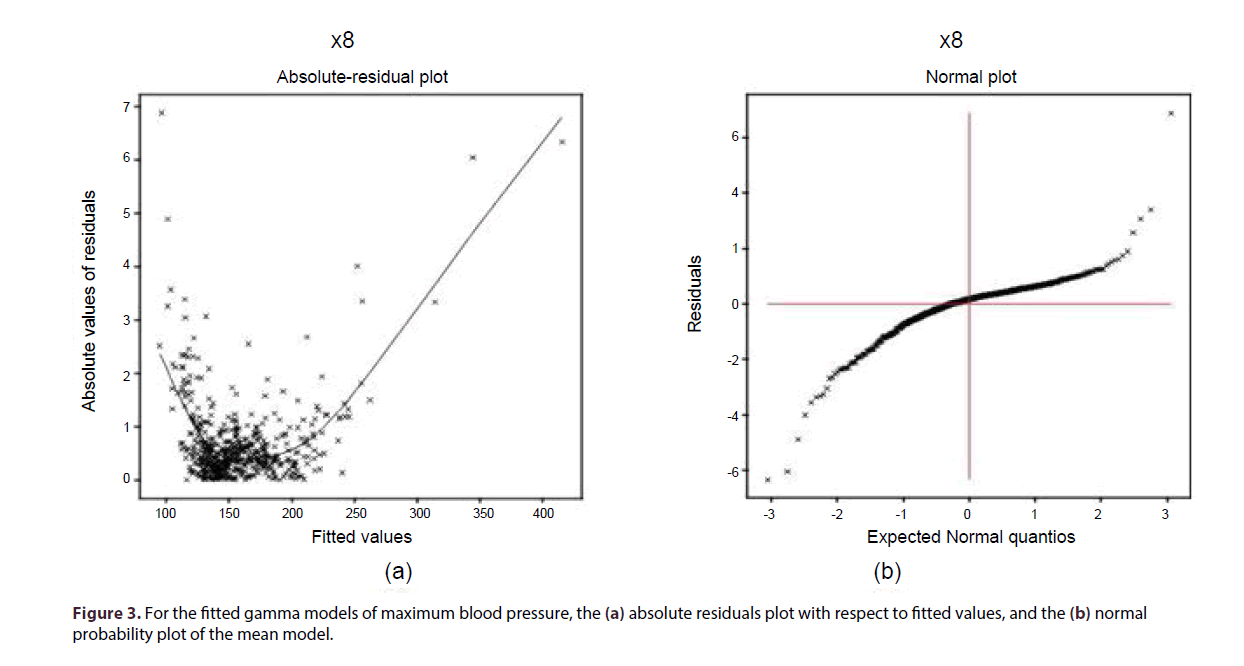
For the fitted gamma models (Table 4), the absolute residual values are plotted with respect to fitted values in Figure 3a. Its left and right tails are respectively, decreasing and increasing due to the two large boundary values at the two extremes. Its middle part which covers most of the points is a flat running means, an indication that the variance is not increasing with the mean values. Figure 3b displays the normal probability plot of the fitted gamma mean model (Table 3), which does not show any systematic departure, indicating no lack of fit.
In the gamma fitted mean model (Table 4), mean mbp is separately positively associated with the pkhr (P < 0.0001), sbp (P < 0.0001), dpmaxdo (P < 0.0001) and posSE (P = 0.0255). Also, the mean mbp is separately negatively associated with the dp (P < 0.0001), maxhr (P < 0.0001), newPTCA (P = 0.0252), hxofMI (P = 0.0860) and hxofCABG (P = 0.0529). Variance of mbp (Table 4) is separately negatively associated with the bhr (P < 0.0001), basebp (P < 0.0001), maxhr (P = 0.0275), restwma (P = 0.0242), posSE (P = 0.0002), and it is only positively associated with the basedp (P < 0.0001).
Each of pkhr, sbp, dpmaxdo, posSE and age (partially) is separately positively associated with the mean mbp, indicating that as anyone of these increases, mbp also increases. This implies, at higher value of mbp, pkhr is high as heart tries to deliver adequate oxygen to the body. Positive association of mbp with the sbp and dpmaxdo satisfies respectively, the mbp definition, and a direct functional relationship with dpmaxdo. Note that the mbp is higher of the cardiac patients who have no posSE, and also at older age, which is observed in practice.
Also, the mean mbp is separately negatively associated with the dp, maxhr, newPTCA, hxofMI and hxofCABG, indicating that as anyone of these decreases, mbp also increases. Note that dp ( = pkhr*sbp, Table 1) is inversely associated with the mbp (a direct function of sbp), satisfying the result that pkhr and sbp are oppositely associated (Table 3). Also the mbp is higher of the cardiac patients having at least any one of newPTCA, hxofMI and hxofCABG.
Variance of mbp is separately negatively associated with the bhr, basebp, maxhr, rest-wma and posSE, indicating that as anyone of these decreases, mbp variance increases. So, mbp variance is higher level for the smaller value of bhr, or basebp, or maxhr. Also the mbp variance is higher of the cardiac patients having restwma or posSE. Note that posSE has dual effects on both the mean and the variance of mbp. Variance of mbp is only positively associated with the basedp, indicating, mbp variance is higher for high value of basedp.
Discussion and Conclusion
The present report has identified many hypertension risk factors (Section 3) who underwent DSE based on the basal, systolic, and maximum blood pressure analyses of UCLA stress echocardiography data. In every case, the gamma model gives better results than the lognormal (not shown here), so only the gamma model results are displayed herein. One can verify the present results examining the data set given in (http://www.stat. ucla.edu:16080/projects/datasets/cardiacexplanation. html). Most of these derived results (Section 3) are new in hypertension literature. Specially, all the findings of the variance model are completely new. The present analyses have derived many interaction effects, which focus most probably the real practical situations.
All of the present findings are described in Section 3. There are many important results and conclusions in Section 3. From Table 2, it is observed that the basal blood pressure is directly associated with the maximum blood pressure and also age. At older age, the basal blood pressure will be high, and consequently, the maximum blood pressure will be also high (due to the positive association). Higher interaction effect of dobutamine dose and the maximum blood pressure (dpmaxdo) decreases the mean basal blood pressure, but this higher interaction effect increases the variance of the basal blood pressure. Also from Table 3, it is clear that the higher dobutamine dose increases the mean systolic blood pressure, while the higher dpmaxdo decreases the mean systolic blood pressure. From Table 4, it is noted that the higher dpmaxdo increases the maximum blood pressure. Note that the dobutamine dose and its interaction effect dpmaxdo have no effect on the variance of the systolic and maximum blood pressure. The present findings show that the role of dobutamine dose and its interaction effect is very complex on the blood pressure.
This report tries to fill some gaps of the hypertension literature by deriving the present results (Tables 2-4), which illuminate the complex relationships. Fortunately, a true mathematical model can open the truth that is covered by the complex relationships. Our research had two purposes. The first was to compare our results to those of previous research. A second purpose was to evaluate the statistical assumptions made by previous research regarding the hypertension determinants. Our concern was that previous research, making some inappropriate assumptions, would draw important conclusions from erroneous assumptions. As the given data set is positive heterogeneous, so only the gamma JGLM results are displayed, based on comparison with the log-normal (not shown).
The present results have been derived based on five criteria. First, is the comparison of both the log-normal and gamma models? Second, is the smallest AIC? Third, is very small standard deviation of the estimates (Tables 2-4), consequently, they are stable [22]. Fourth, is the regression diagnostic check by graphical analysis? Fifth, is the locating the appropriate dependent variable distribution.
These findings confirm some previous research findings, and they also try to remove some conflicts of earlier research findings (Section 3).
An important conclusion has to do with the use of earlier used statistical models. While further research is called for, we find that the gamma JGLMs are much more effective than either joint log-normal or many other traditional statistical techniques (pointed early), because they better fit the data. In short, research should have greater faith in these results than those emanating from the earlier models.
The findings of the present analyses along with the effects are described in Section 3. Medical practitioners and cardiac patients will be benefitted from these findings. Even though these findings are related with the DSE data set, yet the present report recommends the following for all individuals. Everyone should be very careful about blood pressure at older ages (Tables 2-4). A male individual is higher hypertension risk than a female (Table 3). Heart rate is closely related with the blood pressure (Tables 2-4), so care should be taken on both the blood pressure & heart rate, and they should be in control. Care should be taken on positive stress echocardiogram (Tables 3 and 4). Smoking should be stopped (Table 2). Medical practitioners should be care on dobutamine dose (Table 3), and its interaction effects with other risk factors (Tables 2-4), for better treatment. Cardiac events and the history of this disease should be considered by the medical practitioners and every cardiac patient (Tables 2-4).
Acknowledgement
The identity of the patient was absolutely preserved. The author is very much indebted to the referees who have provided valuable comments to improve this paper. The author also thanks Dr. Alan Garfinkel, UCLA School of Medicine, Department of Physiology, Los Angeles, California, USA, who generously provided the data sets to freely distribute and use for non-commercial purposes.
Executive summary
• Objectives and methods: The present report aims to identify the hypertension risk factors who underwent Dobutamine stress echocardiography (DSE) (558 heart patients), based on the routine secondary data set (UCLA Statistics Web Site) without any specific setting. Joint generalized linear statistical gamma models are used.
• Results: The present identified statistical significant hypertension risk factors from three blood pressure (basal, systolic, and maximum) analyses are the following: basal heart rate (bhr) (P < 0.0001), double product (DP) of basal blood pressure and heart rate (basedp) (P < 0.0001), peak heart rate (pkhr) (P < 0.0001), DP of peak heart rate & systolic blood pressure (dp) (P < 0.0001), dobutamine dose (dose) (P = 0.0268), maximum heart rate (maxhr) (P < 0.0001), percent maximum predicted heart rate (pctM-phr) (P = 0.0312), DP on maximum dobutamine dose and blood pressure (dpmaxdo) (P < 0.0001), age (P = 0.0048), chest pain (P = 0.0505), resting wall motion abnormality on echocardiogram (restwma) (P < 0.0001), positive stress echocardiogram (posSE) (P = 0.0002), new myocardial infraction (newMI) (P < 0.0001), recent angioplasty (newPTCA) (P = 0.0252), recent bypass surgery (newCABG) (P = 0.0482), history of hypertension (hxofHT) (P = 0.0541), history of coronary artery bypass surgery (hxofCABG) (P = 0.0529), any event (P = 0.0289), and base line electrocardiogram diagnosis (ecg) (P = 0.0312).
• Conclusions: Impacts of heart conditions, biochemical parameters, dobutamine dose and many others on hypertension have been identified based on probabilistic modeling. Most of the present findings and their effects are almost new in the hypertension literature.
References
- Kearney PM, Whelton M, Reynolds K, Muntner P, Whelton PK, He J. Global burden of hypertension: analysis of worldwide data. Lancet. 365, 217-223 (2005).
- Micha R, Wallace SK, Mozaffarian D. Red and processed meat consumption and risk of incident coronary heart disease, stroke, and diabetes mellitus: a systematic review and meta-analysis. Circulation. 121, 2271-2283 (2010).
- Falaschetti E, Chaudhury M, Mindell J, Poulter N. Continued improvement in hyper-tension management in England: results from the Health Survey for England 2006. Hypertension. 53, 480-486 (2009).
- Tomaszewski M, White C, Patel P, et al. High rates of nonadherence to antihy-pertensive treatment revealed by high-performance liquid chromatography-tandem mass spectrometry (HP LC-MS/MS) urine analysis. Heart. 100, 855-861 (2014).
- Jung O, Gechter JL, Wunder C, et al. Resistant hypertension? Assessment of adherence by toxicological urine analysis. J. Hypertens. 31, 766-774 (2013).
- Parati G, Ochoa JE, Lombardi C, Bilo G. Assessment and management of blood-pressure variability. Nat. Rev. Cardiol. 10, 143-155 (2013).
- Menni C. Blood pressure pharmacogenomics: gazing into a misty crystal ball. J. Hypertens. 33, 1142-1143 (2015).
- Pickering TG, Miller NH, Ogedegbe G, Krakoff LR, Artinian NT, Goff D. American Heart Association; American Society of Hypertension; Preventive Cardiovascular Nurses Association. Call to action on use and reimbursement for home blood pres-sure monitoring: a joint scientific statement from the American Heart Association, American Society of Hypertension, and Preventive Cardiovascular Nurses Association. Hypertension. 52, 10-29 (2008).
- Parati G, Stergiou GS, Asmar R, et al. ESH Working Group on Blood Pressure Monitoring. European Society of Hypertension guidelines for blood pressure monitoring at home: a summary report of the Second International Consensus Conference on Home Blood Pressure Monitoring. J. Hypertens. 26, 1505-1526 (2008).
- Stergiou GS, Bliziotis IA. Home blood pressure monitoring in the diagnosis and treatment of hypertension: a systematic review. Am. J. Hypertens. 24, 123-134 (2011).
- Stergiou GS, Kollias A, Zeniodi M, Karpettas N, Ntineri A. Home blood pressure monitoring: primary role in hypertension management. Curr.Hypertens. Rep. 16, 462-469 (2014).
- Stergiou GS, Zourbaki AS, Skeva II, Mountokalakis TD. White coat effect detected using self-monitoring of blood pressure at home: comparison with ambulatory blood pressure. Am. J. Hypertens.11, 820-827 (1998).
- Stergiou GS, Skeva II, Baibas NM, Kalkana CB, Roussias LG, Mountokalakis TD. Diagnosis of hypertension using home or ambulatory blood pressure monitoring: comparison with the conventional strategy based on repeated clinic blood pressure measurements. J. Hypertens. 18, 1745-1751 (2000).
- Masding MG, Jones JR, Bartley E, Sandeman DD. Assessment of blood pressure in patients with type 2 diabetes: comparison between home blood pressuremonitoring, clinic blood pressure measurement and 24 h ambulatory blood pressure monitoring. Diabet. Med. 18, 431-437 (2001).
- Hond ED, Celis H, Fagard R, et al.THOP investigators. Self-measured versus ambulatory blood pressure in the diagnosis of hypertension. J. Hypertens. 21, 717-722 (2003).
- Krivokapich J, Child JS, Walter DO, Garfinkel. Prognostic value of dobutamine stress echocardiography in predicting cardiac events in patients with known or suspected coronary artery disease. J. Am. Coll. Cardiol. 33(3), 708-716 (1999).
- Parati G, Ochoa JE, Lombardi C, Bilo G. Assessment and management of blood-pressure variability. Nat. Rev. Cardiol. 10, 143-155 (2013).
- Mena L, Pintos S, Queipo NV, Aizpurua JA, Maestre G, Sulbaran T. A reliable index for the prognostic significance of blood pressure variability. J. Hypertens.23, 505-511 (2005).
- Geleijnse ML, Fioretti PM, Roelandt JRTC. Methodology, feasibility, safety and diagnostic accuracy of dobutamine stress echocardiography. J. Am. Coll. Crdiol. 95, 1394-1401 (1997).
- Parati G, Rizzoni D. Assessing the prognostic relevance of blood pressure variability: discrepant information from different indices. J. Hypertens. 23, 483-486 (2005).
- Myers RH, Montgomery DC, Vining GG. Generalized Linear Models with Applica-tions in Engineering and the Sciences. John Wiley & Sons. NewYork, 2002.
- Lee Y, Nelder JA, Pawitan Y. Generalized Linear Models with Random Effects (Unified Analysis via H-likelihood). Chapman & Hall. London, 2006.
- Myers RH, Carter WH. Response surface techniques for dual response systems. Technometrics. 15, 301-317 (1973).
- Das RN, Lee Y. Analysis strategies for multiple responses in quality improvement experiments. Int. J. Qual. Engineering Techno. 1(4), 395-409 (2010).
- Firth D. Multiplicative errors: log-normal or gamma? J. R. Statist. Soc. B 50, 266-268 (1988).
- Das RN, Park JS. Discrepancy in regression estimates between log-normal and gamma: some case studies. J. Applied. Stats. 39(1), 97-111 (2012).
- Das RN, Lee Y. Log normal versus gamma models for analyzing data from quality-improvement experiments. Qual. Engineering. 21(1), 79-87 (2009).
- Nelder JA, Lee Y. Generalized linear models for the analysis of Taguchi-type exper-iments. Appl. Stochastic. Mod. Data Analy. 7, 107-120 (1991).
- Marcovitz PA, Armstrong WF. Accuracy of dobutamine stress echocardiography in detecting coronary artery disease. Am. J. Cardiol. 69, 1269-1273 (1992).
- Davila-Roman VG, Waggoner AD, Sicard GA, Geltman EM, Schechtman KB, Perez JE. Dobutamine stress echocardiography predicts surgical outcome in patients with an aortic aneurysm and peripheral vascular disease.J. Am. Coll. Cardiol. 21, 957- 963 (1993).
- Secknus MA, Marwick TH. Evolution of dobutamine echocardiography protocols and indications: safety and side effects in 3,011 studies over 5 years. J. Am. Coll. Cardiol. 29, 1234-1240 (1997).
- McCullagh P, Nelder JA. Generalized Linear Models. Chapman & Hall. London, 1989.
- Das RN. Robust Response Surfaces, Regression, and Positive Data Analyses. Chapman & Hall. London, 2014.
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Springer-Verlag. NewYork, 2001.