Clinical trial structures

*Corresponding Author:

Scott R. Evans, Ph.D.
Department of Statistics, Harvard University, 651 Huntington Avenue
FBX 513, Boston, MA, 02115.
Phone: 614.432.2998
Fax: 617.432.3163
Email: evans@sdac.harvard.edu

Abstract

Most errors in clinical trials are a result of poor planning. Fancy statistical methods cannot rescue design flaws. Thus careful planning with clear foresight is crucial. The selection of a clinical trial design structure requires log-ic and creativity. Common structural designs are discussed.

Keywords

p-value; confidence intervals; intent-to-treat; missing data; multiplicity; subgroup analyses; causa-tion

Introduction

Many structural designs can be considered when planning a clinical trial. Common clinical trial designs include single-arm trials, placebo-controlled trials, crossover trials, factorial trials, noninferiority trials, and designs for validating a diagnostic device. The choice of the structural design depends on the specif-ic research questions of interest, characteristics of the disease and therapy, the endpoints, the availabili-ty of a control group, and on the availability of funding. I discuss common clinical design structures, highlight their strengths, limitations, and assumptions, and provide guidance regarding when these designs may be considered in practice.

Common structural designs

Single-arm trials

The simplest trial design is a single-arm trial. In this design, a sample of individuals with the targeted medical condition is given the experimental therapy and then followed over time to observe their re-sponse. This design is employed when the objective of the trial is to obtain preliminary evidence of the efficacy of the treatment and to collect additional safety data, but is not generally used as confirmation of efficacy. The design may be desirable when the available patient pool is limited and thus it is not op-timal to randomize many participants to a control arm.

When designing single-arm trials, it is important to clearly define the goal or hypothesis of interest. For example, in a trial with a binary outcome (e.g., re-sponse vs. no response) the goal may be to show “any effect” (i.e., the null hypothesis is “zero response” or equivalently that the lower bound for the confi-dence interval for the response rate is greater than zero). A “minimum clinically relevant response rate” (rmin) would be identified to size the trial. The trial would be sized such that if the true response was rmin, then the probability of the lower bound of the confi-dence interval for the response rate being above zero (i.e., rejecting the null hypothesis of “zero response”) was equal to the desired power.

This trial design has several limitations and despite the design simplicity, the interpretation of the trial re-sults can be complicated. First, there is an inability to distinguish between the effect of the treatment, a pla-cebo effect, and the effect of natural history. Res-ponses could theoretically be due to the efficacy of the treatment, a placebo effect of an inefficacious therapy, or to a spontaneous or natural history im-provement. For a subject that has responded, it could be argued that the subject would have re-sponded even without treatment or that the subject responded because they thought that they were re-ceiving efficacious therapy. Furthermore, it is also difficult to interpret the response without a frame of reference for comparison. For example, if a trial is conducted and no change in the subject status is ob-served, then does this imply that the therapy is not helpful? It may be the case that if the subjects were left untreated then their condition would have wor-sened. In this case the therapy is having a positive effect, but this effect is not observable in a single-arm design.

Due to these limitations, single arm trials are best utilized when the natural history of the disease is well understood when placebo effects are minimal or non-existent, and when a placebo control is not ethically desirable. Such designs may be considered when spontaneous improvement in participants is not ex-pected, placebo effects are not large, and randomiza-tion to a placebo may not be ethical. On the other hand, such designs would not be good choices for trials investigating treatments for chronic pain be-cause of the large placebo effect in these trials.

Despite the limitations, single-arm trials may be the only (or one of few) options for trials evaluating ther-apies for which placebos are not ethical and options for controlled trials are limited. Single-arm trials have been commonly implemented in oncology. Oncology trials often employ a dose at or near the maximum tolerated dose (MTD, known from Phase I trials) to deliver the maximum effect and thus frequently em-ploy single dose trials. The primary endpoint is often tumor response, frequently defined as a percentage decrease in tumor size. Evans et.al. (Evans et al 2002) describes a Phase II trial evaluating low-dose oral etoposide for the treatment of relapsed or pro-gressed AIDS-related Kaposi’s sarcoma after sys-temic chemotherapy. The primary objective of the trial was to estimate the objective tumor response rate. A response was defined as at least a 50% de-crease in the number or size of existing lesions with-out the development of new lesions. A two-stage design was employed with the plan for enrolling 41 total subjects. However if there were no objective responses after the first 14 subjects have been eva-luated, then the trial would be discontinued for futility, noting that if the true response rate was at least 20%, then the probability of observing zero response in the first 14 subjects is less than 0.05. Notably, res-ponses were observed in the first 14 subjects, the trial continued, and etoposide was shown to be effec-tive. Recently the FDA also granted accelerated ap-proval of ofatumumab for the treatment of chronic lymphocytic leukemia refractory to fludarabine and alemtuzumab based on the results of a single-arm trial.

Placebo-controlled trials

Many trials are designed as placebo-controlled. Typi-cally a group of subjects with the target disease is identified and randomized to two or more treatments (e.g., active treatment vs. placebo). A randomized participant only receives one treatment (or treatment strategy) during the duration of the trial. Participants are then followed over time and the responses are compared between groups.

For example Evans (Evans et al 2007b) describes a randomized, double-blind, placebo-controlled, multi-center, dose-ranging study of prosaptide (PRO) for the treatment of HIV-associated neuropathic pain. Participants were randomized to 2, 4, 8, 16 mg/d PRO or placebo administered via subcutaneous in-jection. The objective was to compare each PRO dose group with placebo with respect to pain reduc-tion. The primary endpoint was the six week change from baseline in the weekly average of random daily Gracely pain scale prompts using an electronic diary. The study was designed to enroll 390 subjects equal-ly allocated between groups. The study was sized such that the 95% confidence interval for the difference between any dose arm and placebo with re-spect to changes in the 13-point Gracely pain scale was no wider than 0.24 assuming a standard devia-tion of Gracely pain scale changes of 0.35, an esti-mate derived from earlier studies.

Placebo-controlled designs are attractive since when they are utilized with randomization and the ITT prin-ciple, they allow for valid treatment group compari-sons. The disadvantage of parallel designs is that they can require large sample sizes due to the exis-tence of both within- and between-subject variation. Sample sizes can also be large when the desired effect size to detect is small.

Crossover trials

In a crossover design, each participant is randomized to a sequence of treatments that will be sequentially administered during treatment periods although the objective remains a comparison of treatments. For instance, in a two-period, two-sequence (2 x 2) cros-sover trial designed to compare two treatments A and B, a participant is randomized into one of two se-quences: (1) A then B, or (2) B then A. The randomi-zation of the treatment sequence helps to account for temporal trends (such as seasonal variation).

Crossover trials have several advantages. Firstly, they generally require fewer participants than parallel designs because each participant serves as his/her own control, thus eliminating inter-participant varia-tion. A crossover study may reduce the sample size of a parallel group study by 60-70% in some cases. Also since each participant is evaluated for each treatment, potentially confounding variables are ba-lanced between treatment groups by design, hence making treatment comparisons “fair”. Secondly, re-searchers can study individual participant response to treatment and examine participant-by-treatment interactions. Lastly, study recruitment may be en-hanced as potential participants are aware that they will receive active treatment at some point during the study.

However crossover trials should be used selectively. The primary concern with crossover trials is the po-tential “carry-over effect”. If the residual effect of the treatment provided in the first period continues into the second period when assessments of the second treatment are made (despite the discontinuation of the treatment at the end of the first period), then treatment comparisons could be biased since one cannot distinguish between the treatment effect and the carry-over effect. For this reason, a “washout” period is often built into the study design to separate two treatment periods to eliminate “carry-over” effects. A frequent recommendation is for the washout period to be at least 5 times the half-life of the treatment with the maximum half-life in the study. Endpoint evaluations can also be made at the end of a period to allow more time for the effects of prior treatments to dissi-pate. A second concern with crossover trials is the increased rate of participant drop-out. The drop-outs rate may be high in a crossover study since the trials are generally longer in duration for each participant, to accommodate for multiple treatment periods and associated washout periods. Participants are also exposed to more potentially harmful treatments and thus may be more likely to drop-out due to toxicity. The ramification of drop-outs in a crossover study is a threat to the generalizability of the study results as analyses are generally conducted on only the subset of participants that completed at least two periods.

Thus when conducting crossover trials it is important to take measures to minimize drop-out (e.g., diligent follow-up of participants). A strategy to replace par-ticipants that drop-out is frequently considered in or-der to maintain a balance in treatment comparisons. Period effects are also a concern in crossover trials. Furthermore the attribution of events can be compli-cated. Finally, the evaluation of long-term safety ef-fects is generally not possible. For these reasons, crossover trials are not generally appropriate for measuring long-term efficacy or safety effects and are rarely used in confirmatory Phase III trials.

Figure 1: ACTG A5252 crossover design schema

Crossover trials may therefore be an option when investigating therapies: (1) for chronic, stable diseas-es for which no permanent cure exists and for which the risk of death and subject drop-out is low, and (2) with a quickly reversible effect with treatment discon-tinuation, and (3) with a short half-life, and (4) with endpoints that have large inherent intra-subject varia-tion, and (5) with short treatment periods (i.e., treat-ment effects can be seen quickly).

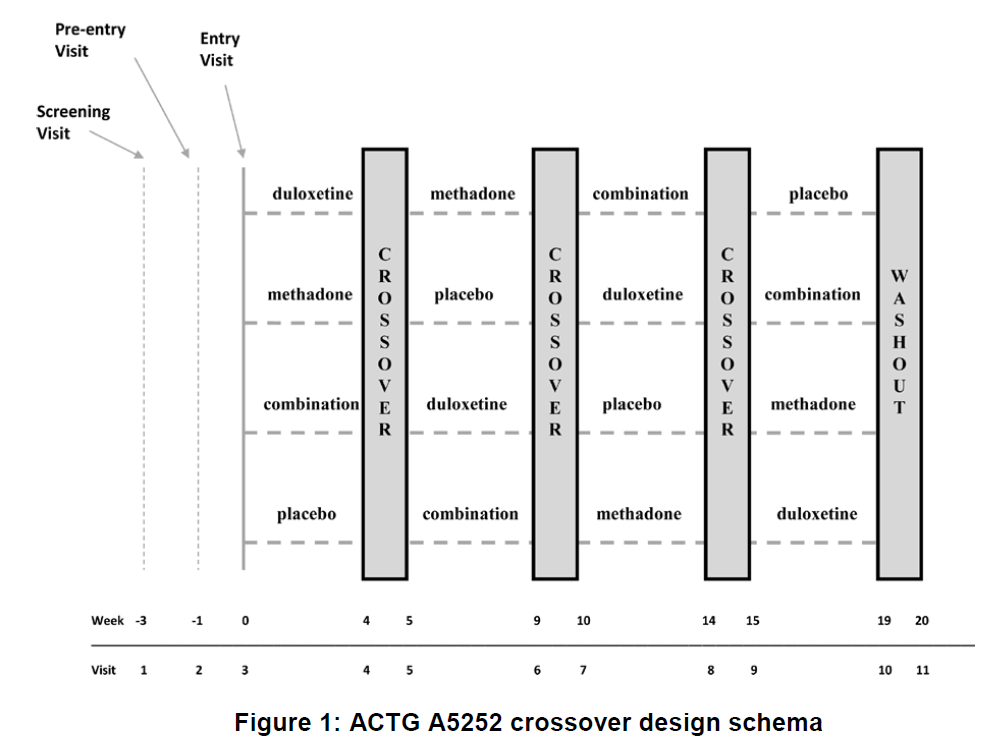
The AIDS Clinical Trials Group (ACTG) and the Neu-rologic AIDS Research Consortium (NARC) utilized a 4-period crossover design in a Phase II randomized, double-blind, placebo-controlled study (ACTG A5252) of combination analgesic therapy in HIV-associated painful peripheral neuropathy*. The trial investigated the use of methadone, duloxetine, and their combina-tion (vs. placebo) for the treatment of neuropathic pain associated with HIV. The design was appropri-ate since: (1) neuropathic pain is chronic, non-life threatening, non-curable, and relatively stable over time, (2) pain measurements are often subject to high intra-subject variation, (3) there is considerable con-cern for a placebo effect in studies of pain, and (4) pain generally returns to baseline levels with discon-tinuation of the treatments. To address the concern for potential carry over, a washout between each treatment period was implemented and pain was measured at the end of the treatment period to allow more time for residual effects to dissipate. Measures to minimize dropout included use of rescue medica-tion, follow-up calls to participants, a flexible titration schedule for study medications, and recommenda-tions for the management of treatment-emergent ad-verse events.

Factorial trials

Often a research team is interested in studying the effect of two or more interventions applied alone or in combination. In these cases a factorial design can be considered. Factorial designs are attractive when the interventions are regarded as having independent effects or when effects are thought to be complimen-tary and there is interest in assessing their interaction.

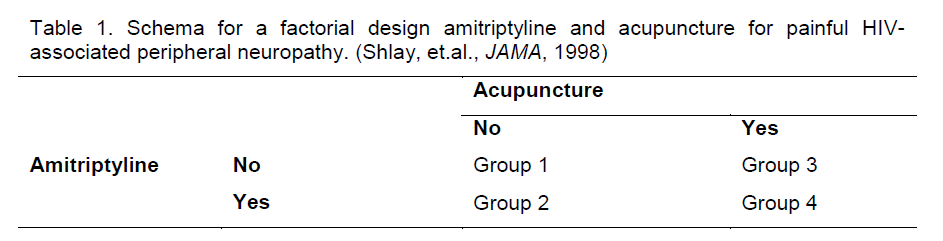
The simplest factorial design is a 2x2 factorial in which two interventions (factors) are being evaluated, each at two levels (e.g., intervention vs. no interven-tion). Each study participant is assigned to one level of each of the factors. Four intervention groups are defined based on whether they receive interventions A only, B only, both A and B, or neither A or B. Thus in order to apply the factorial design: (1) you must be able to apply the interventions simultaneously, and (2) it must be ethically acceptable to apply all levels of the interventions (e.g., including placebos if so de-signed). The factorial design can be viewed as an efficient way to conduct two trials in one. The factorial design is contraindicated when primary interest lies in comparing the two interventions to each other.

If one can assume that there is no interaction be-tween the two interventions, that is that the effect of one intervention does not depend on whether one receives the other intervention, then a factorial design can be more efficient than a parallel group design. Since factorial designs are economical, they are often employed when sample sizes are expected to be large as in prevention trials. One must first define the scale of measurement and distinguish between addi-tive and multiplicative interaction.

A limitation of factorial designs is that the assumption of no interaction is often not valid. The effect of one therapy often depends on whether the other therapy is provided. This limits the use of factorial designs in practice. Instances in which the no interaction as-sumption may be valid include the case when the two interventions have differing mechanisms of action (e.g., drug therapies combined with adjunctive thera-pies, complementary therapies, behavioral or exer-cise therapies, diet supplements, or other alternative medicines). For example, Bosch et.al. (Bosch et al 2002) conducted a factorial trial of ramipril and vita-min E for stroke prevention and Shlay et.al. (Shlay et al 1988) utilized a factorial design to study the effects of amitriptyline and acupuncture for the treatment of painful HIV-associated peripheral neuropathy (Table 1).

Table 1. Schema for a factorial design amitriptyline and acupuncture for painful HIV-associated peripheral neuropathy. (Shlay, et.al., JAMA, 1998)

Interestingly factorial designs are the only way to study interactions when they exist although their effi-ciency is deminished. They allow direct assessment of interaction effects since they include groups with all possible combinations of interventions. Combina-tion interventions are frequently of interest in medi-cine particularly when monotherapies are individually ineffective perhaps due to use of ceiling doses to limit toxicity, but complimentary mechanisms of action suggest potential synergistic effects. Quantitative in-teraction occurs when the effect of the combination intervention of A and B is greater than the effect of intervention A plus the effect of intervention B. Qua-litative interaction occurs when the effect of the com-bination intervention of A and B is less than the effect of intervention A plus the effect of intervention B. Having low power to detect interactions could result in incorrect characterization of intervention effects and sub-optimal patient care. Researcher should consider whether interactions are possible and ap-propriately size studies to detect interactions when their existence is unknown.

Factorial designs can be considered for more than two interventions. The Women’s Health Initiative (WHI) Clinical Trial utilized a 2x2x2 factorial design randomizing study participants to a dietary modifica-tion (low fat eating pattern vs. self-selected diet), hormone replacement therapy (HRT) vs. placebo, and calcium plus vitamin D supplement vs. placebo. However increasing the number of factors will in-crease the number of groups and associated com-plexity of the trial. Toxicity or feasibility constraints may also make it impossible to apply a full factorial design but incomplete factorial designs can be consi-dered although with increased complexity.

Also in factorial trials, the outcomes being studied may vary across interventions. In the WHI clinical trial, dietary modification was studied for its effect on breast and colorectal cancer, HRT was studied for its effect on cardiovascular disease risk, and calcium and vitamin D supplementation was studied for its effect on the risk for hip fractures.

Data monitoring of factorial designs can be compli-cated. Assigning attribution of the effects during the course of a trial can be difficult. It is not uncommon for one component of the trial to be terminated while other components continue, essentially viewing the factorial design as separate trials for each factor. The HRT component of the WHI was terminated due to an increased risk for breast cancer and overall health risks exceeding benefits. However, when con-sidering the termination of one component of the trial, an evaluation of the effect on power is critical. The termination of one component will reduce the power to detect interactions and will complicate analyses and subsequent interpretations of main effects and interactions.

Participant recruitment is more complex in factorial trials and can decrease accrual rates. Study partici-pants must meet criteria for treatment with each in-tervention with no contraindications to any of the possible treatment combinations, and have a willing-ness to consent to all of the interventions and proce-dures. Protocol adherence can also be more compli-cated due to the multiple interventions and greater burden on study participants. For these reasons it is important to monitor participant enrollment and adhe-rence.

When analyzing and reporting trials that utilize a fac-torial design, interaction effects should always be evaluated even if the trial was designed under the assumption of no interaction. Reporting should in-clude a transparent summary of each treatment cell so that potential interaction can be assessed. Re-searchers should be aware of the multiplicity issue given the assessment of multiple interventions. However, it is often considered desirable to control of the error rate for the assessment of each factor sepa-rately rather than controlling a trial-wise error rate. When interactions exist then it is inappropriate to in-terpret single global intervention effects. Instead one must estimate intervention effects conditional upon whether the other intervention is provided using sub-group analyses. For example there would be two ef-fects of intervention A: one for patients that receive intervention B and one for patients that do not receive intervention B.

Noninferiority trials

The rationale for noninferiority trials is that in order to appropriately evaluate an intervention, a comparison to a control group is necessary to put the results of an intervention arm into context. However for the targeted medical indication, randomization to a pla-cebo is unethical due to the availability of a proven effective therapy. In noninferiority trials, an existing effective therapy is selected to be the “active” control group. For this reason noninferiority trials are also called “active-controlled trials”.

The objective of a noninferiority trial is different than a placebo-controlled trial. No longer is it necessary to show that the intervention is superior to the control as in placebo-controlled trials, but instead it is desirable to show that the intervention is “at least as good as” or “no worse than” (i.e., noninferior to) the active con-trol. Hopefully the intervention is better than the ac-tive control in other ways (e.g., less expensive, better safety profile, better quality of life, different resistance profile, or more convenient or less invasive to administer such as requiring fewer pills or a shorter treat-ment duration resulting in better adherence). For ex-ample in the treatment of HIV, researchers seek less complicated or less toxic antiretroviral regimens that can display similar efficacy to existing regimens.

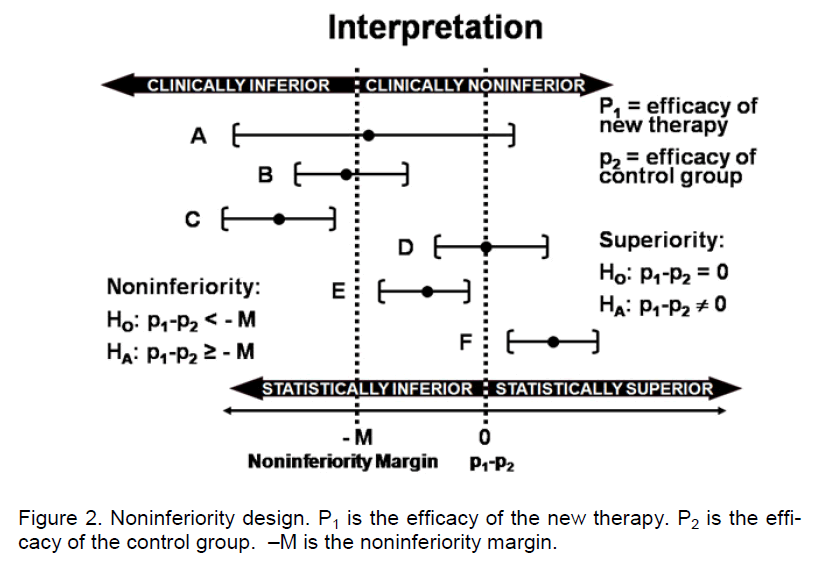
Noninferiority cannot be demonstrated with a non-significant test of superiority. The traditional strategy of a noninferiority trial is to select a noninferiority margin (M) and if treatment differences can be shown to be within the noninferiority margin (i.e., <M) then noninferiority can be claimed. The null and alternative hypotheses are H0: βT,active control ≥M and HA: βT,active control <M where βT,active control is the effect of the inter-vention therapy (T) relative to the active control. The standard analysis is to construct a confidence interval for the difference between arms and note whether the entire confidence interval is within the bounds of the noninferiority margin. For example if the primary end-point is binary (e.g., response vs. no response) then a confidence interval for the difference in response rates (intervention minus the active control) can be constructed. If the lower bound of the confidence in- terval is greater than –M, then important differences can be ruled out with reasonable confidence and noninferiority can be claimed. In Figure 2, confidence intervals A-F represent potential noninferiority trial outcome scenarios. The intervals have different cen-ters and widths. If the trial is designed to evaluate superiority, then a failure to reject the null hypothesis results from scenarios A and D (since the confidence interval does not exclude zero). Inferiority is con-cluded from scenarios B, C and E whereas superiori-ty is concluded from scenario F. If the trial is de-signed as a noninferiority trial, then a failure to reject the null hypothesis of inferiority results from scena-rios A, B, and C, but noninferiority is claimed in sce-narios D, E, and F since the lower bound of the inter-val is >-M. Some confusion often results from scena-rio E in which inferiority is concluded from a superiori-ty trial but noninferiority is concluded from a noninfe-riority trial. This case highlights the distinction be-tween statistical significance (i.e., the confidence in-terval excludes 0) and clinical relevance (i.e., the dif-ferences are less than M). Scenario A is a case in which neither superiority, inferiority, nor noninferiority can be claimed because the confidence interval is too wide. This may be due to a small sample size or large variation.

Figure 2. Noninferiority design. P1 is the efficacy of the new therapy. P2 is the effi-cacy of the control group. –M is the noninferiority margin.

Noninferiority clinical trials have become very com-mon in clinical research. Noninferiority trials can be “positive” resulting in claims of noninferiority or “nega-tive” resulting in an inability to make a noninferiority claim. The PROFESS study was a negative noninfe-riority trial with a time-to-event endpoint. The trial concluded that aspirin plus extended-release dipyri-damole was not noninferiority to clopidogrel for stroke prevention. The primary endpoint was recurrent stroke and a noninferiority margin was set at a 7.5% difference in relative risk. The 95% CI for the hazard ratio was (0.92, 1.11). Since the upper bound of the CI was greater than 1.075, noninferiority could not be concluded. By contrast, in a clinical trial evaluating treatments for newly diagnosed epilepsy, Keppra was shown to be noninferior to Carbatrol. The primary endpoint was 6 month freedom from seizure and a noninferiority margin was set at a 15% difference.

The 95% CI for the risk difference was (-7.8%, 8.2%) and thus noninferiority was concluded. (Brodie et al 2007)

Two important assumptions associated with the de-sign of noninferiority trials are constancy and assay sensitivity.

In noninferiority trials, an active control is selected because it has been shown to be efficacious (e.g., superior to placebo) in a historical trial. The constan-cy assumption states that the effect of the active con-trol over placebo in the historical trial would be the same as the effect in the current trial if a placebo group was included. This may not be the case if there were differences in trial conduct (e.g., differences in treatment administration, endpoints, or population) between the historical and current trials. This as-sumption is not testable in the current trial without a placebo group. The development of resistance is one threat to the constancy assumption.

To enable an evaluation of the retention of some of the effect of the active control over placebo, study participants, endpoints, and other important design features should be similar to those used in the trials for demonstrating the effectiveness of the active con-trol over placebo. One can then indirectly assess the constancy assumption by comparing the effective-ness of the active control in the noninferiority trial and the historical trial.

Noninferiority trials are appropriate when there is adequate evidence of a defined effect size for the active control so that a noninferiority margin can be justified. A comprehensive synthesis of the evidence that supports the effect size of the active control and the noninferiority margin should be assembled. For these reasons, the data many not support a noninfe-riority design for some indications.

“Assay sensitivity” is another important assumption in the design of noninferiority trials. The assumption of assay sensitivity states that the trial is designed in such a way that it is able to detect differences be-tween therapies if they indeed exist. Unless the in-strument that is measuring treatment response is sensitive enough to detect differences, then the ther-apies will display similar responses due to the insen-sitivity of the instrument, possibly resulting in erro-neously concluding noninferiority. The endpoints that are selected, how they are measured, and the con-duct and integrity of the trial can affect assay sensitiv-ity.

The active control in a noninferiority trial should be selected carefully. Regulatory approval does not necessarily imply that a therapy can be used as an active control. The active control ideally will have clin-ical efficacy that is: (1) of substantial magnitude, (2) estimated with precision in the relevant setting in which the noninferiority trial is being conducted, and (3) preferably quantified in multiple trials. Since the effect size of the active control relative to placebo is used to guide the selection of the noninferiority mar-gin, superiority to placebo must be reliably estab-lished and measured. Assurance that the active con-trol would be superior to placebo if a placebo was employed in the trial is necessary.

Recently there has been concern over the develop-ment of noninferiority studies using active controls that violate the constancy assumption (i.e., active control efficacy has changed over time) or that do not have proven efficacy over placebo. Research teams often claim that placebo controlled trials are not feas-ible because: (1) placebos are unethical because of the existence of other interventions, (2) patients are unwilling to enroll into placebo-controlled trials, and (3) Institutional Review Boards question the ethics of the use of placebos in these situations.

When selecting the active control for a noninferiority trial, one must consider how the efficacy of the active control was established (e.g., by showing noninfe-riority to another active control vs. by showing supe-riority to placebo). If the active control was shown to be effective via a noninferiority trial, then one must consider the concern for biocreep. Biocreep is the tendency for a slightly inferior therapy (but within the margin of noninferiority) that was shown to be effica-cious via a noninferiority trial, to be the active control in the next generation of noninferiority trials. Multiple generations of noninferiority trials using active con-trols that were themselves shown to be effective via noninferiority trials, could eventually result in the demonstration of the noninferiority of a therapy that is not better than placebo. Logically, noninferiority is not transitive: if A is noninferior to B, and B is noninferior to C, then it does not necessarily follow that A is non-inferior to C. For these reasons, noninferiority trials should generally choose the best available active controls.

The selection of the noninferiority margin in noninfe-riority trials is a complex issue and one that has created much discussion. In general, the selection of the noninferiority margin is done in the design stage of the trial and is utilized to help determine sample size. Defining the noninferiority margin in noninferiori-ty trials is context-dependent and it plays a direct role in the interpretation of the trial results. The selection of the noninferiority margin is subjective but struc-tured, requiring a combination of statistical reasoning and clinical judgment. Conceptually, one may view the noninferiority margin as the “maximum treatment difference that is clinically irrelevant” or the “largest efficacy difference that is acceptable to sacrifice in order to gain the advantages of the intervention”. This concept often requires interactions between statisti-cians and clinicians.

Since one indirect goal of a noninferiority trial is to show that intervention is superior to placebo, some of the effect of active control over placebo needs to be retained (often termed “preserving a fraction of the effect”). Thus the noninferiority margin should be se-lected to be smaller than the effect size of the active control over placebo. Researchers should review the historical data that demonstrated the superiority of the active control to placebo to aid in defining the noninferiority margin. Researchers must also consid-er the within and across-trial variability in estimates as well. Ideally the noninferiority margin should be chosen independent of study power, but practical limitations may arise since the selection of noninfe-riority margin dramatically affects study power.

One strategy for preserving the estimate of the effect is to set the noninferiority margin to a specific percen-tage (e.g., 50%) of the estimated active control effect vs. placebo. Alternatively the “95%-95% confidence interval method” could be used. In this strategy, the noninferiority margin is set to the lower bound of the 95% confidence interval for the effect of the active control vs. placebo. A poor choice of a noninferiority margin can result in a failed noninferiority trial. In the SPORTIF V trial, ximelegatran was compared to war-farin (active control) for stroke prevention in atrial fi-brillation patients. The event rate for warfarin was 1.2% and the noninferiority margin was set at 2% (absolute difference in event rates) based on historical data. Since the event rate in the warfarin arm was low, the noninferiority could be concluded even if the trial could not rule out a doubling of the event rate. For these reasons, the selection of the noninferiority margin should incorporate statistical considerations as well clinical relevance considerations.

A natural question is whether a noninferiority margin can be changed after trial initiation. In general there is little concern regarding a decrease in the noninfe-riority margin. However, increasing the noninferiority margin can be perceived as manipulation unless ap-propriately justified (i.e., based on external data that is independent of the trial).

The sample size depends upon the selection of the noninferiority margin and other parameters. Required sample sizes increase with a decreasing noninferiori-ty margin. Stratification can help since adjusted con-fidence intervals are generally narrower than unad-justed confidence intervals. Researchers should power noninferiority trials for a per protocol analyses as well as an intent-to-treat (ITT) analyses given the importance of both analyses (described later). Re-searchers also need to weigh the costs of Type I er-ror (i.e., incorrectly claiming noninferiority) and Type II error (i.e., incorrectly failing to claim noninferiority). One approach to sizing a noninferiority trial is to view the trial from an estimation perspective. The strategy is to estimate the difference between treatments with appropriate precision (as measured by the width of a confidence interval). Then size the study to ensure that the width of the confidence interval for the differ-ence between treatments is acceptable.

Interim analyses of noninferiority trials can be compli-cated. It generally takes overwhelming evidence to suggest stopping a trial for noninferiority during inte-rim analyses. Also there may not be an ethical im-perative to stop a trial that has shown noninferiority (in contrast to superiority studies with which if supe-riority is demonstrated, then there may be ethical im-peratives to stop the study since randomization to an inferior arm may be viewed as unethical). In addition even if noninferiority is demonstrated at an interim timepoint, it may be desirable to continue the study to assess whether superiority could be shown with trial continuation. It is not uncommon to stop a noninfe-riority trial for futility (i.e., unable to show noninferiori-ty). Use of repeated confidence intervals to control error rates with predicted interval plots (Evans et al 2007a; Li et al 2009) can aid data monitoring commit-tees with interim decision making.

The traditional approaches to the design and analys-es of noninferiority trials have been recently critiqued by noting a failure to distinguish between the two dis-tinct sub-objectives of noninferiority trials: (1) to dem-onstrate that the intervention is noninferior to the ac-tive control, and (2) to demonstrate that the interven-tion is superior to placebo taking into account histori-cal evidence. The design of a noninferiority trial can be accomplished by planning to test two separate hypotheses. A particular trial may only accomplish one of the two sub-objectives. If intervention is shown superior to placebo but fails to demonstrate noninfe-riority to the active control, then use of intervention may be indicated for patients that active control is contraindicated or not available. In contrast the inter-vention could be shown to be noninferiority to the active control but not superior to placebo. This may occur when the efficacy of the active control is mod-est. Recently there have been claims that the 2nd of the two sub-objectives (i.e., demonstrating superiority to placebo) is the objective of interest in the regulato-ry setting. Industry groups have argued that regulato-ry approval of new therapies should be based upon evidence of superiority to placebo (demonstration of clinically meaningful benefit) and not necessarily non-inferiority to an active control. Proponents of this perspective (often termed the “synthesis method”) pose several dilemmas and inconsistencies with tra-ditional approaches to noninferiority trials in support of this position. First, the intervention could look bet-ter than the active control but not meet the preserva-tion of effect condition. Second, two trials with differ-ent active controls have different standards for suc-cess. Third, if the intervention is shown to be superior to an active control then a natural question that arises is should the active control be withdrawn from the market? The basic argument is that the required de-gree of efficacy should be independent of the design (superiority vs. noninferiority) and that superiority to placebo is the standard for regulatory approval. Pro-ponents of the synthesis method thus argue that “noninferiority trial” terminology is inappropriate since the superiority of the intervention to placebo is the true objective.

One scientifically attractive alternative design is to have a 3-arm trial consisting of the intervention, the active control, and a placebo arm. This design is par-ticularly attractive when the efficacy of the active control has changed, is volatile, or is in doubt. This de-sign allows assessment of noninferiority and supe-riority to placebo directly, and allows for within-trial validation of the noninferiority margin. Unfortunately, this design is not frequently implemented due to a concern for the unethical nature of the placebo arm in some settings.

The choice of the noninferiority margin plays a direct role in the interpretation of the noninferiority trial, un-like the minimum clinically relevant difference that is often defined in superiority trials. Thus the justifica-tion for the noninferiority margin should be outlined in the analyses. The analysis of noninferiority trials also uses information outside of the current trial to infer the effect of the intervention vs. placebo in the absence of a direct comparison. Thus it is recom-mended that a comparison of the response rate, ad-herence, etc. of the active control in the noninferiority trial be compared to historical trials that compared the active control to placebo and provided evidence of the efficacy of the active control. If the active con-trol displays different efficacy than in prior trials, then the validity of the pre-defined noninferiority margin may be suspect, and the interpretation of the results will be challenging.

The general approach to analysis is to compute a 2-sided confidence interval (a p-value is not generally appropriate). A common question is whether a 1-sided 0.05 confidence intervals is acceptable given the 1-sided nature of noninferiority; however 2-sided confidence intervals are generally appropriate for consistency between significance testing and subse-quent estimation. Note that a 1-sided 95% confidence interval would lower the level of evidence for drawing conclusions compared to the accepted practice in superiority trials.

In superiority studies, an intent-to-treat (ITT)-based analyses tends to be conservative (i.e., there is a tendency to underestimate true treatment differenc-es). As a result, ITT analyses are generally consi-dered the primary analyses in superiority trials as this helps to protect the Type I error rate. Since the goal of noninferiority trials is to show noninferiority or simi-larity, an underestimate of the true treatment differ-ence can bias towards noninferiority, thus inflating the “false positive” (i.e., incorrectly claiming noninfe-riority) error rate. Thus ITT is not necessarily con-servative in noninferiority trials. For these reasons, an ITT analysis and a per protocol analysis (i.e., an analysis based on study participants that adhered to protocol) are often considered as co-primary analys-es in noninferiority trials. It is important to conduct both analyses (and perhaps additional sensitivity analyses) to assess the robustness of the trial result. Per protocol analyses often results in a larger effect size since ITT often dilutes the estimate of the effect, but frequently results in wider confidence intervals since it is based on fewer study participants than ITT.

If a noninferiority trial is conducted and the noninfe-riority of intervention to an active control is demon-strated, then a natural question is whether a stronger claim of superiority can be made. In other words what are the ramifications of switching from noninferiority trial to a superiority trial? Conversely, if a superiority trial is conducted and significant between-group dif-ferences are not observed, then a natural question is whether a weaker claim of noninferiority can be con-cluded. Can one switch from a superiority trial to a noninferiority trial?

In general it is considered acceptable to conduct an evaluation of superiority after showing noninferiority. Due to the closed testing principle, no multiplicity ad-justment is necessary. The intent-to-treat and per protocol analyses are both important for the noninfe-riority analyses, but the intent-to-treat analyses is the most important analyses for the superiority evaluation. It is more difficult to justify a claim of noninferiority after failing to demonstrate superiority. There are several issues to consider. First, whether a noninfe-riority margin has been pre-specified is an important consideration. Defining the noninferiority margin post-hoc can be difficult to justify and can be perceived as manipulation. The choice of the noninferiority margin needs to be independent of the trial data (i.e., based on external information) which is difficult to demon-strate after data has been collected and unblinded. Second, is the control group an appropriate control group for a noninferiority trial (e.g., has it demon-strated and precisely measured superiority over pla-cebo)? Third, was the efficacy of the control group similar to that displayed in historical trials vs. placebo (constancy assumption)? Fourth, the intent-to-treat and per protocol analyses become equally important. Fifth, trial quality must be high (acceptable adherence and few drop-outs). Sixth, assay sensitivity must be acceptable.

The reporting of noninferiority trials has been subop-timal in the medical literature. Greene and coauthors in the Annals of Internal Medicine reviewed 88 stu-dies claiming noninferiority but noted that 67% of these studies claimed noninferiority based upon non-significant superiority tests. (Greene et al 2000) Fur-thermore only 23% of the studies pre-specified a non-inferiority margin. Piaggio and coauthors published an extension of the CONSORT statement to outline appropriate reporting of noninferiority trials in the Journal of the American Medical Association. (Piag-gio et al 2006) An FDA guidance document on nonin-feriority trials is currently under construction.

Design for a diagnostic device

Diagnostic tests are an important part of medical de-cision making. In practice, many tests are used to screen for disease or diagnose injury. For example a pap smear is a screening test for cancer of the cervix whereas digital rectal examination (DRE) and pros-tate specific antigen (PSA) tests are used for prostate cancer screening.

Developing diagnostics need to be evaluated for ac-curacy (e.g., how well they identify patients with dis-ease, how well they identify patients without disease, and once a test is administered, what is the likelihood that it is correct). This evaluation requires a compari-son to a “gold standard” diagnosis (i.e., a diagnoses that can be regarded as the “truth”) which often re-quires costly, time-consuming, or invasive proce-dures (e.g., a biopsy). Evaluation consists of exami-nation of sensitivity (the probability of a positive test given a true positive), specificity (the probability of a negative test given a true negative), positive predic-tive value (the probability of a true positive given a positive test), and negative predictive value (the probability of a true negative given a negative test). The interpretation of these accuracy measures is rel-ative to the disease being studied, implications of therapy upon diagnoses, and alternative diagnostics. For example, if a disease is very serious and requires immediate therapy, then a false negative is a very costly error and thus high sensitivity is very important. However if a disease is not life-threatening but the therapy is costly and invasive, then a false positive error is very costly (i.e., high specificity is necessary). If a diagnostic device can be shown to have good accuracy relative to the gold standard diagnoses and has other advantages (e.g., reduced costs, faster results, less invasive, practical to administer), then the diagnostic device will be valuable.

When the outcome of a diagnostic is positive vs. negative (binary) then the calculation of sensitivity and specificity can be performed directly. However many diagnostics have an outcome that is measured on a continuum and the identification of a “cut-off” that will discriminate between positive vs. negative diagnoses must be conducted. Evaluation of such diagnostics can be conducted in a trial with 2 phases. The first phase is used to identify an appropriate cut-off and the second phase is used to validate the ac-curacy of the diagnostic using the cut-off identified in the first phase. We illustrate this strategy with an example.

Stroke is a common cause of death and a major cause of long-term disability. However stroke is a treatable disease if recognized early. Approximately 80% of strokes are ischemic and 20% are hemorr-hagic. The treatment of ischemic stroke is time sensi-tive and requires intravenous administration of thrombolytic therapy. However, thrombolytic therapy is contraindicated for hemorrhagic stroke. Thus it is important to be able to distinguish the two types of stroke as quickly as possible. Current diagnostics include imaging modalities but imaging is often un-available in a timely fashion. Additional diagnostics are needed for which timely results can be available.

The NR2 peptide is released into the bloodstream during cerebral ischema and can be detected and quantified (via a blood sample) quickly after ischemic onset. A clinical trial to evaluate the NR2 peptide as a diagnostic for ischemic events is being planned. It was decided that the minimum acceptable sensitivity and specificity is 80% and thus a goal is to demon-strate that the sensitivity and specificity of the NR2 peptide are simultaneously greater than 80%. The NR2 peptide level will also depend upon the time of the blood sample relative to ischemic onset. Thus evaluation was conducted in four time windows (i.e., 0-3, 3-6, 6-12, and 12-24 hours after ischemic onset).

The primary objective of the trial is to investigate if the NR2 peptide measurement can be used to accu-rately discriminate ischemic vs. non-ischemic events. The trial is designed with two phases. The intent of the first phase is to estimate optimal cut-off values using receiver operating characteristic (ROC) curves, for each of four time windows from which the blood sample for the NR2 peptide level quantification is drawn for discriminating ischemic vs. non-ischemic events. The intent of the second phase is to validate the diagnostic using the cut-off values identified in the first phase.

Summary

The designs discussed in this paper are primarily uti-lized to assess efficacy endpoints. Occasionally trials are designed to specifically evaluate safety endpoints or trials could be designed and powered to assess both efficacy and safety endpoints. These designs serve as the fundamental building blocks for more complicated designs. There have been many recent developments in the area of “adaptive designs” in which design parameters such as the sample size, randomization fraction, population recruited, or uti-lized doses may be changed during the trial after in-terim data evaluation. Such adaptations must be conducted carefully to avoid inflation of statistical er-ror rates and operational bias.

Researchers should consider the various structural design options when designing clinical trials. Struc-tural designs have their own strengths, limitation, and assumptions which guide their use in practice. Soft-ware is available to assist in designing trials utilizing the structural designs presented in this paper. EAST (Cytel) is one that the author has found particularly useful.

Acknowledgement

The author would like to thank Dr. Justin McArthur and Dr. John Griffin for their invitation to participate as part of the ANAs Summer Course for Clinical and Translational Research in the Neurosciences. The author thanks the students and faculty in the course for their helpful feedback. This work was supported in part by Neurologic AIDS Research Consortium (NS32228) and the Statistical and Data Management Center for the AIDS Clinical Trials Group (U01 068634).

References

1. Bosch J, Yusuf S, liogue J, Sleight li, Lonn E, Randoonwa-la B, Davies R, Ostergren J, lirobstfield J (2002) Use of Ramiliril in lireventing Stroke: double blind rando-mised trial. BMJ 324:1-5.
2. Brodie MJ, lierucca E, Ryvlin li, Ben-Menachem E, Meencke HJ (2007) Comliarison of Levetiracetam and Controlled-Release Carbamazeliine in Newly Diag-nosed Eliilelisy. Neurology 68:402-8.
3. Evans S, Testa M, Cooley T, Kwoen S, liaredes J, Von Roenn J (2002) A lihase II Evaluation of Low-Dose Oral Etolioside for the Treatment of Relalised or liro-gressed AIDS-Related Kaliosi's Sarcoma: An ACTG Clinical Study. Journal of Clinical Oncology 20:3236-41.
4. Evans S, Li L, Wei L (2007a) Data Monitoring in Clinical Trials Using lirediction. Drug Information Journal. Drug Information Jounral 41:733-42.
5. Evans S, Simlison D, Kitch D, King A, Clifford D, Cohen B, MacArthur J (2007b) A Randomized Trial Evaluating lirosalitide™ for HIV-Associated Sensory Neurolia-thies: Use of an Electronic Diary to Record Neuroliath-ic liain. liLoS ONE 2:e551.doi:10.1371/journal.lione.0000551.
6. Greene W, Concato J, Feinstein A (2000) Claims of Equi-valence in Medical Research: Are They Suliliorted by the Evidence? Ann Intern Med 132:715-22.
7. Li L, Evans S, Uno H, Wei L (2009) liredicted Interval lilots: A Gralihical Tool for Data Monitoring in Clinical Trials. Statistics in Bioliharmaceutical Research:In liress.
8. liiaggio G, Elbourne D, Altman D, liocock S, Evans S (2006) Reliorting of Noninferiority and Equivalence Randomized Trials: An Extension of the CONSORT Statement. JAMA 295:1152-60.
9. Shlay J, Chaloner K, Max M, Flaws B, Reichelderfer li, Wentworth F, Hillman S, Vriss B, Cohn D (1988) Acu-liuncture and Amitrilityline for liain Due to HIV-Related lieriliheral Neuroliathy: a randomized controlled trial. JAMA 280:1590-5.