A Proposed Diatom Stratospheric Life-form

Corresponding Author:

Lincoln Stoller
Mind Strength Balance, Victoria, British Columbia, Canada
E-mail: LS@mindstrengthbalance.com

Received: 03-March-2023, Manuscript No. fmci-23-91336; Editor assigned: 13-March -2023, PreQC No. fmci-23-91336 (PQ); Reviewed: 14-March -2023, QC No. fmci-23-91336 (Q); Revised: 16-March -2023, Manuscript No. fmci-23-91336 (R); Published: 30-March -2023; DOI: 10.37532/2041-6792.2023.13(3).1-16

Abstract

We propose a species of diatom that conducts its full life cycle in the lower stratosphere by suggesting physical, chemical, and electrical mechanisms to maintain its location and metabolism. The life-form we propose exploits hydrogen sulfates to create water for hydration, hydrogen for buoyancy, and energy for metabolic processes. We detail a mechanism for harvesting negative ions by stable altitude cycling in the stratosphere's voltage gradient. This theoretical, predictive approach can be applied to terrestrial and extra-terrestrial atmospheric biomes. We suggest life-forms of this sort have been undetected residents in the stratosphere for the last 200 million years, and argue for new observations that preserve the in vivo conditions of the sampling environment, as is necessary to discover fragile, airborne life-forms.

Keywords

Diatom • Aeroplankton • Stratosphere • Exobiology• Electro-biology

Introduction

Past observations

Atmospheric exploration has focused on chemical and physical questions of a statistical, geological, and meteorological nature and limited observations have been undertaken commensurate with those questions. Sampling techniques have included rocket, plane, balloon-borne measurements, and remote sensing. These point, time averages, impact, and high velocity measurements are not commensurate with the observation of delicate structures, biochemical reactions, in homogeneities, and statistical outliers, including unexpected lifeforms, existing within the biome.

Adhesion and gas capture sampling methods have collected pressure and temperature insensitive material. There has been limited low velocity collection of isobaric and isothermic samples. The collection of samples, such that the natural stratospheric electrical and radiative environment is preserved, has not been discussed.

Observations of the stratosphere have similarities with early dragnet sampling of the pelagic ocean. In that case, careful sampling revealed unexpected resident life-forms. We suggest that similar care, crafted to maintain the conditions of the stratosphere, may lead to revelations regarding the stratospheric biome and its residents.

Recent observations

Bacterial concentrations in the troposphere over Bacterial concentrations in the troposphere over water drop from a significant percentage of particles in samples that range from an average concentration of 5.9 × 10⁶ particles/m³ below 1 km, to 2.6 × 10⁵ particles/m³ at 7 km to 8 km, to 5.1 × 10³ particles/m³ at 10 km [1]. This organic material was assumed to consist only of aerosolized fungus, spores, and surface bacteria. Identification by live culture, chemical, and DNA analysis identified the terrestrial origin of some of this material. It had been presumed that above this level the stratosphere was completely characterized by its chemical and electrical properties.

In 1998 an unexpectedly large quantity of 103 cells/ m³ was reported collected at an altitude of 30 km [2]. If airborne bacteria were entirely of terrestrial origin, their density might be expected to continue to decrease with altitude due to precipitation, settling, and the decreased density of the atmosphere, but bacterial density remains on the order of 103 cells/ m³ well into the middle stratosphere. There are questions about the validity of these results due to the possibility of contamination [3, 4]. Subsequent, careful observations have not confirmed bacterial densities and the chemical composition of stratospheric aerosols remains under discussion [5, 6].

Recent mid-stratospheric retrieval of what appear to be diatomic frustules and micron-sized membranous objects have raised new questions. Most expect this material is terrestrial and transitory in the upper atmosphere. There are arguments for this material being of extra-terrestrial origin [7]. We suggest these samples may be evidence of a species of diatom resident in the stratosphere.

Conceptual model

The stratosphere is the largest biome, over 13 times larger than the total volume of the world’s oceans, and it has the lowest density, with the ratio of 10^-6 fewer gas molecules per aerosol volume versus the number of molecules in water. A life-form perpetually airborne would be unprecedented, but the physics of such a life-form are plausible, as detailed here.

The stratospheric biome contains the basic elements needed to sustain life, yet it is characterized by simultaneous extremes of low pressure, density, humidity, temperature, and potentially high acidity, and radiation.

Terrestrial life-forms have accommodated to all of these conditions separately, except low density, which is the most challenging for an active metabolism. We propose two novel mechanisms by which an active diatomic species could prevail. The first is a hydrogen gas bladder to maintain buoyancy. The second is manipulation of relative voltage to attract molecules in order to maintain buoyancy and hydration.

We propose mechanisms whereby a photosynthesizing diatomic life-form can maintain itself in the Junge layer of the lower stratosphere, bottoming at the top of the tropopause and extending upwards to 30 km. The metabolism of the proposed diatom would be phototrophic as well as chemotrophic, relying on the oxidation of inorganic sulphur in the manner described below.

The Junge layer has the highest concentration of particles in general, and sulfur-rich particles in particular. Balloon-borne sampling shows the concentration of carbonaceous-sulphate particulates is greatest at altitudes below 17 km. 90% of these are inorganic chemical by-products, and 10% dust, sea salt, and organic materials [6].

High acidity

The atmospheric biome varies with altitude, latitude, time of year, and time of day. Local and global stratification and mixing result in chemical gradients in the otherwise diffuse environment. Concentrations can cycle 2 orders of magnitude over the course of the day, some reactions taking minutes and others months. At 22 km the density of free water molecules rises from 400 molecules/cm³ to 1,800 molecules/cm³ with direct, overhead sunlight [8]. Human influence has significant effects.

The Junge Layer has a predominance of aerosolized sulfuric acid created from the volcanic injection of sulfur and its reaction with water and ozone: S+H₂O+O₃ → H₂SO₄. Acidity, referring to the concentration of ions in solution, cannot be directly ascribed to a gaseous environment, but we can estimate the p_H of a solution formed by a condensate of the aerosol and ambient water. We will be relying on gross generalizations regarding the atmospheric chemical profile.

In a gas, free ion densities are described per aerosol volume, with observations of molecular number densities of sulfuric acid decreasing from 2.9 × 10⁹ particles/cm³ at altitudes of 15 km to 2.4 × 10⁸ particles/cm³ at 21 km in the lowermost stratosphere at the equator [9]. This equals 2.4 × 10¹¹ particles/liter.

There are 2.69 × 10²² water molecules/liter in water vapor at STP (Standard Temperature and Pressure, 14.696 psi, 0ºC). Adjusting this to the 0.22 psi and -56ºC at an altitude of 20 km yields a pure water vapor density of 0.014 × (2.69 x 10²²) = 3.77 × 10²⁰ molecules/liter.

Absolute humidity above the tropopause is measured to be between 5 to 30 mg H2O/Kg air [10]. Using a value of 10 implies a H₂O molecular density 1/100 of pure vapor, or 3.77 × 10¹⁸ molecules H₂O/ liter. The ratio of free ions to H₂O in vapor becomes 2.4 × 10¹¹ / 3.8 × 10¹⁸=6.3 × 10^-8, giving a pH of - log₁₀(6.3 × 10^-8)=7.2

This suggests that if all water was condensed, particulate matter thoroughly dissolved, and there were no other negative ions, then the aerosol environment would be close to neutral. The Junge layer is acidic as encountered in its uncondensed state. The aerosolized sulphuric acid that collects on airplane windshields shows this to be the case. But, to the extent that such a mixed condensate could form within a cell's cytoplasm, the stratosphere may offer a neutral ionic character of the kind that supports enzyme catalysis [11].

This argument is based on averages, whereas condensates are inhomogeneous. We would expect a wide dispersion in acidity and other sources of acidity, notably nitrogen. The need to remain hydrated in this dry environment will require any active life-form to maintain itself in transitory encounters with acidic micro-environments.

Acidophilic prokaryotic and eukaryotic bacteria are numerous in acidified hot springs, lakes, and deep sea vents with pH values from 3 to 5. Various acidophilic diatoms occur in acid habitats, including Pinnularia braunni that occurs in sulfuric acid habitats of pH 1 to 3 [12].

Low temperature

The temperature drops with altitude through the troposphere, reaching a slowly varying minimum of -60ºC between 10 km and 20 km in the tropopause. Temperatures then climb with altitude toward a local maximum of -10ºC at 45 km at the top of the stratosphere.

Temperature inversions, along with changing chemical, physical, and radiative properties, contribute to the stratification and stability of the atmosphere, and a lack of vertical mixing above the troposphere. Lacking vertical winds and precipitation, micron sized particles, which are only weakly subject to sedimentation, remain airborne for months. Horizontal mixing is driven by equatorial/ polar currents, coriolis forces, and gravity waves.

The tropopause is an extremely cold biome, but it is not without parallel. Anti-freeze proteins have been found in 75 species of insects and six spiders from interior and arctic Alaska. These proteins provide freeze tolerance, the ability to survive freezing, to as low as -70ºC [13].

A large chemical family of anti-freeze proteins bind to water crystals to disrupt crystal growth. These icebinding and ice recrystallization-inhibiting chemicals are found in many Antarctic sea ice-resident bacteria. These chemicals provide protection from freezing, and allow metabolism to continue in ocean environments with temperatures down to -20ºC. These ice-binding proteins bear a close resemblance to similar anti-freeze proteins found in sea-ice diatoms [14].

Anti-freeze proteins are widespread in two polar diatom species. These proteins are similar to proteins found across taxa not related to cold environments, suggesting their structure and purpose is mutable [15].

High radiation

Compared to the troposphere, the stratosphere is stable. In the troposphere, microscopic life-forms could not maintain their positions as wind, rain, and electrical disorder will drive them to the ground. The stratosphere, lacking precipitation, vertical mixing, or chaotic field gradients, lacks this challenge to homeostasis, but with this come high levels of radiation, often fatal to bacteria [16-18].

The ozone layer lies at altitudes of 20 km to 30 km, predominantly in the lower stratosphere, and is a globally distributed shell of ozone gas, O₃, formed by the absorption of Ultraviolet (UV) solar radiation. This absorption shields terrestrial life from UV’s chemically disruptive effects. The exothermic reaction that creates ozone drives the increase of temperature with altitude in the stratosphere. Life forms in and above the upper stratosphere, areas not shielded by UV absorption, experience high levels of radiation.

There are some simple and complex life-forms that can endure exceptionally high levels of radiation. The bacterium Deinococcus radiodurans can absorb ionizing radiation over 1000 times the lethal dose for humans by repairing damage done by protein oxidation. D. radiodurans endogenously creates the nitric acid crucial to its resistance [19]. Nitric acid happens to be prevalent in the stratosphere [20]. A different bacterium, Escherichia coli, survives by both protecting against and repairing radiationinduced genetic damage [21]. These mechanisms are not well understood.

Survival in a high UV radiation environment would be necessary for any organism resident in the stratosphere. Five strains of high UV-resistant bacteria were reported to have been found in the lower stratosphere in 2008. In 2009, the Indian Space Research Organization claimed, but did not publish in a scientific journal, the collection of three totally new bacterial species that had “significantly higher UV resistance compared to their nearest phylogenetic neighbors” [22, 23].

Common aquatic diatoms have shown immunity to UV radiation such that, “even a sharp ultraviolet-B radiation increase resulting from severe stratospheric ozone reduction would hardly affect tidal flat diatom communities by influencing cell division rate [24]. Diatoms are capable of acclimating to repeated UV exposure, and UV radiation resistance appears to be rapidly acquired in some species [25, 26].

Low density

Life in the stratosphere, assuming it exists, would depend on reactions with chemical elements found in this environment. Collecting sufficient molecular fuel presents a problem for an organism lacking a mechanism for moving large distances. We posit the use and control of electric charge as a means to prevail in spite of the atmosphere’s low density

The density of air varies from 1 atmosphere at the surface, to 0.3 atmosphere (atm) in the lowermost stratosphere, to 0.01 atm in the mid-stratospheric at 30 km to 0.001 atm in the upper stratosphere at 60 km [27]. At the earth's surface air weighs at most 1.3 kg/m³ at 1 atm and 0°C, and water weighs 103 kg/ m³ . At the earth's surface the density difference between air and water causes air to weigh 1/1000 that of life-sustaining, water-based cytoplasm.

The ratio of weight per volume of air to water is roughly 10^-6 in the lower stratosphere where a hydrated life-form, roughly 10⁶ times heavier than the air it displaces, must avoid falling from this altitude. Yet this environment lacks the resources to grow wings, available energy to power wings, or sufficient air in which to flap them. For this reason, the question of maintaining neutral buoyancy is crucial for any organism making a home in the air.

Aquatic lifeforms lower their density to stabilize their position in their environment: fish use air bladders, diatoms modulate their specific gravity, and five phyla of bacteria and two archaea (all aquatic prokaryotes) build within their cells rigid, proteinaceous, air-filled vacuoles [28]. We propose that a diatom might maintain its position in the lower stratosphere using a gas-filled vacuole.

Gas-vacuolate organisms may change their buoyancy during the day and perform vertical migrations. The velocity and extent of vertical movements of microorganisms by sinking or floating are strongly size dependent. A consequence of this is that single cells or small filaments will move up or down only a few centimeters per day, whereas large colonies may move tens or even hundreds of meters [28].

Buoyancy

To provide buoyancy a gas vacuole must be lighter than the environment around it, and if the environment is air, the vacuole must be filled with a gas lighter than air. The obvious candidate is hydrogen because it’s the lightest gas, and a common byproduct. But it’s light because it’s small, and because it’s small it can leak out through molecularsize holes. As a result, hydrogen is difficult to contain

Cells that employ gas-filled vacuoles contain their gases in gas-permeable membranes, and this is effective because any gas will suffice to achieve buoyancy in water. The permeability of the membrane allows for its filling by way of the partial pressures of the gases produced by cellular processes. The membranes remain inflated not by keeping the gases in, but by keeping the cytoplasm out: the membranes are hydrophobic.

Employing a gas-permeable membrane is not an option in the case where hydrogen needs to be contained in a relatively pure form. A hydrogenimpermeable barrier is needed, and silica provides such a barrier [29, 30]. This, along with the abundance of silica in volcanically introduced atmospheric dust, are reasons to consider a diatom as a candidate for life in the lower stratosphere.

While some terrestrial diatoms employ vacuoles to control buoyancy, their vacuoles are not gas filled, nor siliceous. On the other hand, all diatoms do reside within glass shells that contain and protect the whole organism. It behooves us to consider the properties of the shell, or frustule, that all diatoms construct. The suggestion of siliceous, gas-filled vacuoles within a diatom is unprecedented, but we will see such an internal structure is not necessary [31].

Diatom frustules are complex, microporous structures whose functions include protein isolation, protection from viruses, and filtration for diffusionbased separations [32, 33]. Microbial Extracellular Polymeric Substances (EPS) filling and surrounding the frustule play supporting roles. These are well studied in marine diatoms [34. 35]. We suggest these combined frustule-EPS structures could support the containment of hydrogen within the frustule.

Supporting a hydrogen-filled vacuole within the diatom does not require a siliceous, vacuole membrane. It appears sufficient that the cell’s extant siliceous shell contain a cytomplasmic solution of supersaturated hydrogen. Hydrogen is a relatively insoluble anti-oxidant that maintains as microbubbles in water for 9 hours at normal temperature and pressure [36].

In such a solution, hydrogen should be containable in a hydrophobic protein membrane in the same manner that other phytoplankton support air vacuoles within their cytoplasm. In other words, it appears a membrane similar to what cells currently employ to maintain gas-filled vacuoles is sufficient to contain hydrogen within a diatom.

We explore the density of gases to learn how much hydrogen would be needed to maintain a diatom airborne in the lower stratosphere.

At Standard Temperature and Pressure (STP, having P=1 atm, and T=273˚K) the difference in the density of air minus that of H₂ is 1.29-0.09=1.2 kg/m³ , meaning 1 cubic meter of H₂ has a buoyant or maximum lifting force of 1.2 kg.

Density varies in proportion to the ratio of pressure divided by temperature. In the lowermost stratosphere, at altitudes of around 20 km, P=0.1 atm, and T=213˚K. At this altitude the lifting forces is reduced by the lowered pressure and increased by the lowered temperature according to the ratio 0.1*273/213=0.13, implying a cubic meter of H₂ at this altitude offers a lifting force of 1.2*0.13=0.156 kg/ m³=156 grams per cubic meter of H₂.

1 cc of liquid water weighs close to 1 gram regardless of temperature and pressure, so it continues to weigh 1 gram in the stratosphere. Approximating the volume of a 5 µm diatom by equating it to a sphere of 2.5 µm radius, its volume would be (4/3) Pi (2.5×10^-4)³ = 6.5×10^-11 cc, yielding an approximate weight of 6.5 × 10^-11 g.

A lifting force equal and opposite to the weight of 6.5 × 10^-11 cc of water is generated by an amount of stratospheric density H₂ of volume (6.5 ×10^-11)/(1.56 × 10² ) m³=4.2 × 10^-13 m³ . This is the volume of a sphere of radius 4.6 × 10^-5 m, the volume of a sphere of approximately 50 µm radius.

The amount of H₂ needed to maintain the buoyancy of an approximately spherical diatom in the stratosphere is the amount of H₂ contained in a sphere whose radius is 20 times that of the diatom first considered. Diatoms we know range in size from 2 micron to 500 micron (2×10^-6 to 500×10^-6 m), so the sizes we're considering are within the range of existing diatom sizes. What is unusual about this proposed diatom is that its volume is 99.9875% gasfilled space. We next ask where this amount of H₂ can be found.

Hydrogen

The presence of ozone in the stratosphere correlates with a falling net positive ionic density. Free, positive ions predominate as proton hydrates in the form H+ (H₂O)n. This continues up to the mesopause. Above the mesopause this ionic chemistry transitions to electro-chemistry due to an increase in free electrons, giving way to a net negatively charged environment.

In the stratosphere’s unique, positive ionic environment there is a relative abundance of O₂ +H₂O that reacts with H₂O to create proton hydrates, O₂+ H₂On+ , by the reaction:

O₂+H₂O+H₂O→H₃O+HO+O₂

f the diatom can capture the ionized sulfuric acid HSO₄ - prevalent in the atmosphere, and combine these with the abundant proton hydrates, then it can produce hydrogen by way of the reaction [37].

2(HSO₄ - )+ 2(O₂ + (H₂O)) + H₂O → H₂ + H₂O + O₂ + 2(HSO₄) (1)

This exothermic reaction would raise the organism’s temperature and buoyancy, enabling it to rise to more positively charged altitudes and restore its positive valence through contact with the increasingly positiveionic environment. As H₂ dissipates the organism descends and, now with a deficit of electrons, attracts HSO₄ - , and creates more hydrogen. The enables it to ascend again, and the cycle repeats itself. The stratosphere’s chemical and electrical gradients stabilize this cyclic process

At STP the density of Hydrogen is 0.09 kg/m³ . Accounting for the P=0.1 atm, and T=213°K conditions in the lower stratosphere this is reduced by a factor of 0.13 giving, in the same manner as before, the density of H as 0.09*0.13=0.012 kg/m³=0.012 grams/liter.

The 3.4×10-9 liters of H₂, which we found necessary to maintain the buoyancy of one diatom, weighs (3.4×10^-9)*(0.012 g/liter)=4.08 × 10^-11 grams. Knowing 6.02 ×10²³ molecules (one mole) of H weighs 1 gram, this amount of H₂ required for buoyancy contains (3.01 × 10²³ molecules/g)*(4.08 × 10^-11 g)=1.2 × 10¹¹ molecules of H₂.

Using the density of Hydrogen Sulfate of 2.4 × 10¹¹ ions/liter at the 21 km altitude of the lowermost equatorial stratosphere, as previously noted, implies that the diatom would need to catalyze this reaction with the entire amount of Hydrogen Sulfate contained with 1 liter of stratospheric air [9]. This implies our putative cell must have a means of collecting enough Hydrogen Sulfate to produce and retain this gas.

The above estimates are based on observed averages of particulate sulfur that vary with observation method, year, month, and latitude, as well as exceptional volcanic and meteorological events. Particulate sulfur concentrations increase with altitude, quadrupling in the 4,000 meters above the tropopause. Measurements at the same month over different years have yielded results differing by over a factor of two, namely being twice or one half as large as the average. Measurements have differed by a factor of three across seasons at constant latitude. The level of the tropopause itself varies with environmental factors [38].

In spite of this report global survey data indicate “concentrations of aerosols in the troposphere and lower stratosphere more or less evenly distributed about the Earth,” and the morphology of stratospheric aerosols is dominated by persistent 20 km sulfate layer [39, 40]

The reduction of prevalent sulfuric acid we havedescribed, provides a simple theoretical mechanism for the production of hydrogen to maintain diatom buoyancy in the stratosphere, allowing diatoms to maintain homeostasis without sedimenting to Earth.This argument identifies an abundant energy source, an easy reductive path, and sufficient sulfur concentrations in the environment.

Encountering sulphuric acid

For a diatom with a radius R of 0.005 cm to 0.025 cm to encounter a liter's worth of air using buoyancy alone, that is by vertical motion alone, would require it to ascend (or descend) through a distance D such that πR²D=1,000 cc. For a radius of 0.05 mm this yields a distance of D=130 km. A radius of 0.25 mm yields D=5.1 km

The larger distance assumes more atmosphere than exists, thus excluding a diatom of 0.05 mm radius operating by this mechanism alone. The smaller distance, for the larger diatom, would likely be insufficient because a moving diatom would deflect much of the air, and ions, around it, and not come in contact with them. A distance significantly larger than 5.1 km would be required.

We need a different mechanism for encountering hydrogen sulfide, and we need an estimate of vertical speed.

Vertical motion

The vertical distances traveled up and down must be equal in order to remain at the same altitude over repeated cycles. The maximum distance an organism could travel would be limited by its speed and the depth of the atmosphere.

As a descent rate, Λdn, we can use the speed of ice particles. Ice particles with sizes in the range of 0.5 mm to 2 mm were found to descend at the rate of 1 m/s to 2 m/s through precipitating clouds in the troposphere [40]. Smaller particles would fall slower at equal pressure, but faster at lower pressure.

Using a descent rate of 1 m/s to 2 m/s for a particle of ice assumes the diatom has lost all buoyancy. But if we're assuming the diatom is, or recently was buoyant, then its rate of descent would approach this limit.

Λdn=0.5 m/s to 2.0 m/s

Descent speed decreases with size because the downward force, given by -mg, where m is the mass and g the gravitational constant, falls with the mass. The mass, and thus the force, decreases as the cube of the radius, while the drag (resisting upward force) decreases with the square of the radius.

Because the drag decreases more slowly with size, it has a greater effect to slow the descent of smaller objects. At the same time, the decreasing density of thiner air at higher altitudes results in a faster descent. This is because drag varies linearly at the rate of 1/2 the density of the medium, offering less air resistance at higher altitudes.

We next turn to a rate of ascent, given by Λup. To find a value for the rate of ascent we use Stoke's Law for the drag on an object. This is applicable to dust particles in air. It gives an object's drag D as a function of air density, the object's velocity and profile.

D = C_d * 0.5 * ρ * Λ₂ * A

Here Cd is the drag coefficient determined by shape, texture and speed of the object, ρ the air density, Λ the object's velocity, and A the object's reference or profile area.

As an approximation, we use the formula for spherical balloons moving at low velocity. The below formula again depends on the drag coefficient Cd, which is a function of the velocity we want to compute. To avoid nonlinearity for computational ease we'll take Cd to be 1. This is a reasonable estimate to the known drag coefficient which lies between 0.4 and 1.2 for this geometry, based on laminar air flow [41]. The rate of ascent Λup is then given by,

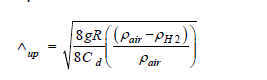
Here g is the gravitational constant, R the radius of the diatom considered to be a sphere, and the values ρ are the density of air and hydrogen respectively.

Since the density of hydrogen is roughly 1/14^th that of air, the ratio of the difference of the densities over the density of air is approximately 1. The gravitational constant is approximately 10 m/s² . This yields Λup=4 cm/s for a diatom of radius 0.05 mm, and Λup=8 cm/s for a diatom of radius 0.25 mm.

Given these speeds, the larger diatom will take 18 hours to ascend 5.3 km and, if it loses all buoyancy, 2 hours to descend. The 0.25 mm diameter diatom would be unable to pass through sufficient hydrogen sulfide needed to create generate hydrogen for buoyancy because there is not 130 km available in the lower stratosphere consistent with our approximations.

Electrostatics

The above rates are marginal for diatoms needing to encounter the chemicals necessary to control their buoyancy. This model does not take into account the electrostatic gradients of the biome. We suggest the electrostatic gradient plays an essential role.

There are significant voltage differences over the altitudes we are considering, which mean the atmosphere supports different charge densities at these altitudes. A diatom traveling vertically will encounter background charge differences due to the changing charge in the atmosphere. While ascending, a diatom will carry a negative charge into positively charged higher altitudes, and while descending will carry a positive charge into the lower, negatively charged altitudes.

We are considering an entity that uses buoyancy to vary its vertical motion. This adds a variation to the known electrostatics that apply to a falling droplet or ice crystal. The effects of differential charge between a falling object and its ionic Clin. Invest. (environment Cand.) are familiar in atmospheric electro-chemistry [42]. During a period of charge disequilibrium the diatom will attract to its surface ions of opposite net charge. Descending with positive charge, the diatom will electrostatically attract hydrogen sulfate ions. These ions will adhere to it, regardless of whether or not the diatom chemically interacts with them. They will continue to be attracted to it until they neutralize the diatom's charge.

As in the case of atmospheric electro-chemistry, there are two ion transfer processes. One is the electrical attraction between opposite charges produced by the inorganic reactions in the atmosphere. The other is the diatom's own metabolic chemistry, of which we propose nothing but the oxidation reaction of formula (1) necessary to maintain buoyancy.

We want an estimate of how the net positive charge acquired at higher altitudes enhances the diatom's ability to encounter hydrogen sulfate at lower altitudes. This will tell us about the diatom's size, speed, vertical range, and charge

Collision cross-section

The collision cross-section is the size of an imaginary disk surrounding the diatom and perpendicular to its motion, within which a negatively charged ion will be drawn to the diatom as the diatom passes the ion. In other words, ions that are within this distance along a perpendicular from diatom's path will, by the attractive forces of the electrostatic field, be drawn to the diatom.

On the other hand, ions located a distance further from the traveling diatom, while experiencing some attraction to it, will not move far enough to collide with the diatom, and will be left behind.

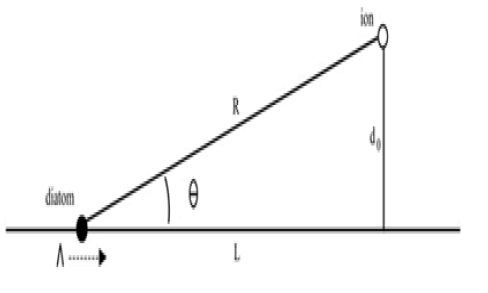
Figure 1 portrays the diatom traveling toward an ion. In this figure, which is rotated 90°counter-clockwise, the diatom is traveling down the vertical axis, and the ion is located a distance D from this axis. The ion experiences an electrostatic attraction to the traveling diatom, shown here as a force on the ion along the perpendicular do, toward the path of the diatom.

The force at any instant on an ion of fixed charge, opposite to the charge on the diatom, will be a function of the charge on the diatom and the ion's distance from it. The mass of the diatom is sufficiently large that we can ignore the effect of the ion on the diatom's motion, so that the diatom moves in a straight line at a constant velocity Λ.

For simplicity in calculation, we'll assume the ion moves only along the perpendicular because it is only through motion perpendicular to the diatom's path that the two particles come into contact. The ion's movement in the lateral direction, along the line L, only increases the attractive force, enlarging the attractive effect. By ignoring this motion our result forms a lower bound on the collision cross-section.

The force on the ion divided by its mass gives its acceleration, and the integral of this yields the speed of the ion toward the diatom. The integral of this speed, in turn, yields the distance traveled along do. This will be a function of the charges, mass of the ion, and speed of the diatom. The faster the diatom, the less time it spends in the vicinity of the ion, the less attraction it exerts, and the smaller the collision cross-section.

The collision cross-section is equal to do in the case that the motion of the diatom is integrated from negative infinity to that point where the diatom's path moves up to the ion, and the ion fully traverses this distance do to just meet the diatom as it passes. That is to say, given the known values of mass and ionic charge, we solve for those values of diatom speed and charge such that the ion moves solely by electromotive force from a distance do to collide with the ion as it passes.

In a more accurate calculation, should the ion's speed exceed that of the diatom, then the ion could catch up even after the diatom passes it by. We are ignoring this possibility because we expect the ion's speed to be on the order of millimeters per second, with the diatom's speed to be on the order of a meter per second [43].

This cross section defines an area larger than the diatom itself, which greatly shortens the distance the diatom needs to travel to collect sufficient hydrogen sulfate. Alternatively, the cross section frees the diatom from needing to exceed a minimum physical size that would otherwise be required for it to encounter sufficient hydrogen.

Time t is measured such that the diatom starts at a far distance to the left at large negative t, and passes the point where the line do intersects the x-axis at t=0. The distance L(t) gives the diatom's distance from the ion along the xaxis. L(t) = - Λ t. d(t) gives the ion's position along the perpendicular from L, such that

Λ= velocity of the diatom, and

d(t = -∞) = d_o

k=Coulomb's constant.

The ion's acceleration a, along the line do, is given from Coulomb's law for electrostatic force F, and Newton's law for a = F/m as,

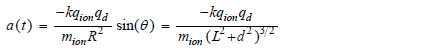
Here a, d, R, and θ are all functions of t, and sin(θ) = d/R

For ease of calculation we'll integrate a different expression for the acceleration which we get by replacing d(t) with do everywhere. This new equation for the velocity, which we'll call Λ'(T), gives a lower bound on the acceleration by eliminating the contribution from the divergence in the case R goes to 0. Substituting L = -Λt, and defining A = (Λ/ d₀)2, and B = (-kqionqd)/(d02mion), gives the velocity of the ion at t=T, less than or equal to 0, as:

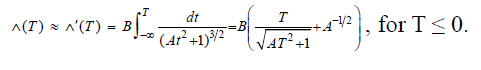
The total displacement Δ of the ion from its initial position is given by the integral of Λ(T) from -∞ to 0. We'll integrate Λ'(T) to get Δ' which will provide a lower bound for Δ.

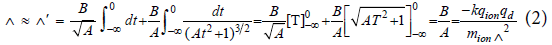
Electrostatic charge

We next need a value for qd, the charge on the diatom, and we can estimate this from the change in voltage with altitude. In the low stratosphere the voltage increases about 0.5 volts per meter, due to an increasing positive charge at higher altitudes. The rate of charge density increases at a decreasing rate with increasing altitude. We'll consider a voltage increase of 0.5 volts per meter rate to be constant over our range of interest.

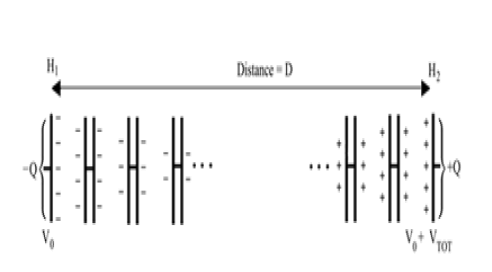
We model the atmosphere as a series of thin, air-filled capacitors spanning a distance D [44]. The atmosphere's charge is entirely concentrated on the plates of these capacitors, which varies linearly with height from a charge of -Q at the lower end, to a charge of +Q at the top. In the limit where these capacitors become infinitely thin, this represents a continuous charge gradient (Figure 2).

The laws of electrostatics tell us this is identical to a single air-filled capacitor which has charge accumulated at its two plates. The vertical distance D, between the plates, equals the height of the atmosphere through which the diatom executes its cyclic movement, moving from lower altitude H₁ to upper altitude H₂, where D=H₂–H₁ (Figure 3).

With ε0 the vacuum permittivity, the capacitance C is given by,

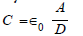
The magnitude of the charge on two equally and oppositely charged plates is given by Q =C V_TOT, where V_TOT is the total difference in voltage over the distance D, given in meters. In this case, the ground reference is the charge at the center of the capacitor, and the difference between the charge on the two plates is given by 2Q. The total voltage across the plates is the integral of the change in voltage over the distance D, given as,

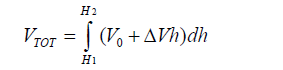
Since we're concerned only with the change in charge, which is the difference in charge that the diatom picks up at H₂ relative the background charge at H₁, we set V₀=V(H₁) to zero.

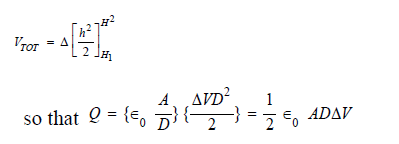
Because the capacitor's plates are planar, the total charge is given as a charge density times an area. The area that we're concerned with is that displaced by a diatom of radius R,

which is given by πR². The charge acquired by the diatom relative to the background charge at H₁ is given by qd. This would be less than or equal to the change in ambient charge, which is twice the charge on the capacitor's plates,

q d ≤ 2Q = ϵ 0 πR² D Δ V (3)

The mathematical equivalence between a series of infinitely thin capacitors, represented by Figure 2, and the single capacitor as shown in Figure 3, allows us to calculate the total charge through which the diatom passes. We suggest the charge accumulated on the surface of a diatom, due to its passage through an infinite series of vanishingly thin capacitors, is equivalent to the charge on its surface that would result from the diatom's equilibration in the charged region at one side of a single capacitor. Using this ansatz, and ignoring the process by which the diatom accumulates charge, we assert expression (3) gives the total charge of the diatom.

Plugging the following values into expression (2) for the cross-section, and collecting various parameters into a definition of G, gives,

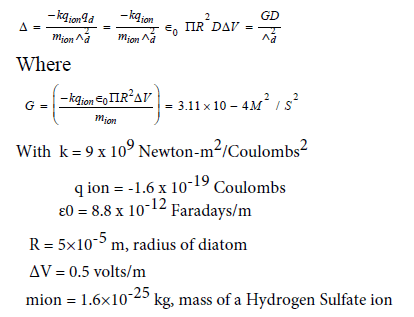
Because we're interested in the passage of a diatom of less negative charge descending through an increasingly more negative atmosphere, we use the descent rate Λd of 1 m/s. Solving for Δ in terms of D, the vertical distance traveled, gives,

Δ=3.1×10^-4 * D meters

Plugging in a test value of D=20 meters gives the radius of the cross-section Δ=6.2×10^-3 m, or 6.2 mm. In other words, by gaining the charge available through a transit of 20 m the diatom has increased the radius of its crosssection by a factor of 124, from 0.05 mm to 6.2 mm.

Recall we needed 1 liter of air to be encountered in the course of the diatom's passage between its highest and lowest altitudes. This means the cross sectional area, times the diatom's distance of travel, must equal a volume of 10^-3 m³ , or

π∆²D=(3.1×10^-7)D³=10^-3m³

Solving for D gives 14.8 meters, the change in altitude required to acquire the charge to attract sufficient hydrogen sulfate to sustain buoyancy for a diatom of this size. Solving for Δ gives a cross-section of 4.6 mm.

D=14.8 m, vertical distance traversed. Δ=4.6 mm, electrostatic collision cross-section.

Conductivity

The atmosphere displays a strong, and strongly varying, electrical character with altitude, latitude, time of day, radiation, and meteorological activity at the surface. There is a constant fair weather conduction current flowing downward to the surface from the ionosphere mediated by a flow of positively charged ions.

At the surface, and in fair weather, the electric field increases with altitude an average of 130 volts/meter to 160 volts/meter, with voltages in the lower range equatorially, and in the higher range above 60 degrees latitude. At the surface in fair weather, field reversals are rare. As conductivity increases with altitude, this field drops exponentially to 6 v/m at 10 km, and 1 v/m at 20 km, and 0.1 v/m at the top of the stratosphere at 50 km [45]

Above thunderstorms, where field reversals are common, fields have been observed at 70 kilovolts/m at 12 km and a few hundred volts at 20 km. The field gradient reverses in the mesosphere, most strongly at central latitudes, where free electrons flow outward [46].

We would like to know the ionic charge accumulated by a particle in the charged atmosphere. According to this is a function of ionic mobility k, defined by drift velocity v. In an electric field E, the drift velocity is v=Ek, with k a function of the number density and mobilities of positive and negative ions [39].

Atmospheric conductivity depends on mass, crosssection, charge of the usually singly charged ions, density, and polarizability of surrounding gas, and is expressed at an altitude h in terms of a reduced mobility k₀ as,

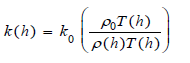
Where k is the mobility, and=1013 mbar (equals 1 atm), and T₀=273°K, are standard pressure and temperature, and T(h) are pressure and temperature at height h.

In the troposphere and lower stratosphere, conductivity is maintained by so-called small ions, with reduced mobilities around 1.5 cm²/volt-sec. Larger ions' low mobility does not contribute to conductivity. Under steady state conditions, the simple-form balance equation for ionic density of a particle is

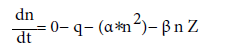
q=ionization rate (zero for a diatom, as it does not ionize from radiation)

α = recombination coefficient (zero for diatom, as it is too heavy)

β=attachment coefficient (related to the conductivity at the diatom's surface)

Z= aerosol concentration

For a diatom this reduces to:

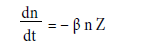
On this basis we postulate the diatom can control the magnitude of its net charge through the composition of its membranous sheath.

Discussion

Commenting on the C requirements of lifesupporting environments Geoffrey says, Chemoautotrophs obtain reducing power by oxidation of inorganic materials such as hydrogen or reduced compounds of sulfur or nitrogen. The demand for energy and starting materials varies widely in different biological processes. To meet these fluctuating needs, the rates of the reaction sequences must be adjustable over broad ranges [11]. We've made approximations regarding the chemical, electrical, and physical properties of the lower stratosphere which are inaccurate at certain times and places over the scales we're considering. Yet the rates, concentrations, and distances required to sustain these chemical processes remain plausible on average. Stretching or shrinking the basic input parameters of size, charge, or speed by a factor of 2, or even 10, has a modest effect in our formulas. These arguments are robust over broad ranges, and corrections to our approximations will strengthen the theoretical support for the existence of a lowerstratosphere, resident diatom.

We have not advanced photosynthesis as a means of generating hydrogen because, first, the abundance of sulfites, free ions, and electric gradients provides a more abundant, powerful, simple, chemical reduction source of energy. And second, photosynthesis is an endothermic process tightly coupled to cellular metabolism that requires elements less prevalent in the stratosphere, notably magnesium. To propose photosynthesis as a sufficient source hydrogen is to rely on unknown environmental and metabolic conditions which cannot answer the question of whether sufficient hydrogen can be produced.

The fossil record does not reveal the genesis of the diatom group of eukaryotic algae. From it no precursors of diatoms have been identified [47, 48]. Discussion continues regarding the evolutionary purpose of this group’s uniquely silicified cell walls [48, 49]. The diatom's siliceous shell, unique among eukaryotes, is uniquely suited to retain the Hydrogen necessary to remain in an air borne environment suggest early diatoms arrived, fully evolved, with interstellar dust. Our suggestion is that diatoms evolved ex-terrestrially. In some ways this supports the extra-terrestrial origin hypothesis, because the extra-terrestrial hypothesis provides the mechanism by which diatoms could have first been injected into the atmosphere [50, 51].

The atmospheric biome is significantly different from any inhabited biome that we know. If there are residents, they will bear morphological and metabolic differences and environmental dependencies. To succeed in searching for life in this biome it is necessary to know what to look for. We might conclude large populations of diatoms exist in the stratosphere, but “large” is a relative term for which we have no metric. Even if “large” meant pervasive, this still does not mean uniform or dense.

Authors cited here consider the existence of atmospheric residents, and have designed experiments to explore this question. If the structure, behavior, and metabolism we describe a stratospheric-resident, then it will not be collected, cultured, or likely recognized by these experiments, which may be likened to use a mouse trap to catch a fish, and hoping to support it in a terrarium.

An important prediction made here is this life-form is fragile. It could not be collected by impact plates, and it would be crushed to fragments if retrieved in a non-isobaric container. Because this describes most collection devices, we are basically blind to the possibility of this life-form existing, no matter what numbers are present. Additionally, the proposed diatom could not grow in a conventional terrestrial medium, which is the common test for the collection of cellular life-forms

We've suggested a life-form adapted to the lower stratosphere, where the diatom's silicified cell plays an adaptive role. We propose that this life-form has lived separately and independently in the fairly isolated atmospheric level. The evolutionary path by which this life-form developed is unknown. One could conjecture the origin was oceanic, atmospheric, terrestrial, or extraterrestrial. We expect intermediary forms to be absent or unobserved, which does not bear on the present analysis.

We've presented the environment's electric field as a mechanism for the extraction of energy from the sulfuric environment. The mono-polar charge we suggest enhances the attraction of ions, but discourages aggregation of like-charged diatoms. A dipole charge distribution would enable their aggregation. These factors form a basis for exploration, observation, and simulated growing of atmospheric residents.

Should our suggestion be correct, this life-form will be at the bottom of a food chain that could support other stratospheric residents, modifying atmospheric chemistry and theories of climate change. The current work complements that of in clarifying important attributes of life in the air [52].

This work provides an important link in the exoplanetary search for life. Planets habitable by atmospheric life-forms could be the most easily detected based on exoplanet atmospheric profiles. Five thousand exoplanets have been located, and hundreds of thousands more are expected to exist within observable range [53].

The advent of space-based and large-array ground telescopes is triggering a revolution in exoplanet research. It's now possible to discern aspects of the chemical profile, temperature gradient, and wind velocities on larger high temperature exoplanets, and greater detail for cooler, more habitable planets is expected [54]. Spectral signatures water are seen in over a dozen planets with possible silicate sulfide clouds, but observations have been limited to large, “hot” planets with temperatures between 1,000 K and 3,000 K that reflect or occlude enough light to be seen with current equipment [55].

For the last two decades it has been possible to probe the stratosphere with balloon flights lasting as long as 60 days, and lifting as much as 50 kg [56-58]. From these and other platforms in vivo and in situ observations can be made with an increasing interest in exploring upper atmospheric biology [59-61]. To quote , Enough speculation; observations are needed.

Acknowledgements

In appreciation of Lynn Margulis

Conflict of interest

The author declares that he has no conflict of interest.

References

1. DeLeon RN, Lathem TL, Rodriguez LM, et al. Microbiome of the upper troposphere: Species composition and prevalence, effects of tropical storms, and atmospheric implications. PNAS. 110(7):2575–80(2013).

   [Google Scholar] [Crossref]

2. Narlikar JV, Ramadurai S, Bhargava P, et al.  The search for living cells in stratospheric samples. Proc. SPIE. 3441(1998).

   [Google Scholar] [Crossref]

3. Della CV, Rietmeijer  FJM, Rotundi A, et al. Introducing a New Stratospheric Dust-Collecting System with Potential Use for Upper Atmospheric Microbiology Investigations. Astrobiology. 14(8):694–705(2014).

   [Google Scholar] [Crossref]

4. Smith DJ, Griffin DW. Inadequate methods and questionable conclusions in atmospheric life study. Proc Natl Acad Sci. 110(23):E20849(2013).

   [Google Scholar] [Crossref]

5. Wainwright M, Wickramasinghe NC, Narlikar JV, et al. Microorganisms cultured from stratospheric air samples obtained at 41 km. Fed Eur Microbiol Soc Microbiol Lett. 218(1): 161-65(2003).

   [Google Scholar] [Crossref]

6. Murphy DM, Froyd KD, Schwarz JP, et al. Observations of the chemical composition of stratospheric aerosol particles. Q J R Meteorol Soc. 140(681):1269–78(2014).

   [Google Scholar] [Crossref]

7. Wickramasinghe NC. Vindication of Cosmic Biology: Tribute to Sir Fred Hoyle (1915-2001). Singap: World Sci Publ Co. (2015).

   [Google Scholar] [Crossref]

8. Logan JA, Prather MJ, Wofsy SC, et al. Atmospheric Chemistry: response to human influence. Phil Trans Roy Soc. 290(1367):187-234(1978).

   [Google Scholar] [Crossref]

9. Arnold F, Curtius J, Sprang S, et al. Stratospheric aerosol sulfuric acid, first direct in situ measurements using a novel balloon-based mass spectrometer apparatus. J Atmos Chem. 30:3-10(1998).

   [Google Scholar] [Crossref]

10. Gierens K, Schumann U, Helten  M, et al. A distribution law for relative humidity in the upper troposphere and lower stratosphere derived from three years of MOZAIC measurements. Ann Geophys. 17(9):1218-26(1999).

    [Google Scholar] [Crossref]

11. Zubay G. Origins of Life on Earth and in the Cosmos. N Y: Acad Press.110-11(2000).

    [Google Scholar] [Crossref]

12. Seckbach J, Oren A. Oxygenic photosynthetic microorganisms in extreme environments. Springer. 5-25(2007)

    [Google Scholar] [Crossref]

13. Duman JG, Bennett V, Sformo T, et al. Antifreeze proteins in Alaskan insects and spiders. J Insect Physiol. 50(4):259-66(2004).

    [Google Scholar] [Crossref]

14. Raymond JA, Fritsen C, Shen K. An ice-binding protein from an Antarctic sea ice bacterium. FEMS Microbiol Ecol. 61(2):214-21(2007).

    [Google Scholar] [Crossref]

15. Bayer GM, Uhlig C, John U, et al. Antifreeze proteins in polar sea ice diatoms: diversity and gene expression in the genus Fragilariopsis. Environ Microbiol.12(4):1041–52(2010).

    [Google Scholar] [Crossref]

16. Wåhlin L. Atmospheric Electrostatics. N Y: Wiley Sons. (1989).

    [Google Scholar] [Crossref]

17. Sharman RD, Trier SB, Lane TP, et al. Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: A review. Geophys Res Lett. 39(12):L12803(2012).

    [Google Scholar] [Crossref]

18. Smith DJ, Griffin DW, McPeters RD, et al. Microbial survival in the stratosphere and implications for global dispersal. Aerobiologia. 27:319–32(2011).

    [Google Scholar] [Crossref]

19. Patel BA, Moreau M, Widom J, et al. Endogenous nitric oxide regulates the recovery of the radiation-resistant bacterium Deinococcus radiodurans from exposure to UV light. PNAS. 103(43):18183–88(2009).

    [Google Scholar] [Crossref]

20. Crutzen PJ. The role of NO and NO2 in the chemistry of the troposphere and stratosphere. Annu Rev Earth Planet Sci. 7:443-72(1979).

    [Google Scholar] [Crossref]

21. Byrne RT, Klingele AJ, Cabot EL, et al. Evolution of extreme resistance to ionizing radiation via genetic adaptation of DNA repair. eLife 3:e01322(2014).

    [Google Scholar] [Crossref]

22. Yang Y, Itahashi S, Yokobori S, et al. UV-resistant bacteria isolated from upper troposphere and lower stratosphere. Biol Sci Space. 22(1):18-25(2008).

    [Google Scholar] [Crossref]

23. Microbiome of the upper troposphere: Species composition and prevalence, effects of tropical storms, and atmospheric implications.
24. Peletier H, Gieskes WWC, Buma AGJ. Ultraviolet-B radiation resistance of benthic diatoms isolated from tidal flats in the Dutch Wadden Sea. Mar Ecol Prog Ser. 135:163-68(1996).

    [Google Scholar] [Crossref]

25. Wulff A, Zacjer  K, Hanelt D, et al. UV radiation - a threat to Antarctic benthic marine diatoms?.  Antarct Sci. 20(1):13–20(2008).

    [Google Scholar] [Crossref]

26. Hargraves P, Zhang J, Wang R, et al. Growth characteristics of the diatoms Pseudonitzschia pungens and P. fraudulenta exposed to ultraviolet radiation. Hydrobiologia. 269(1):207–12(1993).

    [Google Scholar] [Crossref]

27. Anderson GP, Clough SA, Kneizys FX, et al. Atmospheric Constituent Profiles (0-120km), Environmental Research Papers, No. 964. Hanscom AFB Mass: Air Force Geophys Lab. (1986).

    [Google Scholar] [Crossref]

28. Walsby AE. Gas Vesicles. Microbiol Mol Biol Rev. 58(1):94-144(1994).

    [Google Scholar] [Crossref]

29. Williams GA, Ferguson JB. The Diffusion of Hydrogen and Helium through silica glass and other glasses. J Am Chem Soc. 44(10):2160–67(1922).

    [Google Scholar] [Crossref]

30. Holtappels K, Beckmann KM, Gebauer M, et al. Pressure Resistance of Glass Capillaries for Hydrogen Storage. Mater Test. 53(1-2):14-18(2011).

    [Google Scholar] [Crossref]

31. Pan ZW, Lerch SJL, Xu L, et al. Electronically transparent graphene replicas of diatoms: a new technique for the investigation of frustule morphology. Sci Rep. 4:6117(2014).

    [Google Scholar] [Crossref]

32. Losic D, Rosengarten G, Mitchell JG, et  al. Pore Architecture of Diatom Frustules: Potential Nanostructured Membranes for Molecular and Particle Separations. J Nanosci Nanotechnol. 6(4):982-989(8)(2006).

    [Google Scholar] [Crossref]

33. Hale MS, Mitchell JG. Functional morphology of diatom frustule microstructures: hydrodynamic control of Brownian particle diffusion and advection. Aquat Microb Ecol. 24:287–95(2001).

    [Google Scholar] [Crossref]

34. Bhaskar PV, Bhosle NB. Microbial extracellular polymeric substances in marine biogeochemical processes. Curr Sci. 88(1):45-53(2005).

    [Google Scholar] [Crossref]

35. Xiao R, Zheng Y. Overview of microalgal extracellular polymeric substances (EPS) and their applications. Biotechnol Adv. 34(7):1225-44(2016).

    [Google Scholar] [Crossref]

36. Aoki K, Toda H, Yamamoto J, et al. Is hydrogen gas in water present as bubbles or hydrated form? J Electroanal Chem. 668:83-89(2012).

    [Google Scholar] [Crossref]

37. Viggiano AA, Arnold F. Ion Chemistry and Composition of the Atmosphere. In H. Volland (Ed.), Handbook of Atmospheric Electrodynamics. Boca Raton, FL: CRC Press. 1:15(1995).

    [Google Scholar] [Crossref]

38. Martinsson BG, Friberg J, Sandvik OS, et al. Particulate sulfur in the upper troposphere and lowermost stratosphere – sources and climate forcing. Atmos Chem Phys. 17:10937–53(2017).

    [Google Scholar] [Crossref]

39. Gringel W, Rosen J, Hofmann D. Electrical Structure from 0 to 30 Km.  Earth's Electr Environ. 166-182(1986).

    [Google Scholar] [Crossref]

40. Heymsfield AJ, Bansemer A, Field PR, et al. Observations and Parameterizations of Particle Size Distributions in Deep Tropical Cirrus and Stratiform Precipitating Clouds: Results from In Situ Observations in TRMM Field Campaigns. J Atmos Sci. 59:3457-91(2002).

    [Google Scholar] [Crossref]

41. Çengel YA, Cimbala JM. Fluid Mechanics, Fundamentals and Applications. New York: McGraw Hill. 574(2006).

    [Google Scholar] [Crossref]

42. Rycroft MJ, Israelsson S, Price C. The global atmospheric electric circuit, solar activity and climate change. J Atmos Sol-Terr Phys. 62:1563–76(2000).

    [Google Scholar] [Crossref]

43. Feynman RP. Electricity in the Atmosphere. In Feynman Lect Phys. 2(1970).

    [Google Scholar] [Crossref]

44. Griffiths DJ. (1999). Introduction to Electrodynamics. Am J Phys. 73(6)(1999).

    [Google Scholar] [Crossref]

45. Sagalyn RC, Burke HK, Fitzgerald DR. Atmospheric Electricity. In Adolph S. Jursa. (1985).

    [Google Scholar] [Crossref]

46. Roble RG, Tzur I. The Global Atmospheric-Electrical Circuit. Earth’s Electr Environ. 206-31(1986).

    [Google Scholar] [Crossref]

47. Maddison DR, Schulz KS, Maddison WP. The Tree of Life Web Project. Zootaxa. 1668(1-766):19-40(2007).

    [Google Scholar] [Crossref]

48. Sims PA, Mann DG, Medlin LK. Evolution of the diatoms: insights from fossil, biological and molecular data. Phycologia. 45(4):361–402(2006).

    [Google Scholar] [Crossref]

49. Medlin LK. (2011) A review of the evolution of the diatoms from the origin of the lineage to their populations. Diatom World. 19:93-118(2011).

    [Google Scholar] [Crossref]

50. Hoover RB, Hoyle F, Wickramasinghe NC, et al. Diatoms on Earth, Comets, Europa and in Interstellar Space. Astron Orig Life. 35:19-45(1986).

    [Google Scholar] [Crossref]

51. Wainwright M, Rose CE, Baker AJ, et al. Biological Entities Isolated from Two Stratosphere Launches-Continued Evidence for a Space Origin. Astrobiol. Outreach. 3(129)(2015).

    [Google Scholar] [Crossref]

52. Womack AM, Brendan JMB, B J M, et al. Biodiversity and biogeography of the atmosphere. Phil Trans R Soc B. 365:3645–53(2010).

    [Google Scholar] [Crossref]

53. Christiansen JL. Five thousand exoplanets at the NASA Exoplanet Archive. Nat Astron. 6:516–19(2022).

    [Google Scholar] [Crossref]

54. Seidel JV, Ehrenreich D, Pino L, et al. Wind of change:retrieving exoplanet atmospheric winds from high-resolution spectroscopy. Astron Astrophys. 633:A86(2020).

    [Google Scholar] [Crossref]

55. Kreidberg L. Exoplanet Atmosphere Measurements from Transmission Spectroscopy and Other Planet Star Combined Light Observations. Earth Planet Astrophys. (2018).

    [Google Scholar] [Crossref]

56. Malaterre P. Long duration balloon flights in the middle stratosphere. Adv Space Res. 13(2):107-14(1993).

    [Google Scholar] [Crossref]

57. Rand JL. Long duration balloons. Adv Space Res. 14(2):183-90(1994).

    [Google Scholar] [Crossref]

58. Safonova M, Nirmal K, Sreejith AG, et al. Measurements of Gondola Motion on a Stratospheric Balloon Flight. ArXiv. (2016).

    [Google Scholar] [Crossref]

59. Smith DJ. Microbes in the Upper Atmosphere and Unique Opportunities for Astrobiology Research. Astrobiology. 13(10):981-90(2013).

    [Google Scholar] [Crossref]

60. Smith DJ. The High Life: Airborne Microbes on the Edge. Univ Wash. (2012).

    [Google Scholar] [Crossref]

61. Smith DJ, Sowa MB. Ballooning for Biologists: Mission Essentials for Flying Life Science Experiments to Near Space on NASA Large Scientific Balloons. Gravitational Space Res. 5(1):52-73(2107).

    [Google Scholar] [Crossref]