Review Article - Interventional Cardiology (2021) Volume 13, Issue 4
Golden ratio and fractals in mitral valve geometry: Potential implications for valve imaging assessment
- Corresponding Author:
- Luca Deorsola
Pediatric Cardiac Surgery,
Regina Margherita Children’s Hospital,
Turin,
Italy,
E-mail: deorsola@libero.it
Received date: June 11, 2021; Accepted date: June 25, 2021; Published date: July 02, 2021
Abstract
Nowadays, the procedure of choice to manage a diseased Mitral Valve is represented by conservative treatment. Geometrical references are fundamental to perform a correct evaluation on a diseased valve, to plan the best repair strategy and to assess its results, both during the procedure and at follow-up. In the last decades, the number and the precision of these references have widely grown, due to a significant amount of research, as well as to a rapid empowering of imaging software and devices. Therefore, the routine measurements now obtainable from the different imaging techniques allow an extensive and deep spatial evaluation of valve geometry. Similarly, both repair techniques and devices have undergone a consistent improvement in the last years, adding to traditional surgery a wide series of percutaneous and hybrid procedures. In this scenario, an accurate geometrical analysis of the whole valve is actually mandatory, particularly when a hybrid or percutaneous approach is chosen and imaging is the only available eye. In two recently published papers, we hypothesized that the healthy Mitral Valve could have a geometrical structure based on Golden Ratio, Fibonacci Series and Fractals, a scalar 3D model where all components are related one another by defined proportions and fit together like the pieces of a puzzle. Such a model, with the use of very simple calculations, can describe every geometrical reference of the Mitral Valve and seems to predict their expected normal values.
After a brief summary about the results of our previous research, we have reviewed literature concerning the most common geometrical references retrievable from imaging and currently employed to evaluate the Mitral Valve. Published data and normality ranges have been compared with the values obtained from the 3D model, showing how it seems to produce the same results and give them a logical interpretation.
Keywords
Mitral valve • Golden ratio • Fibonacci series • Fractals • Interventional procedures
Introduction
Conservative treatment is nowadays the routine choice to approach a diseased Mitral Valve. Originally based on conventional on-pump surgery, in the last years it has been integrated by several either off-pump or trans-catheter procedures. Particularly, this new kind of interventions is rapidly growing, due to the ever better knowledge of valve anatomy and function, as well as to the impressive improvement occurred in the last years to medical devices, software, materials and engineering techniques. When planning mitral repair, a deep and extremely accurate valve analysis is mandatory, particularly when an interventional technique is chosen, where a direct anatomical evaluation is impossible. Imaging techniques, mainly echocardiography, are the best available tool for assessing both the structure and the function of the Mitral Valve.
Evaluating valve disease, planning a repair strategy, monitoring the effects, during of immediately after the procedure, and carrying out the follow-up are the routine taken steps. For this purpose, the most important information obtainable from imaging techniques consists of a huge amount of measurements, which allow us to describe and quantify with precision structure and function of the valve. In the last decades, medical imaging devices, computers and software power have undergone an extremely fast and impressive improvement, making this amount of measurements ever bigger and more accurate.
In two recent studies we focused on the Coaptation Triangle and on the Mitral Scallops, describing how their geometrical structure, in normal valves, could be based on Golden Proportion, Fractals and Fibonacci Series [1,2].
This review summarizes the geometrical 3D model of the Mitral Valve partially presented in our previous research and compares its geometrical references with the corresponding values described in literature and routinely employed when planning, performing and evaluating a conservative valve treatment. The aim is to show how this 3D model describes the whole valve geometry and how, employing very easy calculations only, it seems to produce the same results published in literature and to allow a logical explanation or normality ranges.
Proportional Geometry
Golden ratio
The term “Golden Section”, “Golden Proportion” or “Golden Ratio” refers to a way of dividing a segment into two different parts, so that the shorter is to the longer as the longer is to the whole segment. This ratio has an irrational value known as “Golden Number” and usually rounded to 0.618 or 1.618, depending on whether it is obtained dividing the shorter by the longer part or vice versa.
The knowledge of this ratio is not datable. It was documented for the first time by Euclid and Pythagoras in the 4th century B.C [3], and deeply analyzed by the mathematician Luca Pacioli during the Renaissance [4]. However, the most important fact is that it has been observed in a consistent amount of natural settings, such as physics, botanics, biology and even human anatomy and physiology [5-12]. Recently, it has also been observed in the human heart, even if available studies are limited to a gross description only [13- 16]. Nowadays, the Golden Number is an important mathematical constant, represented by the Greek letter Φ (phi). Particularly, the lower case (ï»¿Φ ï»¿) stands for 0.618…, while the upper case (Φ) for 1.618…. Moreover, this is the only known value to show a couple of important and unique mathematical characteristics: 1.618 squared is equal to itself plus 1 (1.618²=1.618+1=2.618), while 1 divided by 1.618 gives 0.618.
Fibonacci series
The Fibonacci Series is a famous sequence of numbers, named after its inventor: The mathematician Leonardo Fibonacci. It is an infinite progression of integer values, starting from 0 and growing up with a simple mathematical rule: Each value is the sum of the two previous ones. Thus, after 0 and 1, it goes on with 1, 2, 3, 5, 8, 13, 21, etc. Fibonacci published this series around 1200 A.D., in his “Liber Abbaci” (Book of Calculus), as an example to show the positional numbering system he had learnt from the Arabic people of Northern Africa. However, in time, it became ever more evident that such a numerical pattern is one of the strongest rules of Nature, mainly when dealing with growth and reproduction processes [15]. Moreover, around 1600, the astronomer Johannes Kepler realized there is a strong connection between Fibonacci Series and Golden Ratio: The ratio between two consecutive values is extremely close to the Golden Number and the more we go down the sequence the closer it gets [17].
Fractals
The term “Fractal” indicates a specific geometrical structure based on self-recurrence and self-nidification. At first sight, fractal objects appear hardly defined and chaotic, not complying with conventional geometry. However, at a careful look, it is evident that they can be broken down into smaller pieces, different in dimension, but identical in shape: The same of the original object. In turn, these pieces can be broken down into ever smaller parts, with the same result, and so on infinitely. Fractals are a quite early discovery, made between the 70s and 80s by the Polish mathematician Benoit Mandelbrot, who defined the inner structure of these elements as “self-similar” [18]. Again, Fractal objects are another basic rule in Nature and fractal growth is the most diffused pattern in the universe. Mountains, trees, leaves, river deltas are only a few examples [19-21]. Moreover, fractal growth is often based on Golden Ratio, since it allows the most efficient space arrangement, avoiding both overlaps and empty areas at the same time [22].
Coaptation triangle
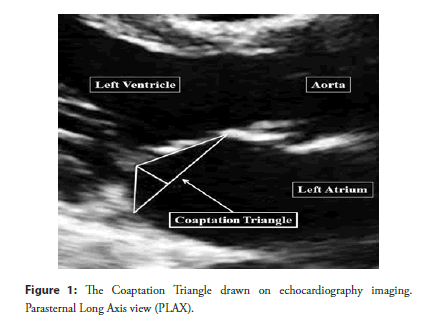
The “Coaptation Triangle” or “Tenting Area”, identifiable in Parasternal Long Axis view during systole, is an upside-down triangle, where the base is the Mitral Anteroposterior Diameter (APD) and the two sides are the Anterior Scallop and the P2 Scallop (Figure 1). Many useful measurements can be retrieved from this triangle, which are nowadays routinely employed to analyze valve geometry [23-27].
Figure 1: The Coaptation Triangle drawn on echocardiography imaging. Parasternal Long Axis view (PLAX).
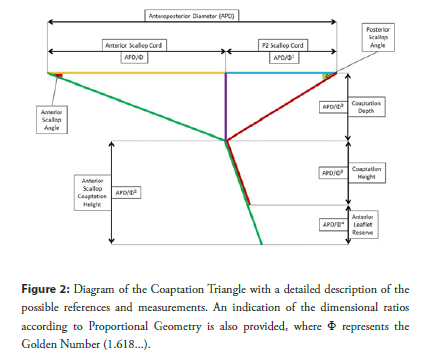
In a previous research, we found that Golden Proportion looks to define the geometrical structure of the Coaptation Triangle in the healthy mitral valve [1]. This peculiar scalar structure follows a fractal pattern and involves the Anteroposterior Diameter, the Anterior Scallop and P2 Scallop Cords, as well as the Coaptation Depth. A detailed description is presented in Figure 2.
Mitral scallops
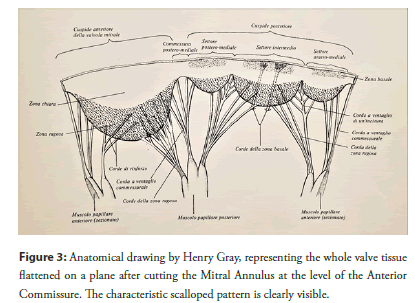
The Mitral Valve is commonly considered to have two Leaflets: One anterior and one posterior, the latter divided into three Scallops (P1, P2 and P3). However, all anatomical studies state there is only one leaflet, a continuous veil of tissue running along the Annulus [28-32]. This veil is divided into four Scallops, with the same shape but different dimensions (Figure 3).
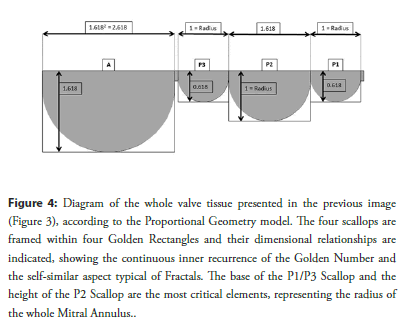
In our last research, we found that also the Scallop geometry looks to be based on Golden Proportion and have a fractal structure [2]. Again, the Scallops appear to show a fractal and scalar pattern based on Golden Ratio, which determines both their aspect and their dimensional relationships. Details are shown in Figure 4.
Figure 4: Diagram of the whole valve tissue presented in the previous image (Figure 3), according to the Proportional Geometry model. The four scallops are framed within four Golden Rectangles and their dimensional relationships are indicated, showing the continuous inner recurrence of the Golden Number and the self-similar aspect typical of Fractals. The base of the P1/P3 Scallop and the height of the P2 Scallop are the most critical elements, representing the radius of the whole Mitral Annulus.
Final 3D model
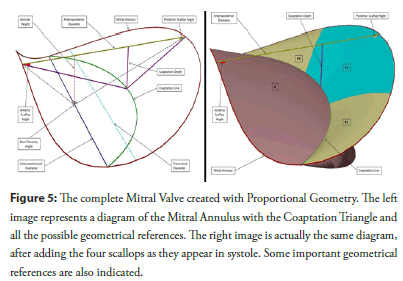
The Mitral Valve is well known to have a complex 3D geometry, with a saddle shaped annulus and a specific interaction among its scallops. Integrating the fractal scalar patterns of both the Coaptation Triangle and the scallop geometry we described previously, a complete 3D model can be obtained which describes the whole structure of the Mitral Valve in term of Fractals and Golden Proportion. In summary, the whole valve can be imagined as a set of components interacting like the pieces of a puzzle; components whose dimensional aspect and relationships are strictly related one another by Golden Ratio and fractal pattern, in an arrangement we could define “Proportional Geometry”. A complete description of this peculiar 3D geometrical structure is presented in Figure 5.
Figure 5: The complete Mitral Valve created with Proportional Geometry. The left image represents a diagram of the Mitral Annulus with the Coaptation Triangle and all the possible geometrical references. The right image is actually the same diagram, after adding the four scallops as they appear in systole. Some important geometrical references are also indicated.
Such a 3D model could have important implications for valve assessment: Once identified a healthy component or a normal dimension to start from, we could be able to predict the whole normal valve geometry using a single number (the Golden Number) and performing very easy calculations only. Alternatively, should a starting measurement not be identifiable, we could use for this purpose the expected normal valve diameters given by the many existing normograms, which correlate valve dimensions with patient’s BSA [33-35].
Table 1 is an example of how calculations can be made, starting from the Anteroposterior Diameter, to obtain the most significant geometrical references of the whole Mitral Valve.
Imaging Measurements and References
As mentioned before, we have thereafter reviewed the geometrical references routinely employed for the whole diagnosis and conservative treatment process, comparing them with the corresponding ones obtained from the 3D geometrical model based on the Golden Ratio and the set of calculations used to describe it.
To transform these calculations into concrete numbers and to use them for explanatory examples, we can consider an average individual, 175 cm tall. According to Lorentz, Robinson and Devine formulas, this leads to an ideal weight of 70 Kg and a BSA of 1.85 m2. According to the previously cited normograms [33-35], his average mitral Anteroposterior Diameter results around 29 mm.
Coaptation depth and height
Coaptation Depth is retrieved from the Coaptation Triangle and represents its height: The distance of the Coaptation Point below the anteroposterior diameter (Figure 2 and Figure 5). Originally born for surgical mitral repair, it has progressively been extended to interventional procedures, mainly percutaneous edge-to-edge repair. An increase in its value is an important sign of leaflet tethering, while a reduction indicates either chordal elongation or annular flattening. In literature, most authors report normal values between 6 and 8 mm [25,36-48]. Only Zhang found slightly lower values, around 4.2 mm [24].
Considering Proportional Geometry 3D model, the Coaptation Depth is given by APD/Φ3=APD/4.236 (Table 1) and the average individual previously cited has a Coaptation Depth of 29/4.236=6.85 mm, perfectly within the normality range.
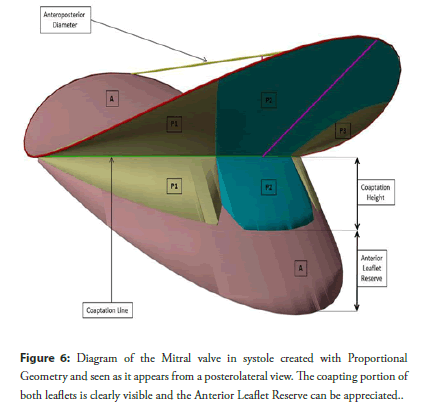
The Coaptation Height represents the length of the coapting portion of both leaflets below the Coaptation Point and gives an idea of how much valve tissue is involved in coaptation (Figure 2 and Figure 6). A reduction in this value indicates either annular dilatation or leaflet tethering and implies an unstable coapting surface. As for the Coaptation Depth, most of authors agree in considering normal and reliable values around 5-7 mm [48,49]. As we will see later, when dealing with the “Anterior Leaflet Reserve”, the Coaptation Height is, in fact, represented only by the lenght of the P2 Scallop below the Coaptation Point.
In Proportional Geometry 3D model, this value is again given by APD/Φ3=APD/4.236, the same identical calculation used for the Coaptation Depth (Table 1).
| Dimensions | Formula (with symbols) | Formula (with values) |
|---|---|---|
| Anterior Scallop Width | APD × Φ | APD × 1.618 |
| Anterior Scallop Height | APD | APD |
| P2 Scallop Width | APD | APD |
| P2 Scallop Height | APD/Φ | APD/1.618 |
| P1/P3 Scallop Width | APD/Φ | APD/1.618 |
| P1/P3 Scallop Height | APD/Φ2 | APD/2.618 |
| Annular Perimeter Radius | APD/Φ | APD/1.618 |
| Transverse Diameter | APD × 2/Φ | APD × 1.236 |
| Intercommissural Diameter | APD × 2 × 0.966/Φ | APD × 1.194 |
| Anterior Annular Length | APD × Φ | APD × 1.618 |
| Posterior Annular Length | APD × (2+Φ)/Φ | APD × 2,236 |
| Anterior Scallop Cord | APD/Φ | APD/1.618 |
| Posterior Scallop Cord | APD/Φ2 | APD/2.618 |
| Coaptation Depth | APD/Φ3 | APD/4.236 |
| Anterior Scallop Coaptation Height | APD/Φ2 | APD/2.618 |
| Posterior Scallop Coaptation Height | APD/Φ3 | APD/4.236 |
| Anterior Leaflet Reserve | APD/Φ4 | APD/6.854 |
Abbreviations: APD=Anteroposterior Diameter; Φ= 1.618.... (Golden Number)
Table 1: Possible calculations using the anteroposterior diameter as starting reference.
Concerning percutaneous edge-to-edge, literature is generally oriented to consider this procedure safely feasible when the Coaptation Depth is <11 mm and the Coaptation Height >2 mm [50], even if some recent studies have hypothesized good result extending indications beyond these cutoffs [51-53]. These limits are deeply related one another and easily explainable considering the average patient described previously, with both the Coaptation Depth and the Coaptation Height of 7 mm. A simple leaflet tethering (without annular dilatation) leading to a Coaptation Depth of 11 mm means a 4 mm displacement of the Coaptation Point towards the ventricular apex and an identical reduction of the Coaptation Height, which becomes 3 mm long: Just a little bit >2 mm, the shortest allowed dimension for a safe clip positioning.
Anterior leaflet reserve
In 2010, Gogoladze et al. [41] revealed an interesting characteristic of the Coaptation Height. The portion of Anterior Scallop below the Coaptation Point is longer than the corresponding one of P2 Scallop. In other words, there is a short terminal portion of Anterior Scallop which does not participate in coaptation. Therefore, the true Coaptation Height depends only on P2 Scallop (Figure 2 and Figure 6). Imaging techniques easily show the thicker tissue portion where the two Scallops pair together, but poorly evidence the lonely terminal part of Anterior Scallop, hardly distinguishable from the chordal apparatus. The authors define this excess of Anterior Scallop “Anterior Leaflet Reserve” and state that this element allows the valve to partially tolerate annular dilatation: In the early phases of this process, the Anterior Scallop slides anteriorly and uses its reserve to keep a normal Coaptation Surface.
The Proportional Geometry 3D model produces exactly the same result: The Anterior Scallop Coaptation Height is APD/ Φ2=APD/2.618, while the Posterior Scallop Coaptation Height is APD/Φ3= APD/4.236. The Anterior Leaflet Reserve is then the difference between the two measurements, thus APD/2.618- APD/4.236=APD × 0.145. Interestingly, this corresponds to APD/Φ4=APD/6.854 (Table 1). The average individual we cited previously has an Anterior Leaflet Reserve of 29 × 0.145=4.2 mm.
This information could potentially have an impact on percutaneous Neochord implantation, particularly when treating the Anterior Leaflet [54,55]. Repair could potentially result more reliable and durable if chordal adjustment considers not only the disappearance of regurgitation at real time echocardiography, but also the recreation of an Anterior Leaflet Reserve. Colli et al. state that after chordal adjustment under echo guidance a slight overtension should be applied to prevent recurrent regurgitation when the ventricle undergoes reverse remodeling [56].
Tenting area
This is another important measurement and corresponds to the area of the Coaptation Triangle (Figure 2 and Figure 5). An increase in this area is important indicator of leaflet tethering or annular dilatation [23,26,27]. Most authors report normal values to be around 100 mm2 [40,48,57,58], even if some authors found values of about 66 mm2 [24, 25].
Since in Proportional Geometry 3D model the Coaptation Depth corresponds to APD/Φ3=APD/4.236, the Tenting Area is given by APD × APD/Φ3/2=APD2/2Φ3=APD2/8.472 (Table 1).
In our average individual the Tenting Area results 292/8.472=99.268 mm2, which is again in accordance with literature [25, 40, 57,58].
AL/PL ratio
This ratio is a recent index and deserves another bit of explanation. The base of the Coaptation Triangle is divided by its height into two different segments, named “leaflet cords”, since they represent the geometrical projections of the Anterior Scallop and the P2 Scallop on the Anteroposterior Diameter (Figure 2).
The ratio between these two values is called “Anterior Leaflet to Posterior Leaflet Ratio” and estimates the horizontal position of the Coaptation Point. An increased ratio indicates a posterior displacement in the Coaptation Point, most commonly given by annular dilatation. On the contrary, a reduction in this ratio suggests an anterior shift of the Coaptation Point, which is a risk factor for Systolic Anterior Movement (SAM) development [27]. Recent investigations after valve repair concluded that an AL/PL Ratio below 1.5 significantly increases the risk for SAM [27,59,60]. Particularly, Maslow et al found that repaired valves had a tendency to SAM depending on the AL/PL Ratio, being maximum with values about 0.69 and completely absent when around 1.78 [61].
Proportional Geometry 3D model gives a value which is, by definition, 1.618. To detail this result we have to consider that the Anterior Leaflet Cord is APD/Φ=APD/1.618 and the Posterior Leaflet Cord is APD/Φ2= APD/2.618 (Table 1). Their ratio is then=(APD/Φ)/(APD/Φ2)=(APD/1.618)/ (APD/2.618)=(APD/1.618) × (2.618/APD) = 1.618, regardless of valve dimensions. Anyway, even this result agrees with literature findings.
Leaflet angles
The angles formed by the Anterior Scallop and the P2 Scallop with the Anteroposterior Diameter in systole are another significant index retrievable from the Coaptation Triangle (Figure 2 and Figure 5).
An increase in their values indicates leaflet tethering, while a reduction suggests a chordal elongation or an annular flattening. Some recent papers reported normal values to be around 27 degrees for the anterior leaflet and 30 degrees for the posterior one [25,40,48,62]. Again, the work by Zhang et al. found lower values, 12 degrees and 17 degrees, respectively [24]. The same papers also evidenced that a posterior leaflet angle >45 degrees is an index of severe leaflet tethering and a risk factor for failure after surgery.
In Proportional Geometry 3D model, angles are actually constant, regardless of valve dimensions. These two values result 21 degrees for the Anterior Scallop and 31.8 degrees for the Posterior Scallop, very close to literature data.
Annular saddling (AHCWR and non-planarity angle)
As already demonstrated, Mitral Annulus is not a flat structure, but has a characteristic 3D saddled shape. Because of this geometry the Intercommissural Diameter and the Anteroposterior Diameter lie on two different planes. The vertical gap between these two planes is called Annular Height and, interestingly, corresponds to the Coaptaton Depth (Figure 5).
One of the most important indexes of annular saddling is the ratio between the Annular Height and the Intercommissural Diameter, often expressed as a percentage. This ratio is called “Annular Height to Commissural Width Ratio” or “AHCWR”. However, to better understand this ratio, a base concept must be taken into account. The Intercommissural Diameter does not correspond to the Transverse Diameter: While the latter represents the maximum annular dimension (twice the radius), the former is a bit shorter, since located in a more anterior position (Figure 5).
Several studies state that normal valves show an AHCWR around 20%, with ranges between 15% and 30% (27, 36, 63, 64). A value <15% indicates a significant flattening of the annular saddle, often occurs with annular dilatation and implies a higher mechanical stress on valve tissue and chordae [63].
In Proportional Geometry 3D model, the Intercommissural Diameter corresponds to the Transverse Diameter multiplied by 0.966. Since the annular radius is APD/Φ, the Intecommissural Diameter results APD × 2 × 0.966/Φ (Table 1). In the same model, the Annular Height is equal to the Coaptation Depth, which is APD/Φ3 (Table 1). Considering these aspects, the AHCWR is then given by (APD/Φ3)/(APD × 2 × 0.966/Φ)=(APD/4.236)/ (APD × 1.194)=1/(4.236 × 1.194)=1/5.058=0.198=19.8%. Once more in accordance with values found in literature.
Another important index of annular saddling is the “Non- Planarity Angle”, which carries the same kind of information as the AHCWR. It is actually the angle formed by two ideal lines starting at the extremities of the Anteroposterior Diameter and meeting in the middle of the Intercommissural Diameter (Figure 5). Literature data report a value of about 120 degrees in normal valves [64,65] and state that an increase in this angle is an important sign of loss of the annular saddle, due to annular dilatation and flattening. Some authors, however, consider pathological values of such an angle when >158 degrees [48,66,67].
As we said previously, in Proportional Geometry 3D model all angles are constant, regardless of valve dimension. Anyway, in this 3D model, the Non-Planarity angle results to be 121.7 degrees wide, again in accordance with literature.
Leaflet-to-Annulus Index (LAI)
Leaflet-to-Annulus Index or “LAI” is a quite recent reference and is defined as the sum of the heights of the Anterior Scallop and the P2 Scallop divided by the Anteroposterior Diameter in systole. Actually, it estimates how much valve tissue is available to create the coapting leaflet surface in systole. It has nowadays become extremely popular for interventional procedures, such as percutaneous Edge-to-Edge or Transapical Off-Pump Neochord implantation. A consistent number of studies states that the best procedural results occur when its value is >1.25 and, in accordance with these results, many researchers suggest an additional annuloplasty when this value is below this limit [68, 69]. Colli et al. agree with these results, even if report a good feasibility of percutaneous Neochord implantation with LAI lower than this cutoff [56,70].
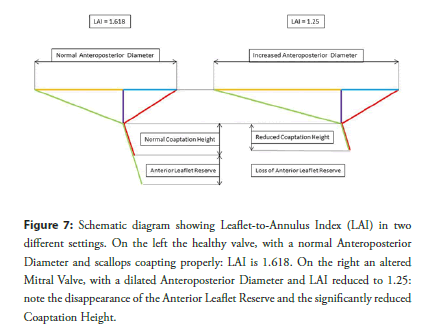
Once more, applying the calculations of Proportional Geometry 3D model, LAI results to be (APD+APD/Φ)/APD = (APD+APD/1.618)/ APD=APD/APD+1/1.618=1+0.618=1.618 (Table 1): Well above the limit of 1.25. Additionally, using the same calculations, we can also hypothesize an explanation of this cutoff. In our average individual, the Anteroposterior Diameter is 29 mm long, the height of the Anterior Scallop (equal to APD) again 29 mm and the height of the P2 Scallop (APD/1.618) 29/1.618=18 mm. In systole, the Anterior Scallop Coaptation Height is APD/2.618=11 mm and the P2 Scallop Coaptation Height APD/4.236=7 mm. In such a setting, the Coaptation Height is 7 mm, the Anterior Leaflet Reserve 4 mm and LAI results exactly 1.618. Considering the valve scallops unchanged, a LAI reduction to 1.25 means an increase in the Anteroposterior Diameter to about 37 mm, 8 more than the expected. A valve with such a modification, actually, has completely run out of its Anterior Leaflet Reserve (4 mm) and has also reduced its Coaptation Height to only 5 mm, 2 mm less per each scallop, critically impairing its own coaptation stability (Figure 7).
Figure 7: Schematic diagram showing Leaflet-to-Annulus Index (LAI) in two different settings. On the left the healthy valve, with a normal Anteroposterior Diameter and scallops coapting properly: LAI is 1.618. On the right an altered Mitral Valve, with a dilated Anteroposterior Diameter and LAI reduced to 1.25: note the disappearance of the Anterior Leaflet Reserve and the significantly reduced Coaptation Height.
Annuloplasty
Reduction and stabilization of Mitral Annulus is mandatory when repair is performed surgically. However, even during percutaneous interventions, annuloplasty might be necessary either to accomplish the procedure or to improve its result. Nowadays, several percutaneous devices are available, which act either directly or indirectly on the posterior Mitral Annulus, and literature on their employment is constantly growing [71-77]. However, no specific geometrical reference actually exists to estimate the amount of annular reduction and real-time echo guidance is the only reference used to decide and evaluate annuloplasty entity.
Once more, Proportional Geometry 3D model could give some help in this direction. In this model, the Posterior Annulus is APD × (2+Φ)/Φ=APD × (2+1.618)/1.618 APD × 3.618/1.618=APD ×2.236 (Table 1). This value represents the posterior annular length from Commissure to Commissure and, in our average patient, it results 29 × 2.236=64.844 mm, being again in accordance with literature [38]. The ability to predict the estimated normal length of the posterior Mitral Annulus could then result an important reference to guide annuloplasty.
Conclusion
Proportional Geometry 3D Mitral model appears to represent the whole structure of the healthy Mitral Valve in a reliable way. Starting from a single reference measurement and employing very easy calculations, it seems able to predict the expected normal dimensions and shape of every valve component, leading to results similar or almost identical to those observed in literature.
Another important aspect of this model is that it is entirely based on proportions rather that absolute values, tailoring the valve on patient’s size. Commonly, when dealing with valve measurements, values are given in term of normality ranges, which include the vast majority of adult individuals. However, part of the world population, such as children or people with extremely small or big body sizes, could produce both false positives and false negatives. In these specific subgroups, calculations based on Proportional Geometry rules could provide more significant values, leading to identify with more reliability both healthy and pathological aspects.
Even if further studies are needed to give it a stronger statistical significance, this model could result helpful for performing both surgical and interventional procedures, allowing operators to be more accurate in their actions and leading them to tend to a precise final target.
Additionally, since in such a 3D model every geometrical aspect can be studied and calculated, it could also be helpful for investigating measurements and geometrical references, which could be discovered in the future.
Funding
None.
Conflict of Interest
The author declares that there is no conflict of interest regarding the publication of this article.
References
- Deorsola L, Bellone A. Coaptation triangle and Golden Proportion in mitral valve anatomy. Does Nature play with geometry? Echocardiography. 35(1): 30-38 (2018).
- Deorsola L, Bellone A. The Golden Proportion in the scallop geometry of normal mitral valves. When Nature plays with jigsaw puzzles. Echocardiography. 36(6): 1-7 (2019).
- Euclid. Elements. Book 2, Propositions 11; Book 4, Propositions 10-11; Book 6, Propositions 3-30; Book 13, Propositions 1-6, 8-11, 16-18.
- Pacioli L. De Divina Proportione. Venice, Italy: Paganinus de Paganinus. 1509.
- Livio M. The Golden Ratio: The story of phi, the world's most astonishing number. New York, NY: Broadway Books; (2002).
- Coldea R, Tennant DA, Wheeler EM, et al. Quantum criticality in an ising chain: Experimental evidence for emergent E8 symmetry. Science. 5962: 177-180 (2010).
- Yamagishi MEB, Shimabukuro AI. Nucleotide frequencies in human genome and Fibonacci numbers. Bull Math Biol. 70(3): 643-53 (2008).
- Losa M, Fusco A, Marchetti F, et al. The Golden Ratio of gait harmony: Repetitive proportions of repetitive gait phases. Biomed Res Int. 1: 1-7 (2013).
- Okabe T. Physical phenomenology of phyllotaxis. J Theor Biol. 280: 63-75 (2011).
- Ferring V, Pancherz H. Divine Proportions in the growing face. Am J Orthod Dentofacial Orthop. 134(4): 472-479 (2008).
- Ricketts RM. Divine Proportion in facial esthetics. Clin Plast Surg. 9(4): 401-422 (1982).
- Russell PA. The aesthetics of rectangle proportion: Effects of judgment scale and context. Am J Psychol. 131(1): 27-42 (2000).
- Henein MY, Zhao Y, Nicoll R, et al. The human heart: Application of the Golden Ratio and angle. Int J Cardiol. 150(3): 239-242 (2011).
- Sharif RAL. Golden Ratio in architecture and the human heart. IJSER. 5: 1529-1541 (2014).
- Persuad-Sharma D, O'Leary JP. Fibonacci Series, Golden Proportions, and the human biology. Austin J Surg. 2: 1-6 (2015).
- Chan JY, Chang GH. The Golden Ratio optimizes cardiomelic form and function. Irn J Med Hypotheses Ideas. 3: 2-6 (2009).
- Guinnes GI. Companion encyclopedia of the history and philosophy of the mathematical sciences. Baltimore, MD: The Johns Hopkins University Press; 2003.
- Mandelbrot B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science. 156(3): 636-638 (1967).
- Meyer HV, Dawes TJW, Serrani M, et al. Genetic and functional insights into the fractal structure of the heart. Nature. 584(7822): 589-594 (2020).
- Captur G, Karperien AL, Hughes AD, et al. The fractal heart-Embracing mathematics in the cardiology clinic. Nat Rev Cardiol. 14(1): 56-64 (2017).
- Brown JH, Gupta VK, Li BL, et al. The fractal nature of Nature: Power laws, ecological complexity and biodiversity. Philos Trans R Soc Lond B Biol Sci. 357(1421): 619-26 (2002).
- Ramírez JL, Rubiano GN, De Castro R. A generalization of the Fibonacci word fractal and the Fibonacci snowflake. Theor Comput Sci. 528: 40-56 (2014).
- Karaca O, Avci A, Guler GB, et al. Tenting area reflects disease severity and prognosis in patients with non-ischaemic dilated cardiomyopathy and functional mitral regurgitation. Eur J Heart Fail. 13: 284-291 (2011).
- Zhang L, Qiu J, Yu L, et al. Quantitative assessment of mitral apparatus geometry using dual-source computed tomography in mitral regurgitation. Int Heart J. 56(4): 408-414 (2015).
- Dudzinski DM, Hung J. Echocardiographic assessment of ischemic mitral regurgitation. Cardiovasc Ultrasound. 12: 46-61 (2014).
- Agricola E, Oppizzi M, Pisani M, et al. Ischemic mitral regurgitation: Mechanisms and echocardiographic classification. Eur J Echocardiography. 9(2): 207-221 (2008).
- Mahmood F, Matyal R. A quantitative approach to the intraoperative echocardiographic assessment of the mitral valve for repair. Anesth Analg. 121: 34-58 (2015).
- Rusted IE, Scheifley CH, Edwards JE. Studies of the mitral valve. I. Anatomic features of the normal mitral valve and associated structures. Circulation. 6(6): 825-831 (1952).
- Morris EWT. Some features of the mitral valve. Thorax. 15(1): 70-73 (1960).
- Du Plessis LA, Marchand P. The anatomy of the mitral valve and its associated structures. Thorax. 19(3): 221-227 (1964).
- Ranganathan N, Lam JHC, Wigle ED, et al. Morphology of the human mitral valve: II. The valve leaflets. Circulation. 41(3): 459-467 (1970).
- Walmsley R. Anatomy of human mitral valve in adult cadaver and comparative anatomy of the valve. Br Heart J. 40(4): 351-366 (1978).
- Rowlatt JF, Rimoldi JHA, Lev M. The quantitative anatomy of the normal child’s heart. Pediatr Clin North Am. 10(2): 499-506 (1963).
- Westaby S, Karp RB, Blackstone EH, et al. Adult human valve dimensions and their surgical significance. Am J Cardiol. 53(4): 552-558 (1984).
- Sonne C, Sugeng L, Watanabe N, et al. Age and body surface area dependency of mitral valve and papillary apparatus parameters: Assessment by real-time three-dimensional echocardiography. Eur J Echocardiography. 10(2): 287-294 (2009).
- Lee APW, Hsiung MC, Salgo IS, et al. Quantitative analysis of mitral valve morphology in mitral valve prolapse with real-time 3-dimensional echocardiography. Importance of annular saddle shape in the pathogenesis of mitral regurgitation. Circulation. 127(7): 832-841 (2013).
- Ryan LP, Jackson BM, Enomoto Y, et al. Description of regional mitral annular nonplanarity in healthy human subjects: A novel methodology. J Thorac Cardiovasc Surg. 134(3): 644-648 (2007).
- Pouch AM, Vergnat M, McGarvey JR, et al. Statistical assessment of normal mitral annular geometry using automated three-dimensional echocardiographic analysis. Ann Thorac Surg. 97(1): 71-77 (2014).
- Grewal J, Suri R, Mankad S, et al. Mitral annular dynamics in myxomatous valve disease: New insights with real-time 3-dimensional echocardiography. Circulation. 121(12): 1423-1431 (2010).
- Magne J, Pibarot P, Dagenais F, et al. Preoperative posterior leaflet angle accurately predicts outcome after restrictive mitral valve annuloplasty for ischemic mitral regurgitation. Circulation. 115(6): 782-791 (2007).
- Gogoladze G, Dellis SL, Donnino R, et al. Analysis of the mitral coaptation zone in normal and functional regurgitant valves. Ann Thorac Surg. 89(4): 1158-1161 (2010).
- Ryan LP, Jackson BM, Eperjesi TJ, et al. Quantitative description of mitral valve geometry using real-time three-dimensional echocardiography. Innovations. 2(5): 237-244 (2007).
- Calafiore AM, Gallina S, Di Mauro M, et al. Mitral valve procedure in dilated cardiomyopathy: Repair or replacement? Ann Thorac Surg. 71(4): 1146-1152 (2001).
- Donal E, Levy F, Tribouilloy C. Chronic ischemic mitral regurgitation. J Heart Valve Dis. 15: 149-157 (2006).
- Hayashi T, Inuzuka R, Shindo T, et al. Clinical implications of mitral valve geometric alterations in children with dilated cardiomyopathy. Cardiol Young. 26(7): 1365-1372 (2016).
- Lim E, Ali ZA, Barlow CW, et al. Determinants and assessment of regurgitation after mitral valve repair. J Thorac Cardiovasc Surg. 124: 911-917 (2002).
- Adams DH, Rosenhek R, Falk V. Degenerative mitral valve regurgitation: Best practice revolution. Eur Heart J. 31(16): 1958-1966 (2010).
- Oliveira D, Srinivasan J, Espino D, et al. Geometric description for the anatomy of the mitral valve: A review. J Anat. 237(2): 209-224 (2020).
- Wei D, Han J, Zhang H, et al. The correlation between the coaptation height of mitral valve and mitral regurgitation after mitral valve repair. J Cardiothorac Surg. 12: 120-124 (2017).
- Lesevic H, Karl M, Braun D, et al. Long-term outcomes after MitraClip implantation according to the presence or absence of EVEREST inclusion criteria. Am J Cardiol. 119(8): 1255-1261 (2017).
- Gössl M, Sorajja P. MitraClip patient selection: Inclusion and exclusion criteria for optimal outcomes. Ann Cardiothorac Surg. 7(6): 771-775 (2018).
- Attizzani GF, Ohno Y, Capodanno D, et al. Extended use of percutaneous edge-to-edge mitral valve repair beyond EVEREST (Endovascular Valve Edge-to-Edge Repair) criteria: 30-day and 12-month clinical and echocardiographic outcomes from the GRASP (Getting Reduction of Mitral Insufficiency by Percutaneous Clip Implantation) registry. JACC: Cardiovasc Interv. 8(1): 74-82 (2015).
- Shah M, Jorde UP. Percutaneous mitral valve interventions (repair): Current indications and future perspectives. Front Cardiovasc Med. 6: 1-18 (2019).
- Colli A, Manzan E, Zucchetta F, et al. Feasibility of anterior mitral leaflet flail repair with transapical beating-heart NeoChord implantation. JACC: Cardiovasc Interv. 7(11): 1320-1321 (2014).
- Ahmed A, Abdel-Aziz TA, Al Asaad MMR, et al. Transapical off-pump mitral valve repair with NeoChord implantation: A systematic review. J Card Surg. 36(4):1492-1498 (2021).
- Colli A, Adams D, Fiocco A, et al. Transapical NeoChord mitral valve repair. Ann Cardiothorac Surg. 7(6): 812-820 (2018).
- Kongsaerepong V, Shiota M, Gillinov AM, et al. Echocardiographic predictors of successful versus unsuccessful mitral valve repair in ischemic mitral regurgitation. Am J Cardiol. 98(4): 504-508 (2006).
- Cummisford KM, Manning W, Karthik S, et al. 3D TEE and systolic anterior motion in hypertrophic cardiomyopathy. JACC Cardiovasc Imaging. 3(10): 1083-1084 (2010).
- Ragab A, Mahfouz MD. Utility of the posterior to anterior mitral valve leaflets length ratio in prediction of outcome of percutaneous balloon mitral valvuloplasty. Echocardiography. 28(10): 1068-1073 (2011).
- Yoshimura M, Kunisawa T, Iida T, et al. Preoperative morphological analysis by transesophageal echocardiography and predictive value of plasma landiolol concentration during systolic anterior motion mitral valve repair: a report of three cases. J Anesth. 28(3): 452-455 (2014).
- Maslow AD, Regan MM, Haering JM, et al. Echocardiographic predictors of left ventricular outflow tract obstruction and systolic anterior motion of the mitral valve after mitral valve reconstruction for myxomatous valve disease. J Am Coll Cardiol. 34(7): 2096-2104 (1999).
- Lee AP, Acker M, Kubo SH, et al. Mechanisms of recurrent functional mitral regurgitation after mitral valve repair in nonischemic dilated cardiomyopathy. Importance of distal anterior leaflet tethering. Circulation. 119(19): 2606-2614 (2009).
- Salgo IS, Gorman III JH, Gorman RC, et al. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 106(6): 711-717 (2002).
- Mahmood F, Subramaniam B, Gorman III JH, et al. Three-dimensional echocardiographic assessment of changes in mitral valve geometry after valve repair. Ann Thorac Surg. 88(6): 1838-1844 (2009).
- Saracino G, Daimon M, Greenberg NL, et al. A novel system for the assessment of mitral annular geometry and analysis of 3D motion of the mitral annulus from 3D echocardiography. Comput Cardiol 31: 69-72 (2004).
- Sun X, Jiang Y, Huang G, et al. Three-dimensional mitral valve structure in predicting moderate ischemic mitral regurgitation improvement after coronary artery bypass grafting. J Thorac Cardiovasc Surg. 157(5): 1795-1803 (2019).
- Bouma W, Gorman RC. Commentary: Three-dimensional P3 tethering angle at the heart of future surgical decision making in ischemic mitral regurgitation. J Thorac Cardiovasc Surg. 157(5): 1806-1807 (2019).
- Tabata N, Weber M, Sugiura A, et al. Impact of the leaflet-to-annulus index on residual mitral regurgitation in patients undergoing edge-to-edge mitral repair. JACC: Cardiovasc Interv. 12(24): 2462-2472 (2019).
- Colli A, Besola L, Montagner M, et al. Prognostic impact of leaflet-to-annulus index in patients treated with transapical off-pump echo-guided mitral valve repair with NeoChord implantation. Int J Cardiol. 257: 235-237 (2018).
- Colli A, Bizzotto E, Manzan E, et al. Patient-specific ventricular access site selection for the NeoChord mitral valve repair procedure. Ann Thorac Surg. 104(2): 199-202 (2017).
- Gasior T, Gavazzoni M, Taramasso M, et al. Direct percutaneous mitral annuloplasty in patients with functional mitral regurgitation: When and how. Front Cardiovasc Med. 6: 2-13 (2019).
- Nickenig G, Hammerstingl C, Schueler R, et al. Transcatheter mitral annuloplasty in chronic functional mitral regurgitation 6-month results with the cardioband percutaneous mitral repair system. IACC: Cardiovasc Interv. 9(19): 2039-2047 (2016).
- Krishnaswamy A, Kapadia SR. Indirect mitral annuloplasty using the carillon device. Front Cardiovasc Med. 7: 1-6 (2020).
- Messika-Zeitoun D, Nickenig G, Latib A, et al. Transcatheter mitral valve repair for functional mitral regurgitation using the Cardioband system: 1 year outcomes. Eur Heart J. 40(5): 466-472 (2019).
- Nickenig G, Hammerstingl C. The Mitralign transcatheter direct mitral valve annuloplasty system. Euro Interv. 11: 62-63 (2015).
- Schueler R, Nickenig G. The Mitralign: Strategies for optimal patient selection and optimised results. Euro Interv. 12: 67-69 (2016).
- Rogers JH, Boyd WD, Smith TW. Early experience with Millipede IRIS transcatheter mitral annuloplasty. Ann Cardiothorac Surg. 7(6): 780-786 (2018).