Prediction of post-operative clinical parameters in  posterior scoliosis surgery using an adaptive neuro- fuzzy interface system

Abedi Rasoul

doi:10.37532/2041-6792.2023.13(3).402-408

Research Article - Clinical Investigation (2023) Volume 13, Issue 3

Prediction of post-operative clinical parameters in posterior scoliosis surgery using an adaptive neuro- fuzzy interface system

Abedi Rasoul^*

Department of Biomedical Engineering, Amirkabir University of Technology, Tehran, Iran

Corresponding Author:: Abedi Rasoul
Department of Biomedical Engineering, Amirkabir University of Technology, Tehran, Iran
E-mail: abedi.rasoul1990@gmail.com

Received: 07-March-2023, Manuscript No. fmci-23-91053; Editor assigned: 09-March-2023, Pre-QC No. fmci-23-91053 (PQ); Reviewed: 11-March-2023, QC No. fmci-23-91053 (Q); Revised: 18-March -2023, Manuscript No. fmci-23-91053 (R); Published: 30-March-2023; DOI: 10.37532/2041-6792.2023.13(3).402-408

Abstract

Background and Objective: Postoperative clinical indices should be estimated accurately in scoliosis correction surgeries, which have been analyzed in various studies such as experimental (in vitro or in vivo) trials through different modeling methods (finite element or multibody analysis). These costly and timeconsuming methods can only be conducted on a large number of scoliotic patients. An adaptive neurofuzzy interface system (ANFIS) is used in this study to estimate the postoperative cobb and thoracic kyphosis angles in adolescent idiopathic scoliosis patients undergoing posterior scoliosis correction surgeries.
Methods: Four groups of 55 patients with distinct preoperative clinical indices (thoracic cobb and pelvic incidence) were considered the ANFIS inputs, whereas postoperative thoracic cobb and kyphosis angles were used as the outputs. For robustness evaluation, the predicted values of postoperative angles were compared with measurements by calculating the root mean square errors and clinical correction deviation indices (the relative deviation of postoperative predicted angles from the real angles).
Results: The least root mean square errors (3.0º and 6.3° for the main thoracic cobb and thoracic kyphosis estimations, respectively) were recorded in the group with the main thoracic cobb, pelvic incidence, thoracic kyphosis, and T1 spinopelvic inclination used as inputs. The clinical correction deviation indices were calculated 0.0086 and 0.0641 for cobb angles in two cases and 0.0534 and 0.2879 for thoracic
kyphosis in two other cases.
Conclusion: Greater differences between preoperative and postoperative cobb angles compared with those of thoracic kyphosis decreased the root-mean-square errors and clinical deviation indices but improved accuracy.

Keywords

Cobb angle • Pelvic incidence • Scoliosis correction • Spine • Thoracic kyphosis

Introduction

Scoliosis is a type of 3D spinal deformity that emerges mostly in the frontal plane at different regions, e.g., thoracic and/or lumbar [1]. The adolescent idiopathic scoliosis has been considered a growing research issue in recent years [2, 3]. The prevalence of scoliosis is 2% to 4% in adolescents. It is ten times more common in female cases than in male ones [4,5]. Generally, when the cobb angle formed in the frontal plane due to scoliosis exceeds 40° or 50°, the patient needs surgical correction [6-8]. Several experimental and modeling studies have been conducted to estimate postoperative indices in scoliosis correction surgeries [9-11].

The first group includes the experimental studies using in vitro or in vivo methods [12-14]. The in vitro studies have analyzed cadaveric specimens by utilizing surgical rods and screws to measure the forces exerted by surgical instruments and analyze spinal movements during deformity correction. They aim to assess the effects of surgical instruments and techniques on spinal fusion biomechanics on cadavers [9-12]. However, the in vivo studies employ force sensors on surgical devices and motion analysis to measure both kinetic parameters (e.g., force and moment) and kinematic parameters (e.g., angular displacement) throughout the real scoliosis correction surgery. In fact, these studies are aimed at analyzing the biomechanics of scoliosis fusion with their forces, moments, and rotation behaviors. Nevertheless, both in vitro and in vivo studies are limited and costly [13-15].

The second group includes the modeling studies that can be divided into two subgroups, i.e., Finite Element modeling (FEM) and Multibody Modeling (MBM) approaches. The FEM methods have usually used anatomical models of vertebrae, discs, and other soft tissues with different material properties [11, 16]. Some FEM studies have also employed the geometrical models of rods and screws to simulate the scoliosis correction surgery in different steps by exerting corrective forces and displacements [17, 18]. In the MBM methods, separate vertebral bodies as well as analytical and mathematical calculations are used in a functional model while using soft tissue effects as spring elements. These studies aim to develop detailed multibody models for scoliotic spine to analyze their mechanical behaviors and chain mechanism kinematics [19-21]. However, these modeling methods are time-consuming and limited due to the available case numbers for developing more general and practical methods.

The third group includes artificial intelligence studies using various machine learning algorithms such as neural networks, fuzzy logic, and clustering to analyze spinal biomechanics [22–24]. Neural network techniques have also been utilized for different purposes such as scoliosis detection or cobb angle estimation from upper body clinical indices in addition to determining spinal fusion patterns of different Lenke types [25-27]. These methods are characterized by the advantage of considering a large number of cases to estimate clinical parameters. However, the problem remains in minimizing estimation errors.

Hence, previous studies have not employed any straightforward approaches to predict postoperative angles in scoliosis surgery based on a large number of patients. This study aims to estimate the postoperative cobb and thoracic kyphosis angles in Adolescent Idiopathic Scoliosis (AIS) patients undergoing posterior scoliosis correction surgery. For this purpose, various arrangements of preoperative clinical indices were analyzed as the inputs of an Adaptive Neuro-Fuzzy Interface System (ANFIS). Afterwards, the postoperative clinical indices were employed to train and test an ANFIS that estimated these values in new scoliotic cases. The proposed approach is hypothesized to provide a more accurate yet easier instrument to estimate postoperative angles.

Methods

Collecting Patient Radiographs

The frontal and sagittal views of preoperative and postoperative radiographs of 55 AIS patients (49 females and 6 males) were collected by using an EOS radiography device at Shafa Yahyaian Hospital with the capability of bi-planar low-dose radiography in frontal and sagittal planes [28]. The patients were aged 15 ± 3 years old in different Lenke types. Undergoing posterior rod surgeries, 34 of them were classified as the Lenke type A

Measuring Clinical Indices

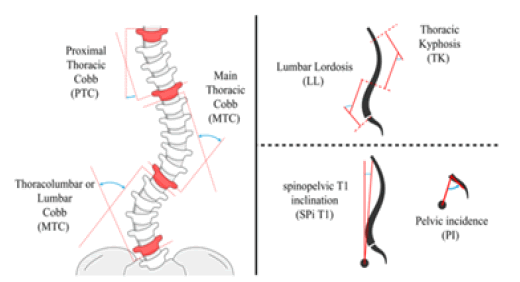
Preoperative Proximal Thoracic Cobb (PTC), Main Thoracic Cobb (MTC), Thoracolumbar Cobb (TLC), pelvic Incidence (PI), Thoracic Kyphosis (TK), Lumbar Lordosis (LL), and T1 Spinopelvic Inclination (T1 SPi) angles were measured in Surgimap (v2.3.2.1, A Nemaris Inc. Product, New York, USA), which is a commercial program for image processing (Figure 1). Postoperative MTC and TK angles were also measured as important guides to estimate postoperative spine curvatures. These clinical indices are usually utilized in the biomechanical analysis of scoliotic patients.

Figure 1: Clinical indices of scoliotic spine calculated in the frontal and sagittal planes

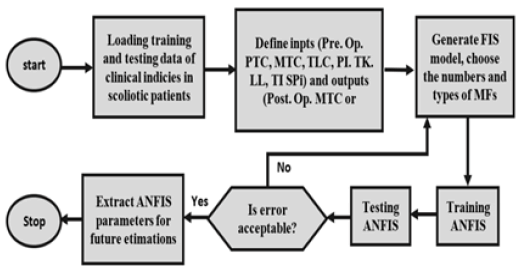
The ANFIS learning algorithm, which integrates neural networks with fuzzy methods, was employed and trained through the measured preoperative and postoperative clinical indices. Different arrangements of preoperative clinical indices were used as ANFIS inputs to compare their training outputs. Figure 2 demonstrates the flowchart of the ANFIS algorithm with input/preoperative and output/postoperative clinical indices. In the first layer of the ANFIS structure, preoperative clinical indices are used as the fuzzy logic inputs to divide them into several Membership Functions (MFs) in the next layer. The quantity of MFs was determined by trial and error to minimize the Root-Mean-Square Error (RMSE) of the postoperative MTC and TK estimations. The subtractive clustering method was then employed in the fuzzy interface system with the Sugeno model and Gaussian MFs.

Figure 2: ANFIS flowchart and structure for estimating postoperative main thoracic cobb (MTC) and thoracic kyphosis (TK) angles.

Four groups of preoperative indices were selected as ANFIS inputs (Table 1). The RMSE values of the estimated postoperative angles were compared in different states of selecting the preoperative inputs. This comparison was drawn to determine the least possible estimation error with the least possible number of inputs in frontal and sagittal planes. The procedure helped find the most appropriate input selections to estimate postoperative MTC and TK angles with the least possible errors.

Table 1. Classification of pre-operative clinical indices as ANFIS inputs in four groups

Group number	ANFIS inputs (pre-operative clinical indices)
Group 1	MTC, PI, TK
Group 2	MTC, PI, TK, TI SPi
Group 3	PTC, MTC, TLC, PI, TK, LL
Group 4	PTC, MTC, TLC, PI, TK, LL, TI SPi

The selected inputs were examined in two scoliosis types, i.e., all cases with all Lenke types (55 patients) and the cases with Lenke A type (34 patients). Moreover, the ANFIS analysis procedure was implemented by three different numbers of its fuzzy MFs to evaluate their effects (i.e., 35, 40, and 45 for all Lenke type cases and 15, 20, and 25 for Lenke A type cases) and to estimate the postoperative MTC and TK clinical indices.

Defining and Calculating Error and Deviation Index

In all ANFIS execution states, 85% of clinical input data were used for training, whereas the remaining 15% of data were used for clinical data testing. In fact, the testing procedure error denotes the difference between the real operated angles and the predicted clinical angles (i.e., postoperative MTC and TK). Furthermore, the relative deviation in the ANFIS prediction of postoperative MTC and TK angles from their real operated angles was defined as the clinical correction deviation index (CCDI). The RMSE and CCDI parameters were defined as below:

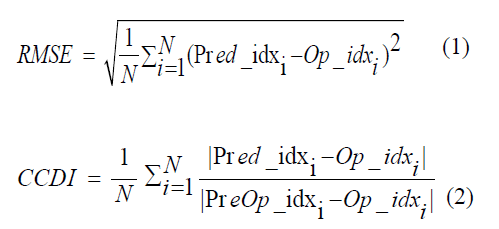
Where Op-idx, Pred-idx, and PreOp-idx represent the real postoperative outputs, ANFIS predictions for outputs, and the preoperative indices (inputs) of the tested data group, respectively (all values are expressed in degrees). In addition, four groups of test inputs (Table 1) were employed to verify the ANFIS and calculate RMSE and CCDI values in two modes: eight cases from 55 patients of all Lenke types and five cases from 34 patients of Lenke A type.

Results

RMSE and CCDI values

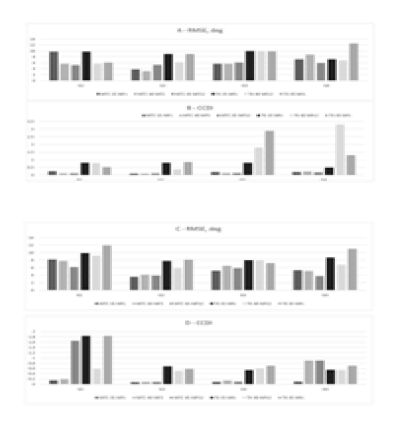
Generally, Group 2 (where MTC, PI, TK, and T1 SPi were used as ANFIS inputs) yielded the least RMSE and CCDI values. Figure 3 demonstrates the RMSE and CCDI values in four groups of 55 (all Lenke types) and 34 (Lenke A type) scoliotic cases. Accordingly, the RMSE and CCDI values of Group 2 were smaller than those of other groups in most cases. Furthermore, the CCDI values of postoperative MTC angles were significantly lower than those of postoperative TK angles. In certain circumstances such as that of Group 1, the RMSE values of postoperative MTC reduced as the number of MFs increase; however, those values increased in Group 3. Therefore, increasing the number of MFs did not necessarily change RMSE and CCDI values.

Figure 3: RMSE and CCDI parameters for 4 groups of ANFIS inputs in different numbers of membership functions (MFs), A: RMSE for all Lenke types (55 cases), B: CCDI for all Lenke types, C: RMSE for Lenke A type (34 cases), D: CCDI for Lenke A type

According to the comparison drawn between postoperative MTC and TK indices, the RMSE values of postoperative TK estimations were usually greater than those of MTC estimations. Furthermore, the CCDI values of TK were mostly and considerably higher than those of MTC. Moreover, the RMSE values for Lenke A type cases were greater than all Lenke types in Group 1, whereas they were smaller in Group 4. In addition, the CCDI values were greater for postoperative TK of Lenke A type than for all Lenke types in Group 1. However, they were significantly smaller in Groups 3 and 4

Although the number of MFs affected the RMSE or CCDI parameters, their effects did not follow a regular pattern but depended on the number of cases and ANFIS inputs. However, very few or many MFs increased the RMSE and CCDI values. Hence, an appropriate number of MFs should have been selected

to decrease those values. There was a clearer difference between postoperative MTC and TK estimations in CCDI than in RMSE, and the CCDI values of MTC were significantly smaller than those of TK (Figure. 3).

Post-operative MTC and TK prediction

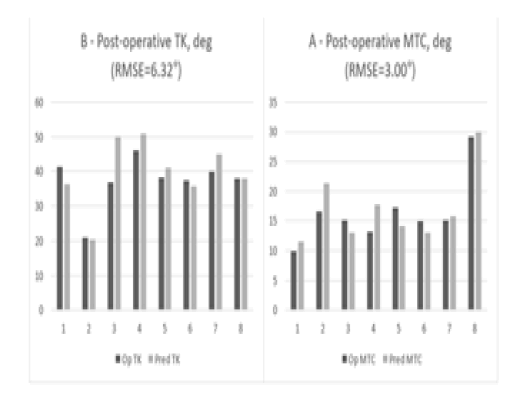
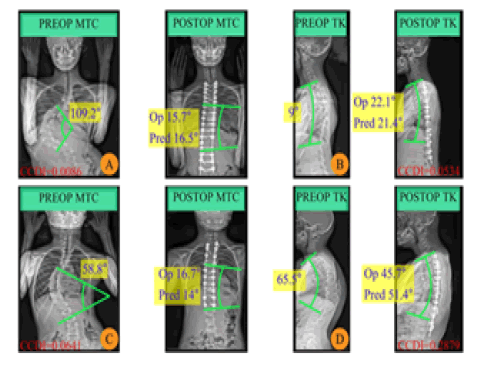
Since Group 2 had smaller RMSE and CCDI values, the results of this group were analyzed more accurately. For this purpose, the researchers analyzed the sample results of the operated and predicted values of the ANFIS outputs for postoperative MTC and TK angles in the test data of Group 2 (8 cases). Moreover, 40 MFs were used in the ANFIS for all Lenke types (Figure. 4). Four samples of operated and predicted results from Group 2 with 40 MFs were selected randomly (2 cases for MTC and 2 cases for TK estimation) in order to visualize the results. The preoperative (PREOP) and postoperative (POSTOP) MTC and TK angles were also illustrated in these cases (Figure. 5).

Figure 4: A sample comparison of Operated (Op) and Predicted (Pred) values for post-operative MTC and TK angles in test data of 8 scoliotic cases in group 2 with 40 membership functions.

Figure 5: Illustration of results in 4 scoliotic cases of group 2: pre-operative, operated (Op), and predicted (Pred) post-operative values for MTC (A and C) and TK (B and D) angles.

Cases A and D had the minimum and maximum CCDI values, respectively (Figure. 5). In Cases A and C, the differences between the operated and predicted results of postoperative MTC were reported 0.8º and 2.7°, respectively. However, these differences were reported 0.7º and 5.7º degrees in Cases B and D, respectively. Hence, the error values were higher in estimating postoperative TK than in estimating postoperative MTC. Moreover, preoperative and postoperative values had a greater difference in MTC than in TK

Discussion

The ANFIS algorithm helped accelerate the prediction of postoperative clinical indices and improve the work of surgeons. In fact, postoperative MTC and TK are among the most important clinical angles affecting the biomechanical parameters of spine and its stability. Hence, it is essential to estimate and predict these angles accurately

Limitations

The number of cases was limited. Evidently, more cases could lead to the better prediction of postoperative clinical indices. Various surgical methods of scoliosis correction such as translation, distraction, compression, and de-rotation techniques at different spine levels can affect the scoliotic curve during the correction procedure, something which was not addressed in this study. In other words, it is a too complicated process to be applied in the ANFIS algorithm.

Spinal stiffness (due to the intervertebral discs and ligaments) affects its curvature during scoliosis correction. However, the AIS cases had no data of real stiffness values, the effect of which was disregarded in this study. The ANFIS algorithm also includes only one output; thus, it is impossible to estimate multiple postoperative clinical angles simultaneously. As a result, there is a separate ANFIS for each of the postoperative MTC and TK angles having no interrelation to make concurrent estimations.

Analysis of results

Surgeons always try to reduce the cobb angle to its least possible value; thus, the reduction of MTC is evident after operation. However, this is not true about postoperative TK, for it increases after scoliosis correction surgery in some cases. This explains why RMSE values of postoperative TK were usually greater than those of MTC (especially in Group 2). Therefore, it is easier for the ANFIS algorithm to predict cobb angles leading to the lower values of RMSE. According to the CCDI definition, greater CCDI values in TK angles are generally due to smaller differences between preoperative and postoperative TK values than those between MTC values in nearly all groups. At the same time, a reduction in the CCDI indicates a reduction in the ANFIS estimation error (Figure. 3).

The RMSE and CCDI values of all Lenke types and those of Lenke A type cases were the smallest in Group 2, something which indicated that its ANFIS inputs were the most suitable arrangements of clinical indicesin this study. The parameters of Group 2 are MTC, PI, TK, and T1 SPi. The MTC is considered a very effective angle of the scoliosis curve in the frontal plane as well as the PI and TK angles in the sagittal plane. Furthermore, the T1 SPi angle affects the sagittal spinal curve, which can be used as a proper training parameter for the ANFIS algorithm. Hence, the errors in Group 1 increased because T1 Spi was not taken into account. Moreover, the number of inputs in Groups 3 and 4 were greater (i.e., 6 and 7 inputs, respectively); however, the number of scoliotic cases were limited in this study. Therefore, their RMSE and CCDI values increased in those groups as opposed to the corresponding values in Group 2 (Figure. 3).

Differences between predicted and operated results as well as RMSE values were greater in estimating postoperative TK angles. In the majority of cases, the MTC angles were reduced considerably from their preoperative values, for surgeons attempted to decrease the cobb angle as much as possible. Nevertheless, the variation of TK angles did not follow a regular pattern between preoperative and postoperative values in different cases. For instance, four sample cases were analyzed (Figure. 5). The results indicated that the postoperative TK angle could be greater or smaller than its preoperative value. Hence, it is more difficult for the ANFIS algorithm to predict postoperative TK accurately than to predict postoperative MTC accurately (Figure. 4)

Conclusions

The ANFIS algorithm can help estimate and predict postoperative clinical indices, especially when there is a sufficient number of AIS cases. This method can also assist surgeons to estimate postoperative clinical angles in scoliosis correction surgeries (prior to the real operation) and improve the surgical procedure.

According to the results, these errors are often smaller in postoperative MTC estimation than in TK estimation, for the patterns of preoperative and postoperative MTC values are more regular than those of TK values. Therefore, it would be more straightforward for the ANFIS algorithm to train data based on MTC angles

Finally, certain suggestions can be made for future studies. It is recommended to increase the case numbers in a bid to improve the prediction accuracy of postoperative clinical angles in order to reduce estimation errors. Moreover, modeling the spine by considering the effects of soft tissue stiffness in the curvature of scoliosis can improve the process of prediction during a scoliosis surgery. It is also advisable to analyze the rod curvatures in posterior correction surgery of the AIS patients through the ANFIS algorithm with preoperative inputs.

Declarations

Declaration of ethical approval for study: The ethical approval was received from the ethics committee of the Iran University of Medical Sciences (IUMS) for receiving and performing analysis on scoliotic patients' EOS radiographs, under letter no. IR.IUMS.REC.1398.1162, dated 02/22/2020. Therefore, the standards laid down in the Declaration of Helsinki have been adhered to.